Rで線形代数:射影行列

library(ggplot2)

# --- 計算部分 ---
a <- matrix(c(2, 1), ncol = 1)
b <- matrix(c(1, 3), ncol = 1)
P <- (a %*% t(a)) / as.numeric(t(a) %*% a)
p <- P %*% b
e <- b - p

# --- プロット用データの作成 ---

# ベクトル描画用のデータフレーム
df_vectors <- data.frame(
  x_start = c(0, 0, p[1]), y_start = c(0, 0, p[2]),
  x_end = c(b[1], p[1], b[1]), y_end = c(b[2], p[2], b[2]),
  label = c("b (元のベクトル)", "p (射影ベクトル)", "e (誤差ベクトル)")
)

# ラベル表示用のデータフレーム（中点）
df_labels <- data.frame(
  x_pos = c((0 + b[1]) / 2, (0 + p[1]) / 2, (p[1] + b[1]) / 2),
  y_pos = c((0 + b[2]) / 2, (0 + p[2]) / 2, (p[2] + b[2]) / 2),
  label = c("b (元のベクトル)", "p (射影ベクトル)", "e (誤差ベクトル)")
)

# --- プロットの作成 ---
ggplot() +
  # 射影先の部分空間（直線）
  geom_abline(
    intercept = 0, slope = a[2] / a[1],
    color = "skyblue", linetype = "dashed", linewidth = 1
  ) +

  # ベクトルを矢印として描画
  geom_segment(
    data = df_vectors,
    aes(x = x_start, y = y_start, xend = x_end, yend = y_end, color = label),
    arrow = arrow(length = unit(0.3, "cm")),
    linewidth = 1.2
  ) +

  # ラベルを中点に表示
  geom_text(
    data = df_labels,
    aes(x = x_pos, y = y_pos, label = label, color = label),
    hjust = 0.5,
    vjust = -0.7,
    size = 4,
    fontface = "bold",
    show.legend = FALSE # 凡例が重複しないようにテキストの凡例は非表示
  ) +

  # 原点を描画
  geom_point(aes(x = 0, y = 0), size = 3, color = "black") +

  # 色の手動設定
  scale_color_manual(
    name = "ベクトル", # 凡例のタイトル
    values = c("b (元のベクトル)" = "red", "p (射影ベクトル)" = "blue", "e (誤差ベクトル)" = "darkgreen")
  ) +

  # 軸のスケールを1:1に固定
  coord_fixed(ratio = 1) +

  # 軸の範囲を設定
  xlim(-1.5, 3.5) +
  ylim(-0.5, 3.5) +

  # タイトルとラベル
  labs(
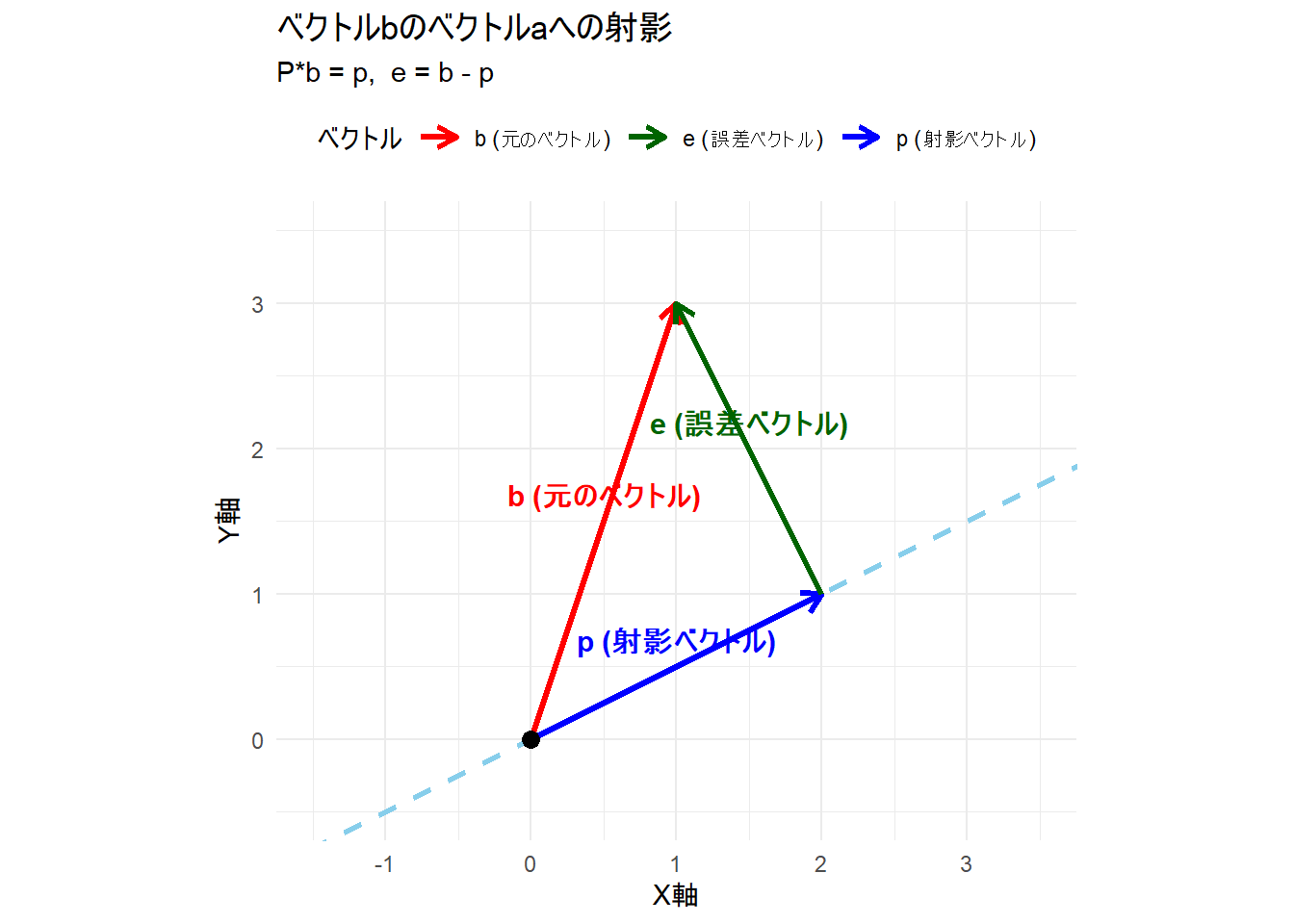
    title = "ベクトルbのベクトルaへの射影",
    subtitle = "P*b = p,  e = b - p",
    x = "X軸",
    y = "Y軸"
  ) +

  # テーマ
  theme_minimal() +
  theme(legend.position = "top")

# --- 1. 計算部分 ---

# 射影先の平面を張るベクトル
a1 <- matrix(c(1, 0, 1), ncol = 1)
a2 <- matrix(c(0, 1, 1), ncol = 1)
# 射影したい元のベクトル
b <- matrix(c(2, 3, 1), ncol = 1)

# 行列 A を作成
A <- cbind(a1, a2)
# 射影行列 P の計算
P <- A %*% solve(t(A) %*% A) %*% t(A)
# ベクトル b を射影して p を計算
p <- P %*% b
# 誤差ベクトル e の計算
e <- b - p


# --- 2. プロット用データ作成 ---

# 3D座標を擬似2D座標に変換する関数
project_3d_to_2d <- function(v, angle = 0.8, z_scale = 0.5) {
  x2d <- v[1] - z_scale * v[3] * cos(angle)
  y2d <- v[2] - z_scale * v[3] * sin(angle)
  return(c(x = x2d, y = y2d))
}

# 1. 射影先の平面グリッド (3D -> 2D)
s <- seq(-1.5, 2.5, by = 0.5)
t <- seq(-1, 3, by = 0.5)
grid_data <- expand.grid(s = s, t = t)
plane_points_3d <- t(apply(grid_data, 1, function(row) row["s"] * a1 + row["t"] * a2))
plane_points_2d_matrix <- t(apply(plane_points_3d, 1, project_3d_to_2d))
df_plane_2d <- as.data.frame(plane_points_2d_matrix)
colnames(df_plane_2d) <- c("x", "y")

# 2. ベクトル描画用のデータ (3D -> 2D)
vec_data_3d <- data.frame(
  x_start = c(0, 0, p[1]), y_start = c(0, 0, p[2]), z_start = c(0, 0, p[3]),
  x_end = c(b[1], p[1], b[1]), y_end = c(b[2], p[2], b[2]), z_end = c(b[3], p[3], b[3]),
  label = c("b (元のベクトル)", "p (射影ベクトル)", "e (誤差ベクトル)")
)
vec_data_2d_matrix <- cbind(
  t(apply(vec_data_3d[, 1:3], 1, project_3d_to_2d)),
  t(apply(vec_data_3d[, 4:6], 1, project_3d_to_2d))
)
vec_data_2d <- as.data.frame(vec_data_2d_matrix)
colnames(vec_data_2d) <- c("x_start", "y_start", "x_end", "y_end")
vec_data_2d$label <- vec_data_3d$label


# 3. ラベル表示用のデータを作成 (3Dの中点を2Dに投影)
# まず、各ベクトルの中点の3D座標を計算
label_pos_3d <- data.frame(
  x_pos = c((0 + b[1]) / 2, (0 + p[1]) / 2, (p[1] + b[1]) / 2),
  y_pos = c((0 + b[2]) / 2, (0 + p[2]) / 2, (p[2] + b[2]) / 2),
  z_pos = c((0 + b[3]) / 2, (0 + p[3]) / 2, (p[3] + b[3]) / 2),
  label = c("b (元のベクトル)", "p (射影ベクトル)", "e (誤差ベクトル)")
)

# 次に、その3D中点座標を2Dに投影
df_labels_2d_matrix <- t(apply(label_pos_3d[, 1:3], 1, project_3d_to_2d))
df_labels_2d <- as.data.frame(df_labels_2d_matrix)
colnames(df_labels_2d) <- c("x", "y")
df_labels_2d$label <- label_pos_3d$label


# --- 3. ggplotによる描画 ---
ggplot() +
  # 射影先の平面をグリッドで描画
  geom_point(data = df_plane_2d, aes(x = x, y = y), color = "black", size = 1) +

  # 座標軸を描画
  geom_segment(aes(x = 0, y = 0, xend = project_3d_to_2d(c(4, 0, 0))["x"], yend = project_3d_to_2d(c(4, 0, 0))["y"]), color = "gray", arrow = arrow(length = unit(0.2, "cm"))) +
  geom_segment(aes(x = 0, y = 0, xend = project_3d_to_2d(c(0, 4, 0))["x"], yend = project_3d_to_2d(c(0, 4, 0))["y"]), color = "gray", arrow = arrow(length = unit(0.2, "cm"))) +
  geom_segment(aes(x = 0, y = 0, xend = project_3d_to_2d(c(0, 0, 4))["x"], yend = project_3d_to_2d(c(0, 0, 4))["y"]), color = "gray", arrow = arrow(length = unit(0.2, "cm"))) +
  geom_text(aes(x = project_3d_to_2d(c(4.2, 0, 0))["x"], y = project_3d_to_2d(c(4.2, 0, 0))["y"]), label = "X", color = "gray") +
  geom_text(aes(x = project_3d_to_2d(c(0, 4.2, 0))["x"], y = project_3d_to_2d(c(0, 4.2, 0))["y"]), label = "Y", color = "gray") +
  geom_text(aes(x = project_3d_to_2d(c(0, 0, 4.2))["x"], y = project_3d_to_2d(c(0, 0, 4.2))["y"]), label = "Z", color = "gray") +

  # 各ベクトルを矢印で描画
  geom_segment(
    data = vec_data_2d,
    aes(x = x_start, y = y_start, xend = x_end, yend = y_end, color = label),
    arrow = arrow(length = unit(0.3, "cm")),
    linewidth = 1.2
  ) +

  # ラベルを各ベクトルの中点に表示
  geom_text(
    data = df_labels_2d,
    aes(x = x, y = y, label = label, color = label),
    hjust = 0.5, # 水平方向中央
    vjust = -0.7, # 少し上にずらす
    size = 4,
    fontface = "bold"
  ) +

  # スケール、テーマ、タイトルの設定
  scale_color_manual(values = c("b (元のベクトル)" = "red", "p (射影ベクトル)" = "blue", "e (誤差ベクトル)" = "darkgreen")) +
  coord_fixed(ratio = 1) +
  theme_void() +
  labs(
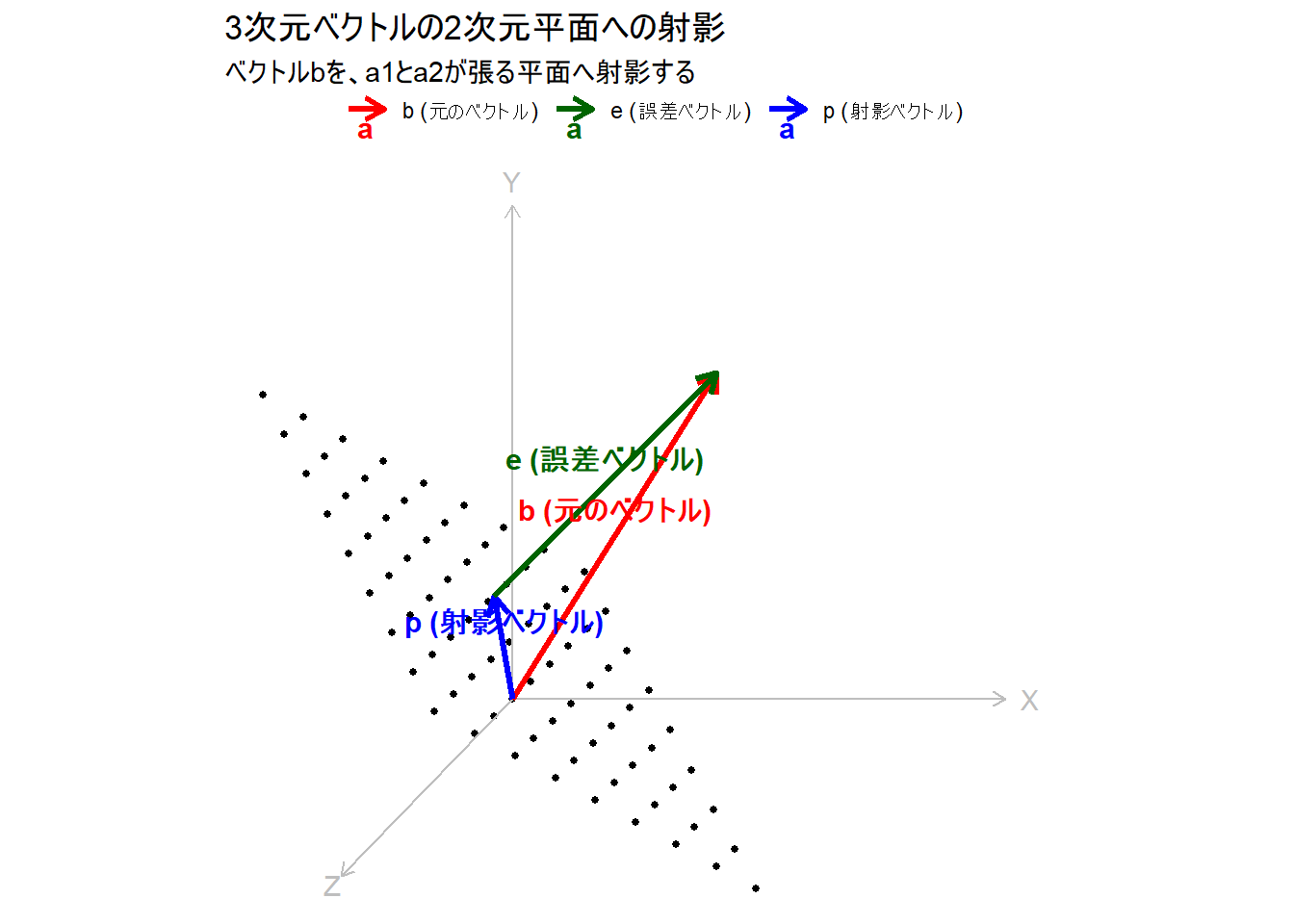
    title = "3次元ベクトルの2次元平面への射影",
    subtitle = "ベクトルbを、a1とa2が張る平面へ射影する",
    color = ""
  ) +
  theme(legend.position = "top")