Rで GARCHモデル を試みます。
1. GARCHモデルとは
GARCH(Generalized Autoregressive Conditional Heteroskedasticity, 一般化自己回帰条件付き分散不均一)モデルは、金融時系列データなどで観測されるボラティリティ・クラスタリング(変動が激しい期間と穏やかな期間がそれぞれ固まって現れる現象)を捉えるモデルです。
まず、GARCHモデルの基礎となるARCH(Autoregressive Conditional Heteroskedasticity)モデルから説明します。
ARCH(q)モデル
時刻\(t\)における資産収益率を\(r_t\)とします。\(r_t\)は期待収益率(平均)\(\mu\)と予測不能な誤差項\(\varepsilon_t\)からなると考えます。
\(r_t = \mu + \varepsilon_t\)
この誤差項\(\varepsilon_t\)は、条件付き標準偏差\(\sigma_t\)と、平均0、分散1のホワイトノイズ\(z_t\)の積で表されます。
\(\varepsilon_t = \sigma_t z_t, \quad z_t \sim N(0, 1)\)
ARCHモデルの前提は、条件付き分散\(\sigma_t^2\)が過去の誤差項(ショック)\(\varepsilon_{t-i}^2\)の大きさに依存するという点にあります。ARCH(q)モデルでは、\(\sigma_t^2\)は以下のように定義されます。
\(\sigma_t^2 = \omega + \sum_{i=1}^{q} \alpha_i \varepsilon_{t-i}^2\)
ここで、
- \(\omega > 0\): 定数項。長期的な平均分散のレベルを示します。
- \(\alpha_i \ge 0\): 過去のショックの2乗\(\varepsilon_{t-i}^2\)が現在のボラティリティに与える影響の大きさを示す係数。
- \(q\): 過去の何期前までのショックを考慮するかを示す次数(ラグ)。
ARCHモデルは、「過去に大きなショック(\(\varepsilon_{t-i}^2\)が大きい)があれば、現在のボラティリティ(\(\sigma_t^2\))も大きくなる」というボラティリティ・クラスタリングを表現できます。
GARCH(p, q)モデル
GARCHモデルは、ARCHモデルをさらに一般化し、条件付き分散\(\sigma_t^2\)が過去の条件付き分散\(\sigma_{t-j}^2\)自体にも依存すると考えます。これにより、長期のボラティリティの持続性を表現できます。
GARCH(p, q)モデルにおける\(\sigma_t^2\)の定義は以下の通りです。
\(\sigma_t^2 = \omega + \sum_{i=1}^{q} \alpha_i \varepsilon_{t-i}^2 + \sum_{j=1}^{p} \beta_j \sigma_{t-j}^2\)
ここで、
- \(\alpha_i\): ARCH項の係数。過去のショックがボラティリティに与える短期的な影響。
- \(\beta_j\): GARCH項の係数。過去のボラティリティが現在のボラティリティに与える影響、つまりボラティリティの持続性を示します。
- \(p\): 過去の何期前までの条件付き分散を考慮するかを示す次数。
- \(q\): 過去の何期前までのショックを考慮するかを示す次数。
具体例として、GARCH(1,1)モデル は以下の通りのモデルになります。
\(\sigma_t^2 = \omega + \alpha_1 \varepsilon_{t-1}^2 + \beta_1 \sigma_{t-1}^2\)
制約条件:
- \(\omega > 0, \alpha_1 \ge 0, \beta_1 \ge 0\): 分散が負にならないための条件。
- \(\alpha_1 + \beta_1 < 1\): モデルが定常(ボラティリティが時間とともに発散しない)であるための条件。この条件が満たされるとき、長期的な平均分散は \(\frac{\omega}{1 - \alpha_1 - \beta_1}\) に収束します。
\(\alpha_1 + \beta_1\)の値が1に近いほど、ボラティリティの持続性が高く、ショックの影響が長く残ることを意味します。
それでは、この理論に基づいてシミュレーションを開始します。
以降、有意水準は 5% とします
シミュレーションの準備
まず、必要なパッケージを読み込みます。
# パッケージの読み込み
library(rugarch)
library(ggplot2)
library(tidyr)
options(scipen = 999)
seed <- 202507122. サンプル時系列データの作成
GARCH(1,1)モデルに従う時系列データを手動で作成します。
# シミュレーションの設定
set.seed(seed) # 結果の再現性のため乱数シードを固定
n <- 2000 # データ点の数
# GARCH(1,1)モデルの「真の」パラメータを設定
mu <- 0.0005 # 平均リターン
omega <- 0.00001 # ω
alpha1 <- 0.10 # α1
beta1 <- 0.85 # β1
# 定常性の確認 (α1 + β1 < 1)
cat("--- 定常性の確認 ---\n\n")
cat(paste0("α1 + β1 = ", alpha1 + beta1, " (< 1 であれば定常)\n"))
# 結果を格納するベクトルを初期化
r <- numeric(n) # リターン
epsilon <- numeric(n) # 誤差項
sigma2 <- numeric(n) # 条件付き分散
# 初期値の設定 (長期的な平均分散)
sigma2[1] <- omega / (1 - alpha1 - beta1)
epsilon[1] <- sqrt(sigma2[1]) * rnorm(1)
r[1] <- mu + epsilon[1]
# GARCH(1,1)プロセスのシミュレーション
for (t in 2:n) {
# 1. 前期の値を用いて、当期の条件付き分散を計算
sigma2[t] <- omega + alpha1 * epsilon[t - 1]^2 + beta1 * sigma2[t - 1]
# 2. 当期の誤差項を生成
epsilon[t] <- sqrt(sigma2[t]) * rnorm(1)
# 3. 当期のリターンを計算
r[t] <- mu + epsilon[t]
}
# 作成したデータをデータフレームに格納
sim_data <- data.frame(
time = 1:n,
returns = r,
true_sigma = sqrt(sigma2)
)
cat("\n--- サンプル時系列データの一部を確認: ---\n\n")
print(head(sim_data, 10))--- 定常性の確認 ---
α1 + β1 = 0.95 (< 1 であれば定常)
--- サンプル時系列データの一部を確認: ---
time returns true_sigma
1 1 -0.015485124 0.01414214
2 2 -0.012417777 0.01433710
3 3 -0.007423762 0.01419177
4 4 -0.038560444 0.01369212
5 5 0.030775493 0.01794226
6 6 -0.008236653 0.01937257
7 7 -0.013103697 0.01834762
8 8 -0.001068541 0.01773826
9 9 0.008991248 0.01666418
10 10 0.010061244 0.015913863. パッケージrugarchを利用してモデルを推定
次に、作成したサンプルデータrを用いて、rugarchパッケージでGARCH(1,1)モデルを推定します。
ugarchfit関数の引数と結果の説明
ugarchfit関数は、指定されたGARCHモデルをデータに適合させるための関数です。その前に、ugarchspecでモデルの構造を定義する必要があります。
ugarchspecの主な引数:
-
variance.model: 分散モデルの仕様をリストで指定します。-
model: GARCHの種類(例: “sGARCH”は標準GARCH)。 -
garchOrder:c(p, q)の形式でGARCHの次数を指定。
-
-
mean.model: 平均モデルの仕様をリストで指定します。-
armaOrder: ARMAモデルの次数c(ar, ma)。今回はc(0, 0)。 -
include.mean: 定数項muをモデルに含めるかどうか。
-
-
distribution.model: 誤差項の分布(例: “norm”は正規分布)。
ugarchfitの主な引数:
-
spec:ugarchspecで作成したモデル仕様オブジェクト。 -
data: 当てはめる対象の時系列データ。 -
solver: 最尤推定を行うための最適化ソルバー。
ugarchfitの結果 (uGARCHfitオブジェクト):
このオブジェクトはS4クラスであり、@記号を使って各スロットにアクセスします。
-
@fit$coef: 推定されたモデルの係数ベクトル。 -
@fit$matcoef: 係数、標準誤差、t値、p値を含む行列。モデルの妥当性評価に利用。 -
@fit$sigma: 推定された条件付き標準偏差の時系列。 -
@fit$residuals: リターンから平均を引いた誤差項。 -
@fit$z: 標準化残差(\(\varepsilon_t / \sigma_t\))。これがホワイトノイズになっているかを確認します。
# 1. モデルの仕様を定義
# GARCH(1,1)モデル、平均は定数項のみ、誤差項は正規分布
spec <- ugarchspec(
variance.model = list(model = "sGARCH", garchOrder = c(1, 1)),
mean.model = list(armaOrder = c(0, 0), include.mean = TRUE),
distribution.model = "norm"
)
# 2. モデルの推定
# dataにはベクトル形式のrを渡す
garch_fit <- ugarchfit(spec = spec, data = r)
# 3. 推定結果のサマリーを表示
cat("--- GARCHモデルの推定結果 ---\n")
print(garch_fit)--- GARCHモデルの推定結果 ---
*---------------------------------*
* GARCH Model Fit *
*---------------------------------*
Conditional Variance Dynamics
-----------------------------------
GARCH Model : sGARCH(1,1)
Mean Model : ARFIMA(0,0,0)
Distribution : norm
Optimal Parameters
------------------------------------
Estimate Std. Error t value Pr(>|t|)
mu 0.000796 0.000281 2.8312 0.004637
omega 0.000008 0.000001 7.1198 0.000000
alpha1 0.106113 0.007952 13.3434 0.000000
beta1 0.854409 0.011961 71.4301 0.000000
Robust Standard Errors:
Estimate Std. Error t value Pr(>|t|)
mu 0.000796 0.000273 2.9168 0.003537
omega 0.000008 0.000001 6.3921 0.000000
alpha1 0.106113 0.005902 17.9778 0.000000
beta1 0.854409 0.009317 91.7002 0.000000
LogLikelihood : 5741.416
Information Criteria
------------------------------------
Akaike -5.7374
Bayes -5.7262
Shibata -5.7374
Hannan-Quinn -5.7333
Weighted Ljung-Box Test on Standardized Residuals
------------------------------------
statistic p-value
Lag[1] 0.02458 0.8754
Lag[2*(p+q)+(p+q)-1][2] 0.52446 0.6822
Lag[4*(p+q)+(p+q)-1][5] 2.00634 0.6169
d.o.f=0
H0 : No serial correlation
Weighted Ljung-Box Test on Standardized Squared Residuals
------------------------------------
statistic p-value
Lag[1] 1.025 0.3113
Lag[2*(p+q)+(p+q)-1][5] 1.700 0.6907
Lag[4*(p+q)+(p+q)-1][9] 4.508 0.5051
d.o.f=2
Weighted ARCH LM Tests
------------------------------------
Statistic Shape Scale P-Value
ARCH Lag[3] 0.244 0.500 2.000 0.6213
ARCH Lag[5] 1.663 1.440 1.667 0.5506
ARCH Lag[7] 3.657 2.315 1.543 0.3988
Nyblom stability test
------------------------------------
Joint Statistic: 20.1466
Individual Statistics:
mu 0.30637
omega 2.69669
alpha1 0.07589
beta1 0.04329
Asymptotic Critical Values (10% 5% 1%)
Joint Statistic: 1.07 1.24 1.6
Individual Statistic: 0.35 0.47 0.75
Sign Bias Test
------------------------------------
t-value prob sig
Sign Bias 0.8556 0.3923
Negative Sign Bias 1.2579 0.2086
Positive Sign Bias 0.3510 0.7256
Joint Effect 1.7063 0.6355
Adjusted Pearson Goodness-of-Fit Test:
------------------------------------
group statistic p-value(g-1)
1 20 13.58 0.8076
2 30 16.90 0.9637
3 40 23.24 0.9786
4 50 26.95 0.9956
Elapsed time : 0.2553229 GARCHモデル推定結果の解説
出力は大きく分けて、(1)モデルの仕様、(2)推定されたパラメータ、(3)モデルの適合度、(4)残差の診断的検定の4つのセクションから構成されています。
1. モデルの基本情報 (Conditional Variance Dynamics)
GARCH Model : sGARCH(1,1)
Mean Model : ARFIMA(0,0,0)
Distribution : norm - GARCH Model: sGARCH(1,1)
-
sGARCHは標準GARCH(Standard GARCH)モデルを使用したことを意味します。 -
(1,1)は、分散のダイナミクスをモデル化する際に、過去1期分のショック(ARCH項)と過去1期分の分散(GARCH項)を使用するGARCH(p=1, q=1)モデルであることを示しています。
-
- Mean Model: ARFIMA(0,0,0)
- これはリターンの平均部分のモデルです。
ARFIMA(0,0,0)かつinclude.mean = TRUE(コードで指定)の場合、モデルは単純な定数項(平均リターン)のみを持つことを意味します。数式で表すと \(r_t = \mu + \varepsilon_t\) となります。
- これはリターンの平均部分のモデルです。
- Distribution: norm
- モデルの誤差項(標準化残差 \(z_t\))が正規分布(normal distribution)に従うと仮定して推定されたことを示します。
2. 推定されたパラメータ (Optimal Parameters / Robust Standard Errors)
Optimal Parameters
------------------------------------
Estimate Std. Error t value Pr(>|t|)
mu 0.000796 0.000281 2.8312 0.004637
omega 0.000008 0.000001 7.1198 0.000000
alpha1 0.106113 0.007952 13.3434 0.000000
beta1 0.854409 0.011961 71.4301 0.000000-
Estimate: 各パラメータの推定値。 -
Std. Error: 標準誤差。推定値の不確実性(ばらつき)を示します。 -
t value: t値 (Estimate/Std. Error)。パラメータが0と有意に異なるかを検定するための統計量。 -
Pr(>|t|): p値。設定した有意水準未満であれば「統計的に有意」と判断し、モデルにとって必要なパラメータであると考えます。
各パラメータの解釈は以下の通りです。
-
mu: 平均リターン(\(\mu\))の推定値。0.000796。p値が0.0046と設定した有意水準を下回っています。 -
omega: 分散方程式の定数項(\(\omega\))の推定値。0.000008。p値が設定した有意水準を下回っています。 -
alpha1: ARCH項の係数(\(\alpha_1\))の推定値。0.106113。過去のショック(サプライズ)が現在のボラティリティに与える影響の大きさを示します。p値が設定した有意水準を下回っています。 -
beta1: GARCH項の係数(\(\beta_1\))の推定値。0.854409。過去のボラティリティが現在のボラティリティに与える影響の大きさ、つまりボラティリティの持続性を示します。p値が設定した有意水準を下回っています。
示唆:
- ボラティリティの持続性:
alpha1 + beta1= 0.106 + 0.854 = 0.96。この値が1に近いほど、一度発生したボラティリティの変動が長く持続することを示します。0.96は1に近く、高い持続性があることがわかります。 -
Robust Standard Errorsは、モデルの仮定が完全に満たされない場合でも一致性を持つ標準誤差です。こちらのp値を見ても、全てのパラメータが設定した有意水準を下回っています。
3. モデルの適合度 (LogLikelihood / Information Criteria)
-
LogLikelihood(対数尤度): 5741.416。この値自体に直接的な意味はありませんが、異なるモデルを比較する際の基準となります(値が大きいほど適合が良い)。 -
Information Criteria(情報量規準): Akaike (AIC), Bayes (BIC)など。モデルの適合度と複雑さ(パラメータ数)のバランスを評価する指標です。異なるモデルを比較する際に値が小さい方を選択します。
4. 残差の診断的検定 (各種検定)
このセクションは、推定されたモデルがデータをうまく説明できているか(モデルの仮定が満たされているか)を検証します。良いモデルであれば、残差から全てのパターン(自己相関やボラティリティのクラスタリング)が取り除かれているはずです。
- Weighted Ljung-Box Test on Standardized Residuals (標準化残差のLjung-Box検定)
- 目的: 平均モデルの残差 (\(\varepsilon_t / \sigma_t\)) に自己相関が残っていないかを検定します。
- 帰無仮説 (H0): 「自己相関はない」。
- 結果: p値が全て設定した有意水準を上回っているため、帰無仮説を棄却できません。よって、平均モデルがリターンの自己相関をうまく捉えられていることを示唆します。
- Weighted Ljung-Box Test on Standardized Squared Residuals (標準化残差の2乗のLjung-Box検定)
- 目的: ボラティリティを取り除いた後の残差の2乗に、ボラティリティ・クラスタリング(ARCH効果)が残っていないかを検定します。
- 帰無仮説 (H0): 「ARCH効果はない」。
- 結果: p値が全て設定した有意水準を上回っているため、帰無仮説を棄却できません。よって、GARCH(1,1)モデルがデータのボラティリティ構造をうまく捉えきったことを示唆します。
- Weighted ARCH LM Tests (ARCH-LM検定)
- 目的: 上記の検定と同様に、残差にARCH効果が残っていないかを検定する別の手法です。
- 帰無仮説 (H0): 「ARCH効果はない」。
- 結果: P値が全て設定した有意水準を上回っているため、帰無仮説を棄却できません。よって、モデルがボラティリティを適切にモデル化できていることを示唆します。
- Nyblom stability test (Nyblom安定性検定)
- 目的: 推定されたパラメータが、分析期間を通じて安定的であったかを検定します。
- 帰無仮説 (H0): 「パラメータは安定的である」。
- 結果:
Joint Statistic(20.14)が臨界値(5%で1.24)を上回っているため、帰無仮説は棄却されます。これは、パラメータが期間中に変動した可能性を示唆します(棄却されますが、今回のシミュレーションではこのまま先に進みます)。
| 検定方法 | ルール | 結論 |
|---|---|---|
| 臨界値による検定 | 検定統計量 > 臨界値 | 帰無仮説を棄却 |
| p値による検定 | p値 < 有意水準 | 帰無仮説を棄却 |
- Sign Bias Test (符号バイアス検定)
- 目的: ポジティブなショックとネガティブなショックが、ボラティリティに非対称な影響(レバレッジ効果)を与えていないかを検定します。
- 帰無仮説 (H0): 「非対称な効果(符号バイアス)はない」。
- 結果: 全てのp値(
prob)が設定した有意水準を上回っているため、帰無仮説を棄却できません。よって、レバレッジ効果を考慮しない標準GARCHモデルで十分であることを示唆します。
- Adjusted Pearson Goodness-of-Fit Test (適合度検定)
- 目的: モデルで仮定した分布(今回は正規分布)が、実際のデータの分布にどれだけ適合しているかを検定します。
- 帰無仮説 (H0): 「データは仮定された分布に従う」。
- 結果: p値が全て設定した有意水準を上回っているため、帰無仮説を棄却できません。よっt、残差が正規分布に従うという仮定が妥当であったことを示唆します。
4. 推定したモデルの係数とサンプルデータ作成に利用した係数を比較
シミュレーションがうまく機能していれば、garch_fitによって推定された係数は、ステップ2で設定した「真の」係数に近いはずです。
# 真のパラメータ
true_params <- c(mu = mu, omega = omega, alpha1 = alpha1, beta1 = beta1)
# 推定されたパラメータ
est_params <- coef(garch_fit)
# 比較用のデータフレームを作成
comparison_df <- data.frame(
パラメータ = names(true_params),
真の値 = true_params,
推定値 = round(est_params, 5),
row.names = NULL
)
cat("--- 真の係数と推定された係数の比較 ---\n\n")
print(comparison_df)--- 真の係数と推定された係数の比較 ---
パラメータ 真の値 推定値
1 mu 0.00050 0.00080
2 omega 0.00001 0.00001
3 alpha1 0.10000 0.10611
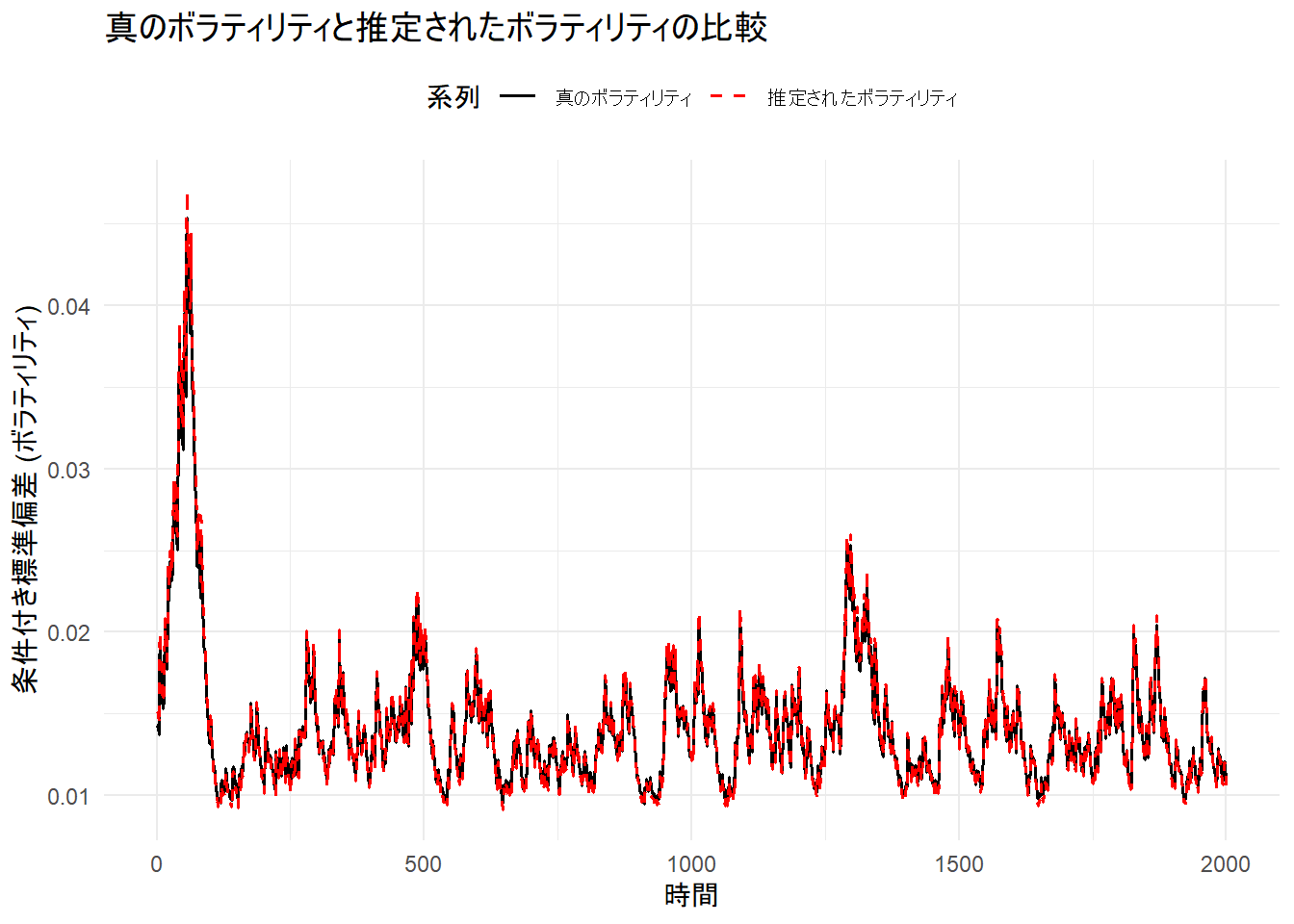
4 beta1 0.85000 0.85441推定された係数は、シミュレーションで設定した真の値に近いことが確認できます(但し、Nyblom stability test は棄却されています)。
5. プロットの作成
最後に、シミュレーションで生成した「真の」ボラティリティと、rugarchが推定したボラティリティを比較するプロットを作成します。
# rugarchの結果から推定された条件付き標準偏差を取得
est_sigma <- sigma(garch_fit)
# プロット用にデータを整形
plot_data <- data.frame(
time = 1:n,
真のボラティリティ = sim_data$true_sigma,
推定されたボラティリティ = as.numeric(est_sigma)
)
# データをロングフォーマットに変換
plot_data_long <- pivot_longer(
plot_data,
cols = c("真のボラティリティ", "推定されたボラティリティ"),
names_to = "系列",
values_to = "ボラティリティ"
)
# プロットを作成
p_volatility <- ggplot(plot_data_long, aes(x = time, y = ボラティリティ, color = 系列, linetype = 系列)) +
geom_line(linewidth = 0.6) +
scale_color_manual(values = c("真のボラティリティ" = "black", "推定されたボラティリティ" = "red")) +
scale_linetype_manual(values = c("真のボラティリティ" = "solid", "推定されたボラティリティ" = "dashed")) +
labs(
title = "真のボラティリティと推定されたボラティリティの比較",
x = "時間",
y = "条件付き標準偏差 (ボラティリティ)",
color = "系列",
linetype = "系列"
) +
theme_minimal() +
theme(legend.position = "top")
print(p_volatility)以上です。