RでGLMM 誤差構造:二項分布、リンク関数:logit

Rで 誤差構造 を 二項分布、リンク関数 を logit とする 一般化線形混合モデル(GLMM) を試みます。

1. シミュレーションのシナリオ設定

【シナリオ：新開発の農薬の効果検証】

ある製薬会社が、作物を特定の病気から守るための新しい農薬Aを開発しました。この新農薬Aが、現在広く使われている従来農薬Bよりも効果が高いかを検証するための大規模な実地試験を行うことにしました。

目的: 新農薬Aは従来農薬Bよりも病気の発生を抑える効果があるか？
実験計画:
- 地域の15軒の農家（farmer）に協力してもらい、試験を実施します。
- 各農家は、自分の畑を20区画に分けます。
- ランダムに10区画には新農薬Aを、残りの10区画には従来農薬Bを散布します。
- 検定の有意水準は5%とします。
データ収集:
- 収穫期に、各区画の作物が病気を発症したか否か（1: 発症, 0: 健康）を記録します。
統計モデル: 誤差構造を二項分布、リンク関数をlogitとする一般化線形混合モデルを利用します。理由は以下の通りです。
1. 応答変数の性質: 結果は「発病(1)/健康(0)」の二値データであるため、誤差構造に二項分布を仮定するモデルが適切です。
2. データの非独立性: 今回のデータは「区画」が「農家」に属するという階層構造を持っています。同じ農家内の区画は、土壌や管理方法といった共通の環境要因の影響を受けるため、データが完全に独立であるとは言えません(クラスター効果)。
3. 非独立性を無視する問題点: もしこの農家ごとのばらつきを無視して、全てのデータが独立であるかのようにGLM（glm(disease ~ treatment, family = binomial)）で分析した場合、農薬の効果（treatment）の標準誤差を過小評価してしまいます。よって、農家ごとのばらつきを変量効果（ランダム効果）としてモデルに組み込み、各観測値が独立でないことを考慮することにより、農家差を差し引いた上で、純粋な農薬の効果(固定効果)を推定、評価できます。
考慮すべき点:
- 固定効果: 検証したい要因は「農薬の種類（treatment）」です。これが病気の発症確率にどう影響するかを見たいので、固定効果として扱います。
- 変量効果: しかし、農家ごとに土壌の質、日当たり、水はけ、普段の管理の丁寧さなどは様々です。これらの「農家ごとの環境差」によって、病気の発生しやすさのベースラインが農家ごとに異なると考えられます。この観測値間の非独立性（同じ農家の区画はデータが似通う）を考慮するため、「農家（farmer）」を変量効果としてモデルに組み込みます。

2. R言語によるシミュレーション

上記のシナリオに沿って、Rでデータを生成し、lme4パッケージのglmer関数を使ってGLMMのフィッティングを行います。

2.1. 準備

必要なパッケージを読み込みます。

# パッケージの読み込み
library(lme4)
library(tidyverse)

2.2. データ生成

シナリオに基づいて、パラメータを設定し、シミュレーションデータを作成します。

seed <- 20250702
set.seed(seed)

# 1. パラメータ設定
n_farmers <- 15 # 農家の数
n_plots_per_farmer <- 20 # 各農家の区画数
N <- n_farmers * n_plots_per_farmer # 総データ数

# 固定効果のパラメータ (ロジットスケール)
beta_0 <- 1.2 # 切片: 従来農薬Bでの平均的な発病しやすさ

beta_1 <- -2.0 # 農薬の効果: 新農薬Aは発病しやすさを下げる

# 変量効果のパラメータ
# 農家ごとの切片のばらつき（標準偏差）
sigma_farmer <- 1.5

# 2. 変量効果の生成
# 各農家に対するランダムな切片効果を生成 (平均0, 標準偏差sigma_farmerの正規分布に従う)
random_effects_farmer <- rnorm(n_farmers, mean = 0, sd = sigma_farmer)

# 3. データフレームの作成
sim_data <- tibble(
  # 農家ID (1~15)
  farmer = factor(rep(1:n_farmers, each = n_plots_per_farmer)),

  # 農薬の種類 (各農家でAとBを10区画ずつ)
  treatment = rep(rep(c("B_従来薬", "A_新農薬"), each = 10), times = n_farmers)
) %>%
  # 扱いやすいようにダミー変数化 (A_新農薬 = 1, B_従来薬 = 0)
  mutate(treatment_dummy = if_else(treatment == "A_新農薬", 1, 0)) %>%
  # 各農家の変量効果をデータに割り当て
  mutate(farmer_effect = random_effects_farmer[as.numeric(farmer)])


# 4. 応答変数の生成
# 線形予測子 (η) = 固定効果 + 変量効果
sim_data <- sim_data %>%
  mutate(
    eta = beta_0 + beta_1 * treatment_dummy + farmer_effect,
    # ロジットの逆関数で確率 (p) に変換
    prob = 1 / (1 + exp(-eta)),
    # 確率pに基づき、二項分布から発病(1)か健康(0)を生成
    disease = rbinom(N, size = 1, prob = prob)
  )

sim_data <- sim_data %>%
  mutate(treatment = factor(treatment, levels = c("B_従来薬", "A_新農薬")))

# 確認
# levels(sim_data$treatment)

cat("--- 生成したデータの一部を確認 ---\n")
head(sim_data)

--- 生成したデータの一部を確認 ---
# A tibble: 6 × 7
  farmer treatment treatment_dummy farmer_effect   eta  prob disease
  <fct>  <fct>               <dbl>         <dbl> <dbl> <dbl>   <int>
1 1      B_従来薬                0          1.68  2.88 0.947       1
2 1      B_従来薬                0          1.68  2.88 0.947       1
3 1      B_従来薬                0          1.68  2.88 0.947       1
4 1      B_従来薬                0          1.68  2.88 0.947       1
5 1      B_従来薬                0          1.68  2.88 0.947       1
6 1      B_従来薬                0          1.68  2.88 0.947       1

2.3. GLMMによるモデル推定

生成したデータを使って、GLMMをあてはめます。モデル式は 応答変数 ~ 固定効果 + (1 | 変量効果) のように記述します。(1 | farmer) は、farmer ごとに切片が異なる（ランダム切片）ことを意味します。

# GLMMの実行
# family = binomial(link = "logit") はデフォルトなので省略可能
glmm_model <- glmer(disease ~ treatment + (1 | farmer),
  data = sim_data,
  family = binomial(link = "logit")
)

cat("--- 結果の要約 ---\n")
summary(glmm_model)

--- 結果の要約 ---
Generalized linear mixed model fit by maximum likelihood (Laplace
  Approximation) [glmerMod]
 Family: binomial  ( logit )
Formula: disease ~ treatment + (1 | farmer)
   Data: sim_data

     AIC      BIC   logLik deviance df.resid 
   330.3    341.5   -162.2    324.3      297 

Scaled residuals: 
    Min      1Q  Median      3Q     Max 
-3.4864 -0.5342  0.2119  0.6596  2.6536 

Random effects:
 Groups Name        Variance Std.Dev.
 farmer (Intercept) 1.783    1.335   
Number of obs: 300, groups:  farmer, 15

Fixed effects:
                  Estimate Std. Error z value Pr(>|z|)    
(Intercept)         1.1675     0.4087   2.856  0.00428 ** 
treatmentA_新農薬  -2.0863     0.3154  -6.615 3.73e-11 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Correlation of Fixed Effects:
               (Intr)
trtmntA_新農薬 -0.403

結果の解釈:

Random effects:
- farmer の Std.Dev. (標準偏差) は 1.335 と推定されました。データ生成時の設定は sigma_farmer = 1.5 ですので、農家間のばらつきを捉えられていることを示唆します。
Fixed effects:
- (Intercept) (切片) は 1.1675。と推定されました。データ生成時の設定は beta_0 = 1.2 ですので、従来農薬Bの平均的な発病しやすさ（ロジットスケール）を捉えていることを示唆します。
- treatmentA_新農薬 は -2.0863 と推定されました。データ生成時の設定は beta_1 = -2.0 です。負の値ですので、新農薬Aは従来農薬Bに比べて発病の対数オッズを 約2.09 下げる効果があることを意味します。
なお、(Intercept) のp値が有意水準を超えている場合の「切片（対数オッズ）が0」とは、
- 対数オッズ log(p / (1-p)) = 0
- これを解くと、オッズ p / (1-p) = e⁰ = 1
- さらにこれを解くと、確率 p = 0.5 (つまり50%)
と、「従来農薬Bを使った場合の発病確率は、統計的に50%と区別がつかない」と示唆していることになります。

3. ggplotによる可視化

シミュレーションデータとモデルの推定結果をグラフで可視化し、理解を深めます。

3.1. データの可視化：農家ごとの発病率

まず、農家ごと・農薬ごとに、観測された発病率がどのようになっているかを確認します。

# 農家ごと・農薬ごとの平均発病率を計算
plot_data_summary <- sim_data %>%
  group_by(farmer, treatment) %>%
  summarise(mean_disease = mean(disease), .groups = "drop")

# グラフ化
ggplot(plot_data_summary, aes(x = treatment, y = mean_disease, group = farmer, color = farmer)) +
  geom_line(alpha = 0.8) +
  geom_point(size = 3) +
  labs(
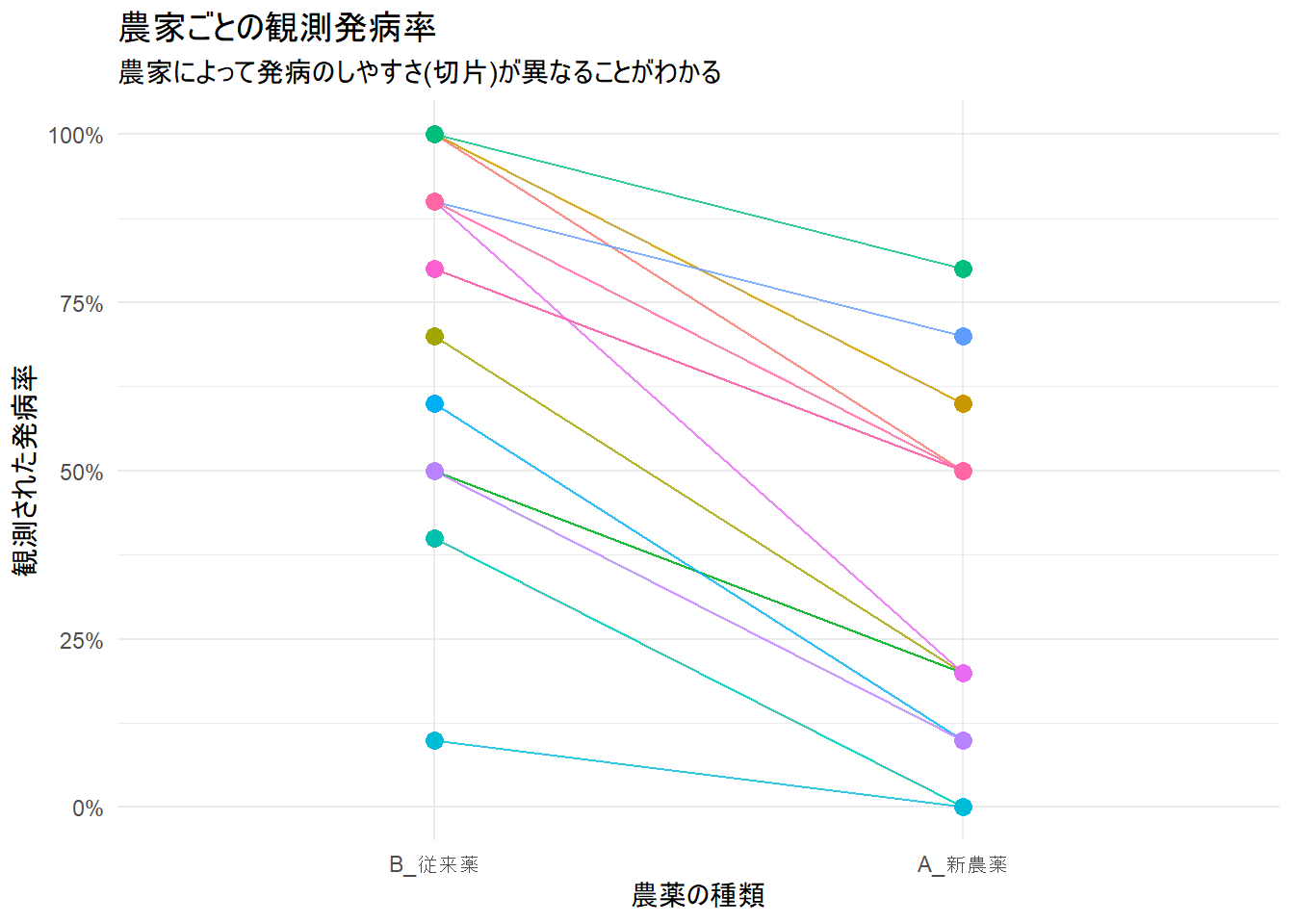
    title = "農家ごとの観測発病率",
    subtitle = "農家によって発病のしやすさ(切片)が異なることがわかる",
    x = "農薬の種類",
    y = "観測された発病率"
  ) +
  scale_y_continuous(labels = scales::percent) +
  theme_minimal() +
  theme(legend.position = "none")

Figure 1 から、ほとんどの農家で新農薬A（右側）の方が発病率が低い傾向が見られます。同時に、線の高さ（切片）が農家ごとに異なっており、これが変量効果として捉えられた「農家差」に相当します。

3.2. モデルによる予測値の可視化

次に、GLMMが各農家に対してどのように発病確率を予測しているかを可視化します。

# モデルから予測確率を取得
sim_data$predicted_prob <- predict(glmm_model, type = "response")

# グラフ化
ggplot(sim_data, aes(x = treatment, y = predicted_prob, group = farmer, color = farmer)) +
  geom_line(alpha = 0.8) +
  geom_point(size = 2) +
  labs(
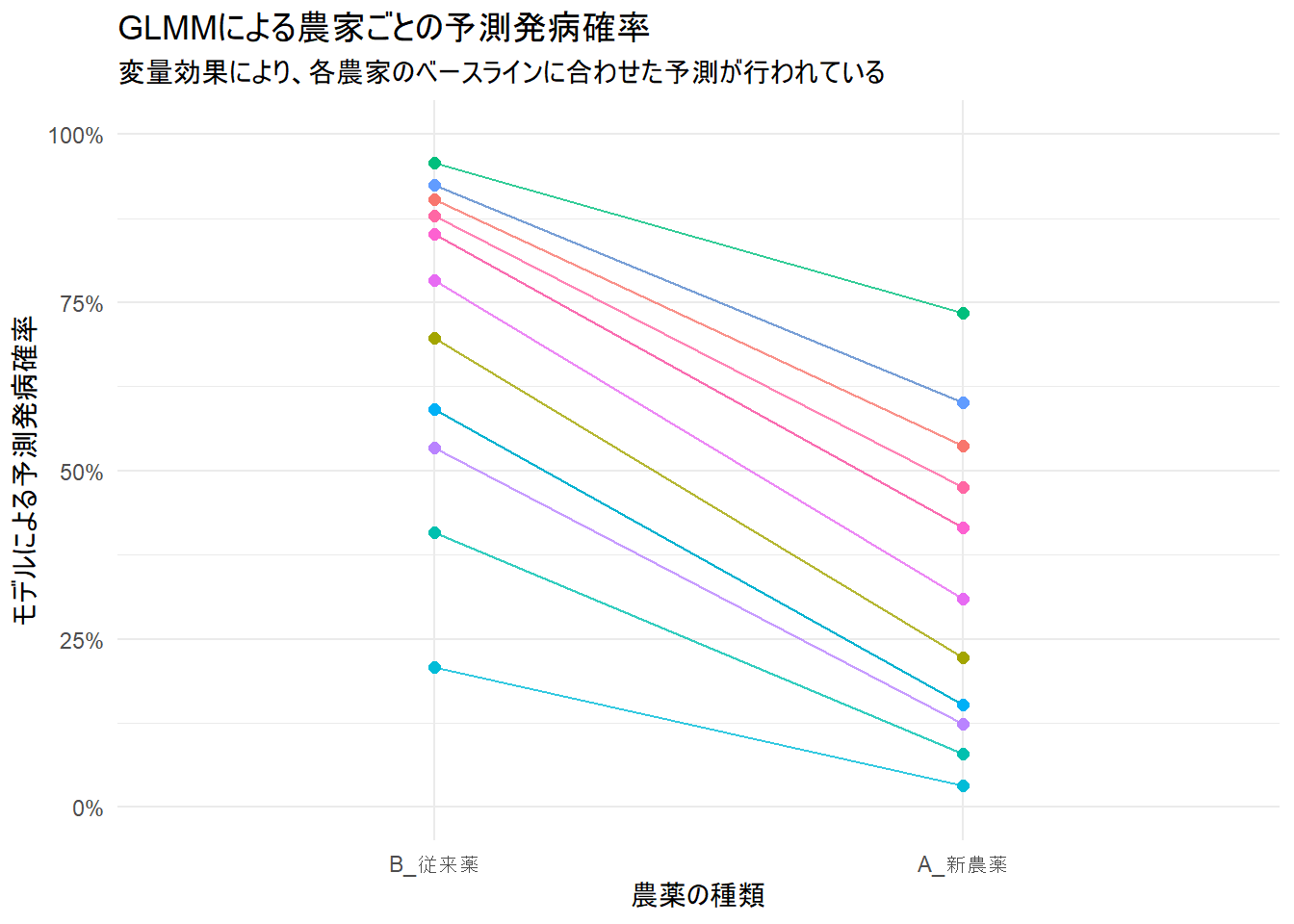
    title = "GLMMによる農家ごとの予測発病確率",
    subtitle = "変量効果により、各農家のベースラインに合わせた予測が行われている",
    x = "農薬の種類",
    y = "モデルによる予測発病確率"
  ) +
  scale_y_continuous(labels = scales::percent, limits = c(0, 1)) +
  theme_minimal() +
  theme(legend.position = "none")

Figure 2 は、モデルが農家ごとのばらつきを捉えていることを示しています。各線の傾きは共通の固定効果 treatment に基づいていますが(確率スケールで見ていますので傾きは異なります)、切片が農家ごとに異なっています。これが、GLMMが「農家差（変量効果）」を考慮しながら「農薬の効果（固定効果）」を推定している様子を視覚的に表現しています。

以上です。