Rで ROC曲線 を試みます。
1. ROC曲線とは
ROC曲線(Receiver Operating Characteristic curve、受信者操作特性曲線)は、2値分類モデルの性能を評価するためのグラフです。分類器が「陽性(Positive)」か「陰性(Negative)」かを予測する際に、その識別能力を視覚的に表現します。
2値分類の混同行列
モデルの予測結果と実際の値を比較すると、以下の4つのケースに分類できます。これをまとめた表を「混同行列(Confusion Matrix)」と呼びます。
| 予測:陽性 | 予測:陰性 | |
|---|---|---|
| 実際:陽性 | 真陽性 (True Positive, TP) | 偽陰性 (False Negative, FN) |
| 実際:陰性 | 偽陽性 (False Positive, FP) | 真陰性 (True Negative, TN) |
ROC曲線の構成要素
ROC曲線は、横軸に偽陽性率 (False Positive Rate, FPR)、縦軸に真陽性率 (True Positive Rate, TPR) をとってプロットした曲線です。
真陽性率 (TPR) / 感度 (Sensitivity) 実際に陽性であるもののうち、正しく「陽性」と予測されたものの割合です。この値が高いほど、陽性のケースを見逃しにくいことを意味します。 \[
TPR = \dfrac{TP}{TP + FN}
\]偽陽性率 (FPR) / (1 - 特異度) 実際に陰性であるもののうち、誤って「陽性」と予測されたものの割合です。この値が低いほど、陰性のケースを誤判定しにくいことを意味します。 \[
FPR = \dfrac{FP}{FP + TN}
\]
ROC曲線の作成方法
多くの分類モデルは、対象が陽性である確率(スコア)を0から1の値で出力します。このスコアに対して「しきい値(threshold)」を設定し、スコアがしきい値以上なら「陽性」、未満なら「陰性」と判定します。
ROC曲線は、このしきい値を0から1まで連続的に変化させたときの、(FPR, TPR) の値のペアをプロットして作成されます。
- しきい値が低い場合: 多くのサンプルが「陽性」と判定されるため、TPRは高くなりますが、同時にFPRも高くなります(曲線右上にプロット)。
- しきい値が高い場合: ほとんどのサンプルが「陰性」と判定されるため、FPRは低くなりますが、同時にTPRも低くなります(曲線左下にプロット)。
ROC曲線の解釈
- 左上への張り出し: 曲線がグラフの左上(FPRが0、TPRが1の点)に近づくほど、モデルの性能が良いことを示します。
- 対角線: (0,0)から(1,1)への対角線は、ランダムに分類した場合の性能を示します。ROC曲線がこの線より上にあれば、モデルはランダムより良い性能を持つと言えます。
- AUC (Area Under the Curve): ROC曲線の下側の面積です。0から1の値をとり、1に近いほど性能が良いことを示す包括的な指標です。AUCが0.5ならランダムな予測と同じ性能、1なら完璧な予測を意味します。
2. シミュレーションのシナリオ
シナリオ:新開発の「がん早期発見マーカー」の性能評価
ある製薬会社が、血液検査で特定のがんを早期発見できる新しい検査薬(マーカー)を開発しました。このマーカーは、血液中の特定物質の濃度を測定し、その数値が高いほど、がんである可能性が高いとされています。
この新しいマーカーが、どれほど正確に「がん患者」と「健康な人」を区別できるかを評価するために、ROC曲線を用いることにしました。
シミュレーションの設定:
- 被験者:
- がん患者群: 150人
- 健康者群: 150人
- データ:
- 両群の被験者から採血し、マーカーの数値を測定します。
- 健康な人のマーカー数値は、平均50、標準偏差10の正規分布に従うと仮定します。
- がん患者のマーカー数値は、平均70、標準偏差15の正規分布に従うと仮定します。
- 2つのグループの分布には「重なり」があり、この重なりの部分をいかに上手く分類するかが、このマーカーの性能の鍵となります。
- 目的: マーカー数値の「しきい値」をいくつに設定すれば陽性と判定するのが最適か、その判断材料としてROC曲線を作成し、この検査の総合的な性能をAUCで評価します。
3. R言語によるシミュレーションコードと結果
以下に、上記のシナリオに基づいたシミュレーションをR言語で実行するコードを示します。
1. シナリオに基づいたデータ生成
# 必要なパッケージを読み込む
library(ggplot2)
library(dplyr)
library(tidyr) # pivot_longer用
# シミュレーションの再現性を確保するために乱数シードを固定
seed <- 20250728
set.seed(seed)
# --- 1. シナリオに基づいたデータ生成 ---
n_healthy <- 150
n_sick <- 150
# 健康者群とがん患者群のマーカー数値を生成
data <- data.frame(
true_status = factor(
c(rep("健康", n_healthy), rep("がん", n_sick)),
levels = c("健康", "がん")
),
marker_value = c(
rnorm(n_healthy, mean = 50, sd = 10),
rnorm(n_sick, mean = 70, sd = 15)
)
)
cat(sprintf("生成されたデータ数: %d件 (健康者: %d件, がん患者: %d件)\n\n", nrow(data), n_healthy, n_sick))生成されたデータ数: 300件 (健康者: 150件, がん患者: 150件)2. 生成データの分布を可視化
- 2つのグループのマーカー数値の分布をヒストグラムで確認します。
- 分布の重なり具合が、分類の難しさを示しています。
# --- 2. 生成したデータの分布を可視化 ---
# ヒストグラムのプロット
dist_plot <- ggplot(data, aes(x = marker_value, fill = true_status)) +
geom_histogram(alpha = 0.7, position = "identity", bins = 30) +
scale_fill_manual(values = c("健康" = "dodgerblue", "がん" = "tomato")) +
labs(
title = "マーカー数値の分布(健康者 vs がん患者)",
x = "マーカー数値",
y = "人数",
fill = "実際の状態"
) +
theme_minimal()
print(dist_plot)3. ROC曲線の計算
しきい値を変化させながら、各点での真陽性率(TPR)と偽陽性率(FPR)を計算します。
# --- 3. ROC曲線の計算 ---
# しきい値の候補を決定(観測された全マーカー数値と-Inf, Inf)
thresholds <- sort(unique(c(-Inf, data$marker_value, Inf)))
# 各しきい値でTPRとFPRを計算
roc_data <- purrr::map_dfr(thresholds, function(th) {
# しきい値に基づいて予測
predicted_status <- ifelse(data$marker_value >= th, "がん", "健康")
# TP, FP, TN, FN を計算
TP <- sum(predicted_status == "がん" & data$true_status == "がん")
FP <- sum(predicted_status == "がん" & data$true_status == "健康")
# TN <- sum(predicted_status == "健康" & data$true_status == "健康")
# FN <- sum(predicted_status == "健康" & data$true_status == "がん")
# TPR と FPR を計算
TPR <- TP / n_sick
FPR <- FP / n_healthy
data.frame(threshold = th, FPR = FPR, TPR = TPR)
})
# --- 4. AUC (Area Under the Curve) の計算 ---
# 台形則を用いてROC曲線の下の面積を計算
# FPRでソートされていることを確認
roc_data <- roc_data %>% arrange(FPR, TPR)
# xの差分 * yの平均
auc_value <- sum(diff(roc_data$FPR) * (roc_data$TPR[-1] + roc_data$TPR[-length(roc_data$TPR)]) / 2)
cat(sprintf("計算されたAUC (Area Under the Curve) の値: %.4f\n", auc_value))計算されたAUC (Area Under the Curve) の値: 0.8519AUCが1に近いほど、性能が良いことを示します。(0.5はランダム、1.0は完璧な分類)
4. ROC曲線のプロット
計算結果を基に、ROC曲線をプロットします。
# --- 5. ROC曲線のプロット ---
roc_plot <- ggplot(roc_data, aes(x = FPR, y = TPR)) +
geom_line(color = "blue", linewidth = 1.2) +
geom_abline(intercept = 0, slope = 1, linetype = "dashed", color = "red", linewidth = 0.8) +
annotate("text", x = 0.5, y = 0.4, label = "ランダム分類", color = "red", angle = 45) +
annotate("text", x = 0.3, y = 0.6, label = paste0("AUC = ", round(auc_value, 3)), size = 5) +
scale_x_continuous(limits = c(0, 1), breaks = seq(0, 1, 0.2)) +
scale_y_continuous(limits = c(0, 1), breaks = seq(0, 1, 0.2)) +
labs(
title = "がん早期発見マーカーのROC曲線",
subtitle = "マーカーの診断性能評価",
x = "偽陽性率 (FPR = 1 - 特異度)",
y = "真陽性率 (TPR / 感度)"
) +
coord_fixed() + # 縦横比を1:1に固定
theme_minimal()
print(roc_plot)4. シミュレーション結果の解説
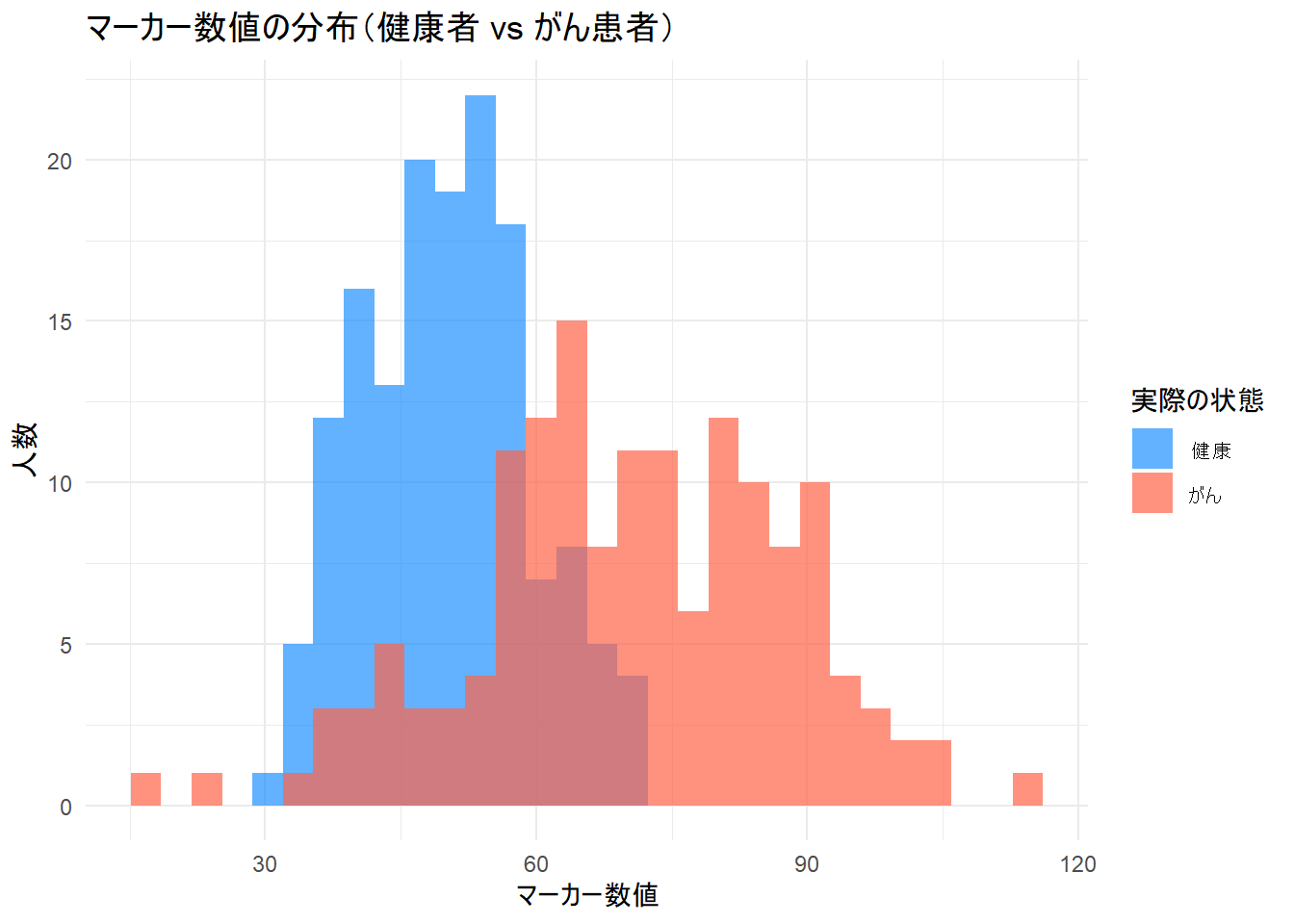
1. データ分布の可視化 Figure 1
まず、生成されたデータの分布をヒストグラムで確認します。青色が「健康者」、赤色が「がん患者」のマーカー数値の分布です。2つの分布は明確に分かれている部分もありますが、中央のマーカー数値50〜70あたりで大きく重なっています。この重なりがあるため、どこか一つのしきい値で完璧に2つのグループを分けることは不可能です。
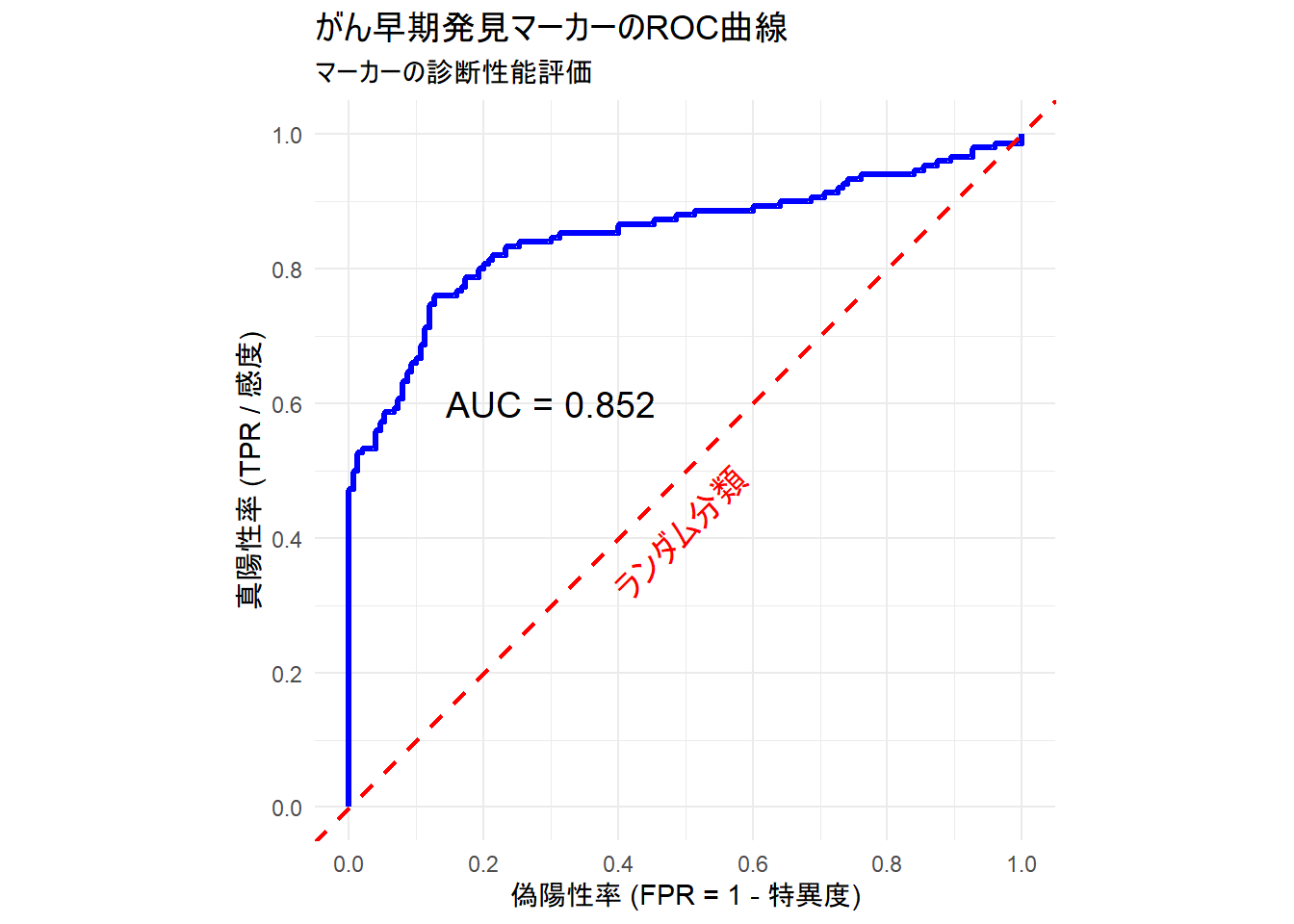
2. ROC曲線とAUC Figure 2
このROC曲線から以下のことが読み取れます。
- 性能評価: 青い実線で描かれたROC曲線は、赤い破線の「ランダム分類」よりも大きく左上に張り出しています。これは、このマーカーがランダム分類を上回る識別能を有することを示しています。
- AUC: AUCの値は約
0.852でした。これは一般的に「良い(Good)」分類器と見なされる水準であり、このマーカーがある程度の診断価値を持つことを定量的に示しています。 - しきい値のトレードオフ:
- もし、がんの見逃し(偽陰性)を絶対に避けたい場合、しきい値を低く設定します。これにより真陽性率(TPR)は1に近づきますが、偽陽性率(FPR)も高くなります(曲線が右上に移動)。つまり、多くの健康な人を「がんの疑いあり」と誤判定してしまい、不要な精密検査を増やすことになります。
- 逆に、健康な人を誤ってがんと診断すること(偽陽性)を避けたい場合、しきい値を高く設定します。これにより偽陽性率(FPR)は0に近づきますが、真陽性率(TPR)も低くなります(曲線が左下に移動)。つまり、実際のがん患者を見逃すリスクが高まります。
このように、ROC曲線は分類モデルの性能を視覚的に評価すると同時に、目的に応じて最適な「しきい値」を決定する際の重要な判断材料となります。
5. pROCパッケージを用いたROC曲線描画コード
1. ROCオブジェクトの計算
# 必要なパッケージを読み込む
library(pROC)
# --- 1. pROCパッケージでROCオブジェクトを計算 ---
# roc()関数に「実際の状態(response)」と「予測スコア(predictor)」を渡す
# levels引数で「陰性」「陽性」の順を指定することが重要
roc_obj <- roc(
response = data$true_status,
predictor = data$marker_value,
levels = c("健康", "がん") # 陰性(コントロール), 陽性(ケース) の順
)
# 計算されたROCオブジェクトのサマリーを表示
# AUCの値などが含まれている
cat("pROCによる計算結果サマリー:")
print(roc_obj)pROCによる計算結果サマリー:
Call:
roc.default(response = data$true_status, predictor = data$marker_value, levels = c("健康", "がん"))
Data: data$marker_value in 150 controls (data$true_status 健康) < 150 cases (data$true_status がん).
Area under the curve: 0.85192. ROC曲線の描画
# --- 2. pROCのplot関数でROC曲線を描画 ---
# plot関数で描画
plot(roc_obj,
main = "がん早期発見マーカーのROC曲線 (pROCパッケージ使用)",
print.auc = TRUE, # プロット内にAUCの値を表示
auc.col = "darkblue", # AUCテキストの色
auc.x = 0.45, # AUCテキストのx座標
auc.y = 0.3, # AUCテキストのy座標
col = "darkgreen", # ROC曲線の色
lwd = 2.5, # 線の太さ
print.thres = "best", # 最適なしきい値をプロット上に表示
print.thres.best.method = "youden", # 最適の基準(Youden Index)
print.thres.col = "red", # しきい値の点の色
legacy.axes = TRUE
)3. 実行結果の解説
1. 計算結果サマリー
roc()関数を実行し、その結果を表示すると上記のようなサマリーが出力されます。
Area under the curve: 0.8519 と、スクラッチコードの結果と一致しています。
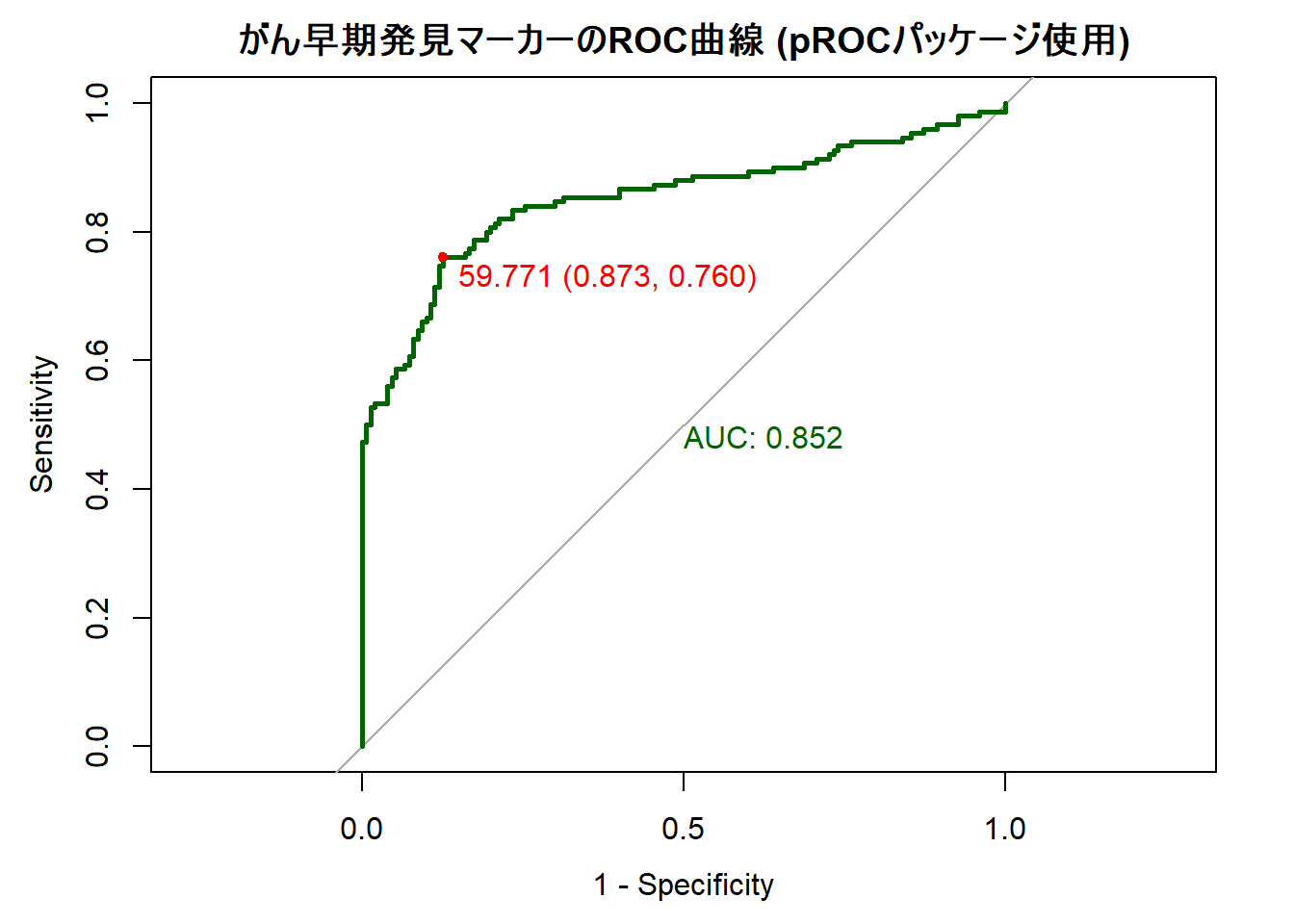
2. 描画されたROC曲線
plot()関数によって、Figure 3 のROC曲線が描画されます。
- 基本的な曲線: 緑色の実線でROC曲線が描かれています。
- AUCの表示:
print.auc = TRUEを指定したため、プロット内に「AUC: 0.852」のようにAUCの値が表示されます。 - 最適なしきい値:
print.thres = "best"を指定したことで、プロット上に赤い点で 最適なしきい値 が示されています。これは「Youden Index(感度 + 特異度 - 1)」が最大となる点で、感度と特異度のバランスが最も良いとされるポイントです。この点に対応する感度、特異度、しきい値の値も表示されます。このマーカーの場合、しきい値を約59.8に設定するのが最もバランスが良い、という一つの答えが得られます。
6. Youden Indexの算出
1. Youden Indexとは
Youden Index(J)は、ROC曲線上の点と、ランダム分類を示す対角線との垂直距離が最大になる点を探すための指標です。以下の式で計算されます。
\[
J = \text{感度} + \text{特異度} - 1
\]
ROC曲線の縦軸は感度(TPR)、横軸は偽陽性率(FPR)であり、特異度 = 1 - FPR という関係があります。これを代入すると、
\[
J = \text{TPR} + (1 - \text{FPR}) - 1 = \text{TPR} - \text{FPR}
\]
となり、結局 「真陽性率(TPR)と偽陽性率(FPR)の差が最大になる点」 を探せばよいことになります。
2. 最適しきい値(Youden Indexが最大となる最適点)の計算コード
以下に、Youden Indexが最大となる点を特定するコードを示します。
# roc_dataにYouden Index (TPR - FPR) の列を追加
roc_data_with_youden <- roc_data %>%
mutate(youden_index = TPR - FPR)
# Youden Indexが最大になる行を特定する
# slice_maxは最大値を持つ行を抽出する関数
best_point <- roc_data_with_youden %>%
dplyr::slice_max(youden_index, n = 1, with_ties = FALSE) # with_ties=FALSEで同率一位は最初のものに
# 結果の表示
cat(sprintf("最適なしきい値(Youden Indexを最大化する最適なしきい値): %.4f\n", best_point$threshold))
cat(sprintf(" - その時の真陽性率 (感度): %.4f (%.1f%%)\n", best_point$TPR, best_point$TPR * 100))
cat(sprintf(" - その時の偽陽性率: %.4f (%.1f%%)\n", best_point$FPR, best_point$FPR * 100))
cat(sprintf(" - その時の特異度 (1 - FPR): %.4f (%.1f%%)\n", 1 - best_point$FPR, (1 - best_point$FPR) * 100))
cat(sprintf(" - Youden Indexの最大値: %.4f\n", best_point$youden_index))最適なしきい値(Youden Indexを最大化する最適なしきい値): 59.8000
- その時の真陽性率 (感度): 0.7600 (76.0%)
- その時の偽陽性率: 0.1267 (12.7%)
- その時の特異度 (1 - FPR): 0.8733 (87.3%)
- Youden Indexの最大値: 0.6333- 感度と特異度のバランスが最も良いとされる「最適しきい値」が
59.800であることが計算できました。 - このしきい値を採用した場合、がん患者の76.0%を正しく「陽性」と判定でき(感度)、健康な人の87.3%を正しく「陰性」と判定できる(特異度)ことになります。
以上です。