RStan:一般化線形モデル(誤差構造=ガンマ分布,リンク関数=対数関数)

seed <- 20250702
set.seed(seed)

# データ生成
N <- 200 # ユーザー数

# 真のパラメータを設定
beta_0_true <- log(90) # オーガニック流入で訪問回数1回のユーザーの平均滞在時間(秒)の対数 (exp(4.5) ≈ 90秒)
beta_1_true <- -0.4 # 広告経由の効果 (滞在時間が exp(-0.4) ≈ 0.67倍になる)
beta_2_true <- 0.3 # 訪問回数(対数)の効果 (訪問回数が多いほど滞在時間が延びる)
phi_true <- 5 # ガンマ分布の形状パラメータ(shape)。値が大きいほど分散が小さくなる。

# 説明変数の生成
# X1: 広告経由ダミー (0: オーガニック, 1: 広告)
ad_flg <- rbinom(N, 1, 0.4)

# X2: サイト訪問回数 (ポアソン分布で生成し、1回以上とする)
visits <- rpois(N, lambda = 5) + 1

# 線形予測子 eta = log(mu)
eta <- beta_0_true + beta_1_true * ad_flg + beta_2_true * log(visits)

# 平均 mu
mu <- exp(eta)

# 応答変数Y (滞在時間) をガンマ分布から生成
# rate = shape / mean = phi / mu
stay_time <- rgamma(n = N, shape = phi_true, rate = phi_true / mu)

# データフレームにまとめる
sim_data <- data.frame(
  stay_time = stay_time,
  ad_flg = ad_flg,
  visits = visits,
  log_visits = log(visits)
)

# 生成したデータの分布を確認
library(ggplot2)
ggplot(sim_data, aes(x = stay_time)) +
  geom_histogram(bins = 30, fill = "skyblue", color = "black") +
  labs(
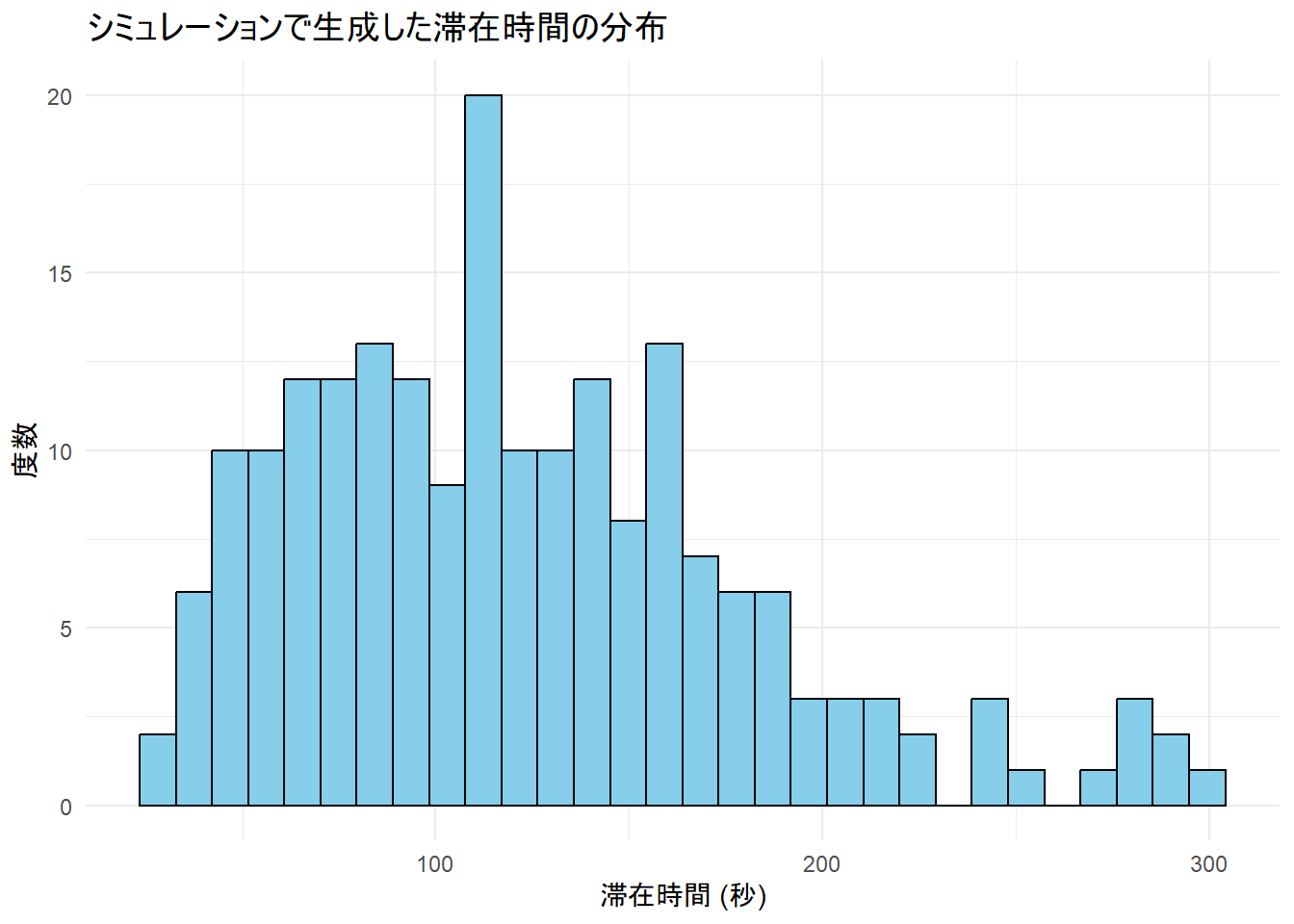
    title = "シミュレーションで生成した滞在時間の分布",
    x = "滞在時間 (秒)", y = "度数"
  ) +
  theme_minimal()

# stanfit オブジェクトの読み込み
setwd(stan_output)
fit <- readRDS("stan_fit.rds")

# 結果の要約
cat("--- 結果の要約 ---\n")
summary(fit,
  pars = c("beta", "phi"),
  probs = c(0.025, 0.5, 0.975)
)$summary
# 真の値: beta0=4.5, beta1=-0.4, beta2=0.3, phi=5

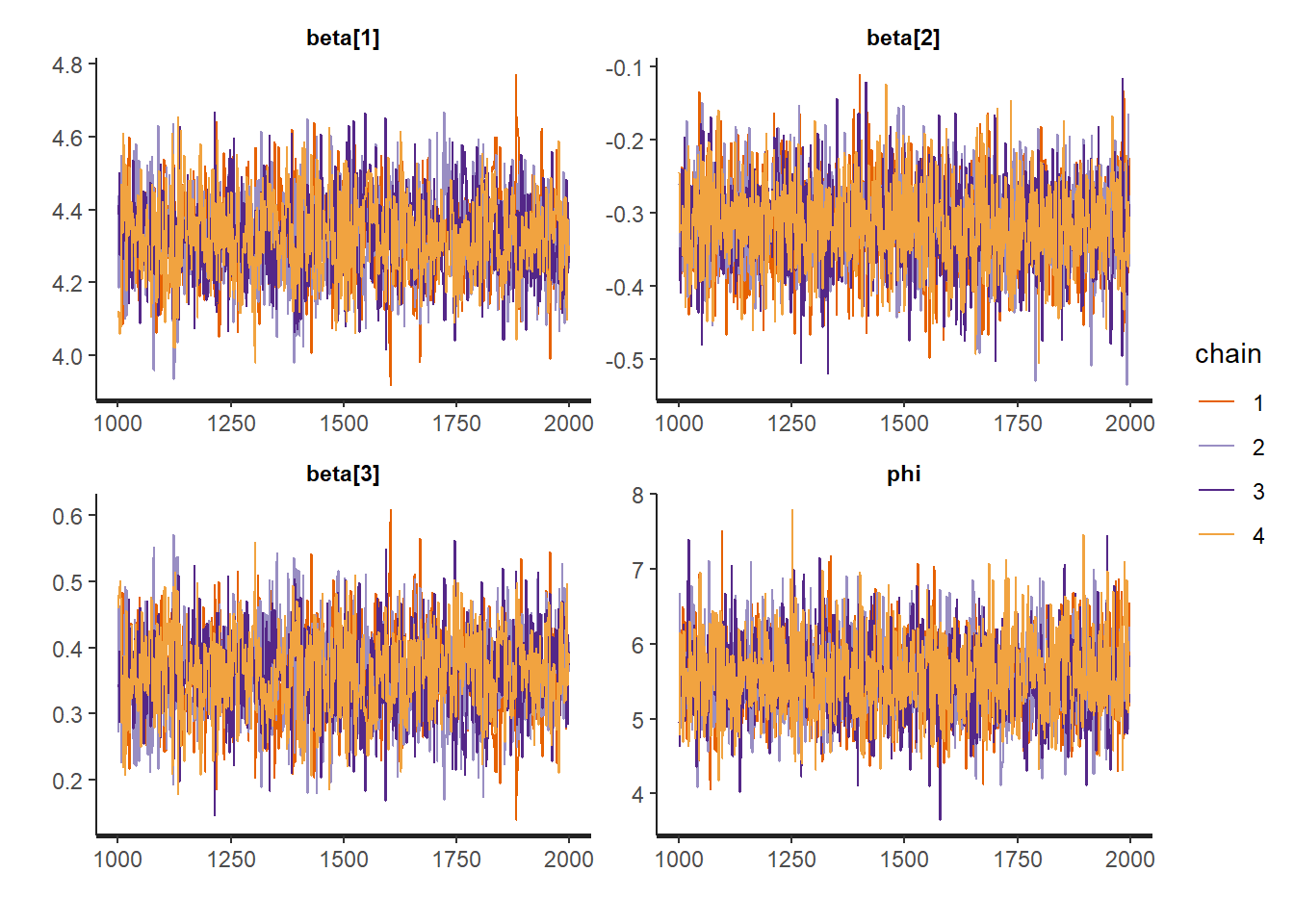
# トレースプロットで収束を確認
stan_trace(fit, pars = c("beta", "phi"))

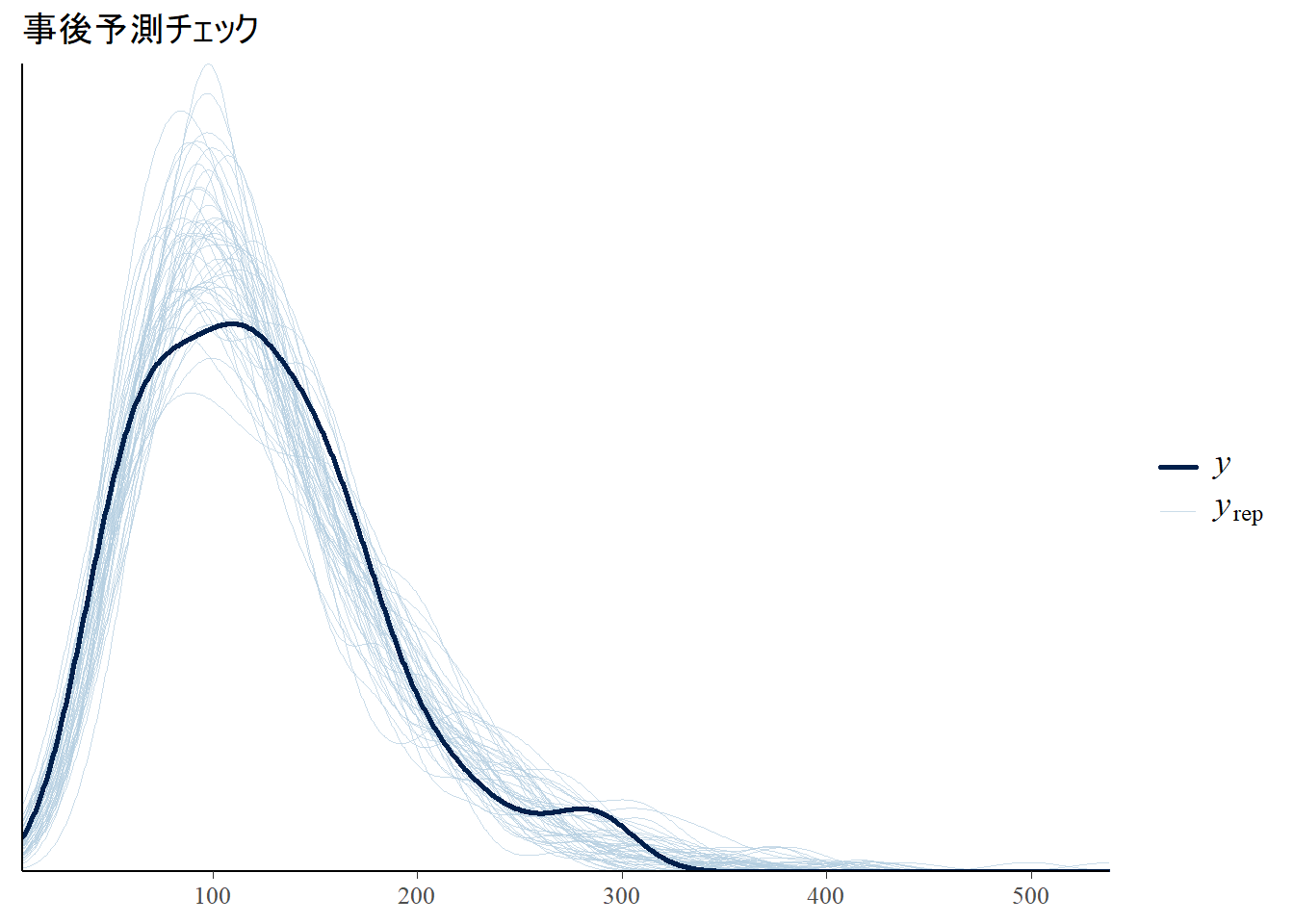
# 事後予測チェック
bayesplot::ppc_dens_overlay(y = sim_data$stay_time, yrep = as.matrix(fit, pars = "y_rep")[1:50, ]) +
  labs(title = "事後予測チェック")

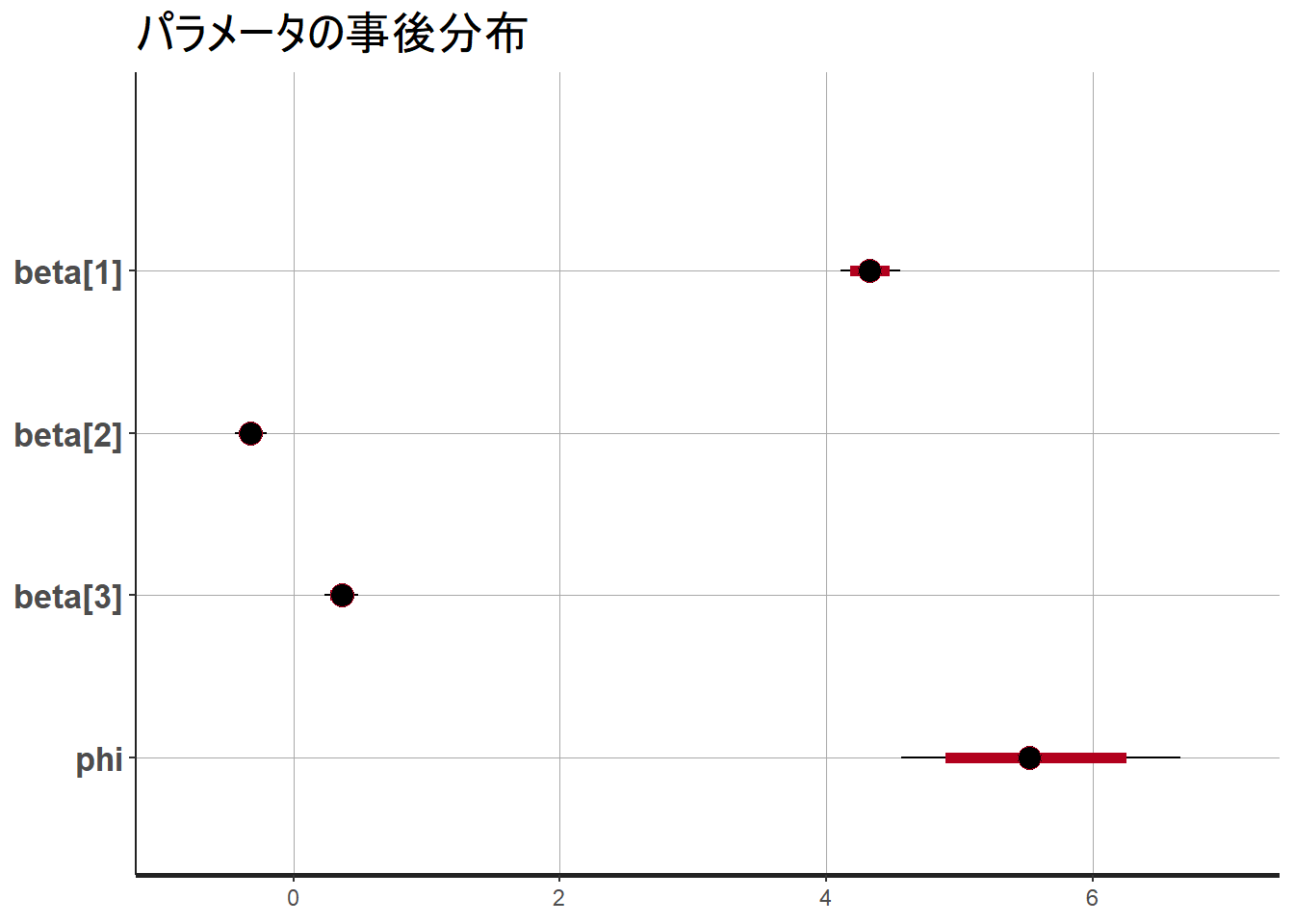
# パラメータの事後分布
stan_plot(fit, pars = c("beta", "phi")) +
  labs(title = "パラメータの事後分布")

# MCMCサンプルからbetaの事後分布をマトリックスとして抽出
beta_samples <- as.matrix(fit, pars = "beta")

# 予測用のデータグリッドを作成
pred_grid <- expand.grid(
  ad_flg = c(0, 1),
  log_visits = seq(min(sim_data$log_visits), max(sim_data$log_visits), length.out = 50)
)
pred_grid$visits <- exp(pred_grid$log_visits)

# 予測値を計算するための計画行列を作成
X_pred <- model.matrix(~ ad_flg + log_visits, data = pred_grid)

# X_pred (100x3) と beta_samplesの転置 (3x4000) の行列積を計算
# これにより、各MCMCサンプルにおける各予測点の平均値(mu)が得られる
mu_pred_samples <- exp(X_pred %*% t(beta_samples))

# 予測値の要約統計量（中央値、95%信用区間）を計算
pred_summary <- data.frame(
  pred_grid,
  median = apply(mu_pred_samples, 1, median),
  lower = apply(mu_pred_samples, 1, quantile, probs = 0.025),
  upper = apply(mu_pred_samples, 1, quantile, probs = 0.975)
)

# 凡例用のラベルを作成
pred_summary$ad_label <- factor(pred_summary$ad_flg, levels = c(0, 1), labels = c("オーガニック", "広告経由"))
sim_data$ad_label <- factor(sim_data$ad_flg, levels = c(0, 1), labels = c("オーガニック", "広告経由"))

# グラフを作成
ggplot(pred_summary, aes(x = visits, y = median, color = ad_label, fill = ad_label)) +
  geom_line(linewidth = 1) +
  geom_ribbon(aes(ymin = lower, ymax = upper), alpha = 0.2, linetype = "dotted") +
  geom_point(data = sim_data, aes(x = visits, y = stay_time, color = ad_label), alpha = 0.6) +
  scale_x_log10() +
  labs(
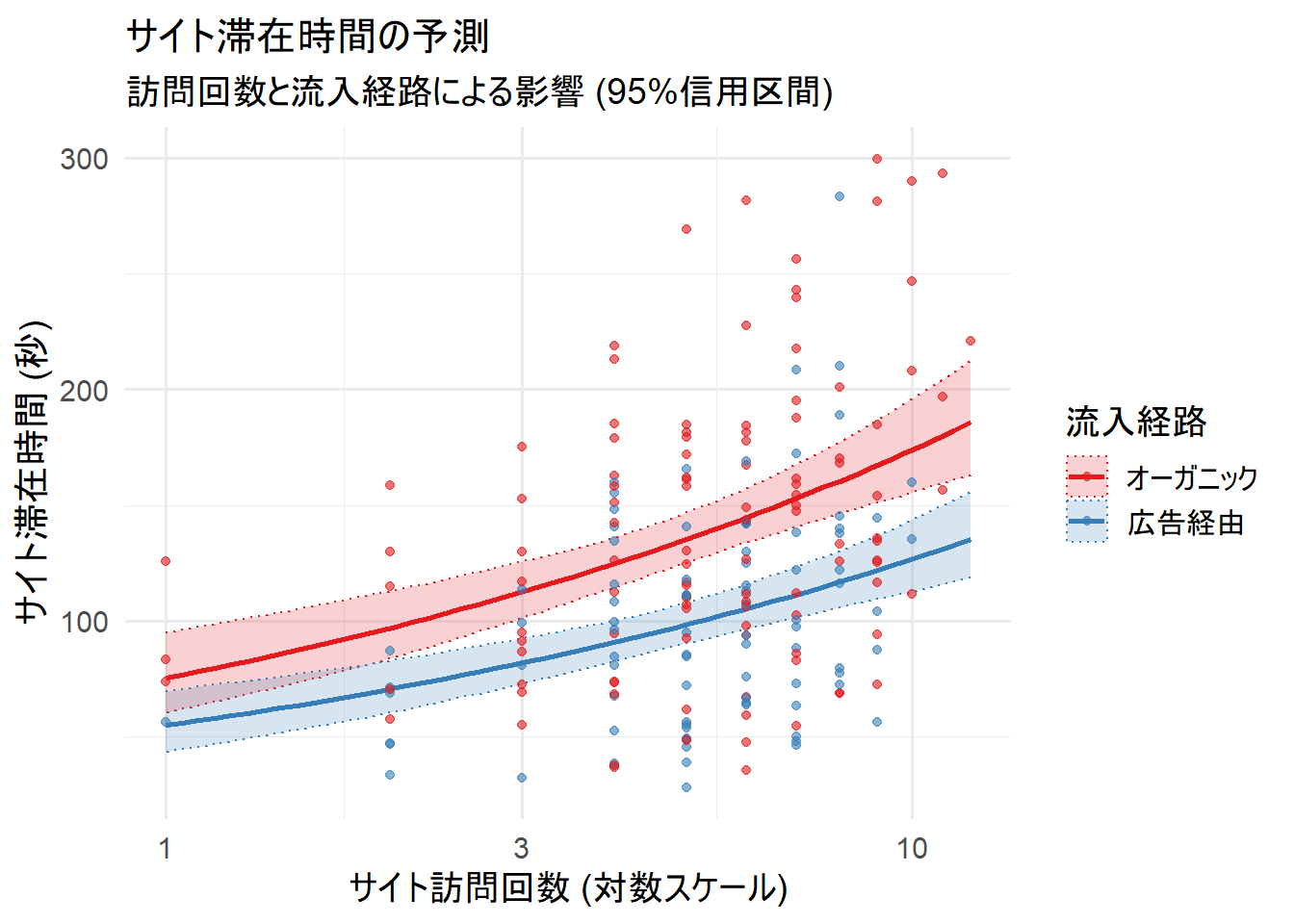
    title = "サイト滞在時間の予測",
    subtitle = "訪問回数と流入経路による影響 (95%信用区間)",
    x = "サイト訪問回数 (対数スケール)",
    y = "サイト滞在時間 (秒)",
    color = "流入経路",
    fill = "流入経路"
  ) +
  theme_minimal(base_size = 14) +
  scale_color_brewer(palette = "Set1") +
  scale_fill_brewer(palette = "Set1")