Rで 相関係数:スピアマンの順位相関係数 を試みます。
本ポストはこちらの続きです。

1. スピアマンの順位相関係数とは
スピアマンの順位相関係数(Spearman’s rank correlation coefficient)は、2つの変数の関係性の強さを測る指標の一つですが、ピアソンの積率相関係数とは異なり、実際の値ではなく順位(ランク)に基づいて計算されます。記号としては \(\rho_s\) や \(r_s\) が用いられます。
この相関係数には、主に2つの大きな特徴があります。
- 非線形な単調関係も捉えられる: 2つの変数の関係が、一貫して増加(または減少)する「単調関係」ではあるものの、直線的ではない場合(例:最初は急激に増え、後から伸び悩むなど)でも、その関連の強さを評価できます。
- 外れ値に強い(頑健である): データの値そのものではなく、順位を用いるため、極端に大きな値や小さな値(外れ値)が存在しても、その影響を受けにくいという利点があります。
計算方法
スピアマンの順位相関係数を計算するプロセスは以下の通りです。
- 2つの変数 \(X, Y\) の各データについて、それぞれ順位をつけます。小さい値から1位、2位、…と順位をつけます。(値が同じ場合は、それらの順位の平均値を割り当てます。例えば、3位と4位が同じ値なら、両方に3.5位を与えます。)
- 変数 \(X\) の順位を \(R(X)\)、変数 \(Y\) の順位を \(R(Y)\) とします。
- この2つの順位データ \(R(X)\) と \(R(Y)\) を用いて、ピアソンの積率相関係数を計算します。これがスピアマンの順位相関係数となります。
\[
\rho_s = \rho_{R(X), R(Y)} = \dfrac{\mathrm{cov}(R(X), R(Y))}{\sigma_{R(X)}\sigma_{R(Y)}}
\]
ここで、\(\mathrm{cov}\) は共分散、\(\sigma\) は標準偏差を表します。
同順位がない場合の計算式
もしデータに同順位(タイ)が一つも存在しない場合は、より簡単な以下の計算式を用いることができます。
\[
\rho_s = 1 - \dfrac{6 \displaystyle\sum_{i=1}^{n} d_i^2}{n\left(n^2 - 1\right)}
\]
ここで、
- \(d_i\) は、各データペアの順位の差 (\(R(X_i) - R(Y_i)\)) です。
- \(n\) は、データペアの数です。
この式からわかるように、順位の差 \(d_i\) が小さいほど、合計値 \(\sum d_i^2\) は小さくなり、\(\rho_s\) は1に近づきます。これは、2つの変数の順位がよく似ている(強い正の相関)ことを意味します。
2. シミュレーションに適したシナリオ
スピアマンの順位相関係数が特に有効な「非線形な単調関係」をテーマに、以下のシナリオを設定します。
シナリオ:学習時間とテストの点数 ~伸び悩みの壁~
ある資格試験の予備校が、生徒たちの「総学習時間」と「模擬試験の点数」の関係を分析しています。
- 変数X:総学習時間
- 変数Y:模擬試験の点数
一般的に、学習時間が増えれば点数も上がると期待されます。しかし、その関係は必ずしも直線的ではありません。
- 初期段階: 学習を始めたばかりの頃は、勉強すればするだけ知識が身につき、点数は急激に伸びます。(例:0時間→50時間)
- 中級段階: ある程度の実力がつくと、同じ時間勉強しても、点数の伸びは緩やかになります。(例:100時間→150時間)
- 上級段階: 高得点域になると、1点を上げるために膨大な学習時間が必要になり、点数はほとんど頭打ち(飽和)状態になります。(例:200時間→250時間)
このような「効果が逓減(ていげん)していく関係」は、直線ではありませんが、「学習時間が増えれば点数が下がることはない」という単調増加の関係です。
このデータをピアソンの積率相関係数で分析すると、直線からのズレが大きいため、関係性を過小評価してしまう可能性があります。一方で、スピアマンの順位相関係数を使えば、「学習時間の順位が高い生徒は、点数の順位も高い」という単調な関係性を正しく捉えることができるはずです。
3. R言語によるシミュレーション
上記のシナリオに沿って、R言語でシミュレーションを行い、ピアソンの相関係数とスピアマンの順位相関係数の違いを視覚的に確認します。
準備
必要なライブラリを読み込みます。
# ライブラリの読み込み
library(ggplot2)
library(dplyr)シミュレーションコード
# 再現性のために乱数のシードを固定
seed <- 20250823
set.seed(seed)
# データ数(生徒の数)
n <- 150
# 1. データ生成
# 変数X: 総学習時間
study_time <- runif(n, 0, 1000)
# 変数Y: 模擬試験の点数
base_score <- 20
# log1p(x) = log(1+x)
score_gain <- 10 * log1p(study_time)
noise <- rnorm(n, mean = 0, sd = 2.5)
test_score <- base_score + score_gain + noise
# データをデータフレームにまとめる
sim_data <- data.frame(
study_time = study_time,
test_score = test_score
)
# 2. 相関係数の計算と比較
cat("--- 相関係数の比較 ---\n")
# ピアソンの積率相関係数
pearson_cor <- cor(sim_data$study_time, sim_data$test_score, method = "pearson")
cat(paste0("ピアソンの積率相関係数: ", round(pearson_cor, 3), "\n"))
cat("→ 直線的な関係を仮定するため、非線形な関係をやや過小評価しています。\n\n")
# スピアマンの順位相関係数
spearman_cor <- cor(sim_data$study_time, sim_data$test_score, method = "spearman")
cat(paste0("スピアマンの順位相関係数: ", round(spearman_cor, 3), "\n"))
cat("→ 順位に基づいているため、単調増加の関係をより強く捉え、高い値を示しています。\n\n")
# 3. 可視化
# 3-1. 元データの散布図
g1 <- ggplot(sim_data, aes(x = study_time, y = test_score)) +
geom_point(alpha = 0.7, color = "dodgerblue") +
geom_smooth(method = "lm", aes(color = "ピアソン(直線)"), se = FALSE, linewidth = 1.2) +
geom_smooth(method = "loess", aes(color = "データ全体の傾向"), se = FALSE, linewidth = 1.2) +
scale_color_manual(name = "近似線", values = c("ピアソン(直線)" = "red", "データ全体の傾向" = "black")) +
labs(
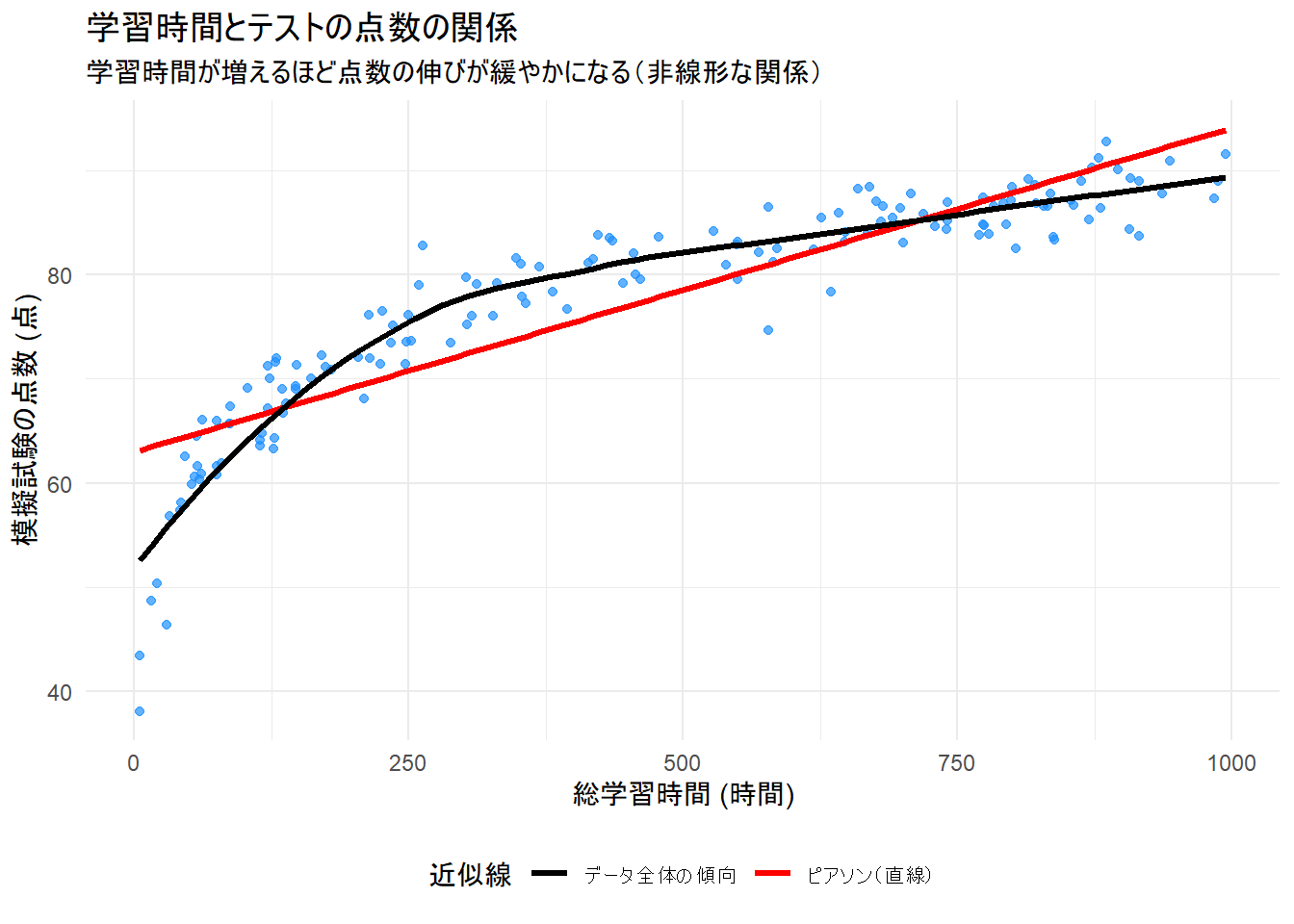
title = "学習時間とテストの点数の関係",
subtitle = "学習時間が増えるほど点数の伸びが緩やかになる(非線形な関係)",
x = "総学習時間 (時間)",
y = "模擬試験の点数 (点)"
) +
theme_minimal() +
theme(legend.position = "bottom")
print(g1)
# 3-2. 順位データの散布図
# スピアマンの相関係数は、データを順位に変換してから相関を見ています。
# データに順位の列を追加
rank_data <- sim_data %>%
mutate(
rank_time = rank(study_time),
rank_score = rank(test_score)
)
g2 <- ggplot(rank_data, aes(x = rank_time, y = rank_score)) +
geom_point(alpha = 0.7, color = "forestgreen") +
geom_smooth(method = "lm", se = FALSE, color = "orange", linewidth = 1.2) +
labs(
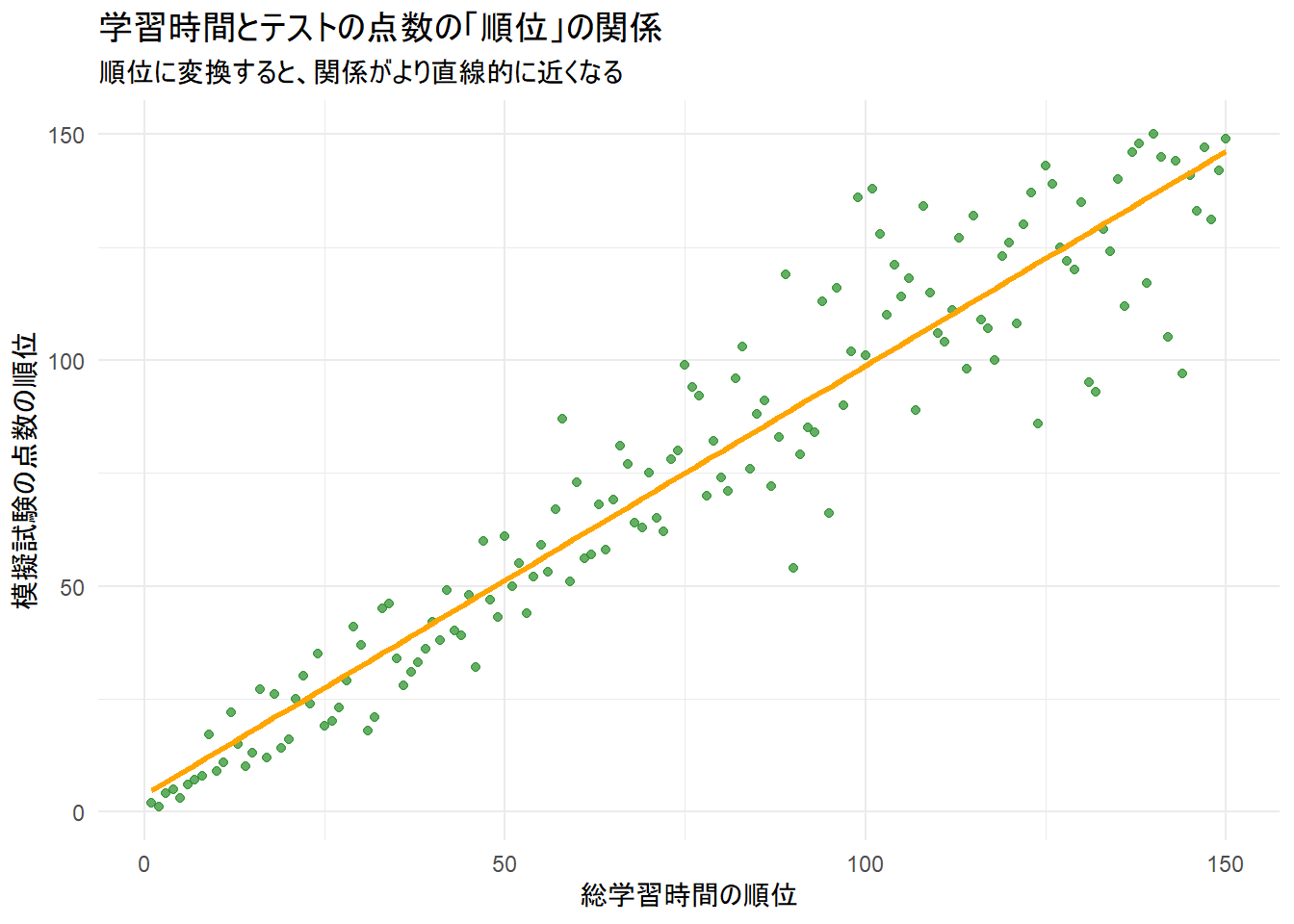
title = "学習時間とテストの点数の「順位」の関係",
subtitle = "順位に変換すると、関係がより直線的に近くなる",
x = "総学習時間の順位",
y = "模擬試験の点数の順位"
) +
theme_minimal()
print(g2)--- 相関係数の比較 ---
ピアソンの積率相関係数: 0.883
→ 直線的な関係を仮定するため、非線形な関係をやや過小評価しています。
スピアマンの順位相関係数: 0.95
→ 順位に基づいているため、単調増加の関係をより強く捉え、高い値を示しています。シミュレーション結果の解説
- 相関係数の比較:
- ピアソンの積率相関係数は
0.883と算出されました。これは十分に高い値ですが、データの非線形性により、関係の強さを完全には捉えきれていません。 - スピアマンの順位相関係数は
0.95と算出されました。ピアソンよりも1に近い値です。これは、「学習時間の順位が高い生徒は、テストの点数の順位も高い」というシナリオ通りの単調な関係が、より正しく評価されていることを示唆しています。
- ピアソンの積率相関係数は
- 元データの可視化: Figure 1 は、横軸に学習時間、縦軸にテストの点数を取ったものです。
- 点が右に行くほど、上に行く傾向はありますが、その伸び方は徐々に緩やかになっています。
- 赤い直線(ピアソンが評価する関係)は、データ全体の傾向をうまく捉えきれておらず、特に学習時間が短い領域でデータから乖離しています。
- 黒い曲線はデータの傾向を捉えており、このデータが非線形であることが視覚的にわかります。
- 順位データの可視化: Figure 2 は、両方の変数を順位に変換した後の散布図です。
- Figure 1 に見られたカーブが解消され、点が直線に近い形で分布しているのがわかります。
- 順位の一致度を測る指標ですので、計算過程において残差の均一性を仮定していません。
以上です。