Rで 確率分布:パレート分布 を試みます。
本ポストはこちらの続きです。

1. パレート分布とは
パレート分布(Pareto Distribution)は、イタリアの経済学者ヴィルフレド・パレートにちなんで名付けられた確率分布です。この分布は、「全体の数値の大部分は、全体を構成するうちの一部の要素が生み出している」という現象をモデル化するために用いられます。これはしばしば「パレートの法則」や「80-20の法則」(例:売上の8割は2割の顧客が生み出す)として知られています。
数学的には、パレート分布はべき乗則(Power Law)に従う分布の一種であり、その最大の特徴は、非常に長く重い裾(ヘビーテール)を持つことです。これにより、所得や富の分布など、ごく少数の要素が極端に大きな値をとるような現象を記述するのに適しています。
確率密度関数 (Probability Density Function, PDF)
パレート分布に従う確率変数 \(X\) の確率密度関数 \(f(x)\) は、2つのパラメータを用いて以下のように定義されます。
\[f\left(x | x_m, \alpha\right) = \dfrac{\alpha x_m^\alpha}{x^{\alpha+1}} \quad (x \ge x_m)\]
この分布は、2つのパラメータによってその形状が決定されます。
- \(x_m\): 尺度パラメータ (scale parameter)
- 分布が取りうる最小値を決定する正のパラメータです。分布の「始まり」の位置を示します。
- \(\alpha\) (アルファ): 形状パラメータ (shape parameter)
- 分布の裾の重さ(減衰の速さ)を決定する正のパラメータです。しばしばパレート指数と呼ばれます。
- \(\alpha\) が小さいほど、裾はより重くなり(減少が緩やかになり)、極端な値が出現する確率が高くなります。
- \(\alpha\) が大きいほど、裾はより軽くなり(減少が急になり)、値はより均等に近づきます。
主な特徴
- 定義域: 確率変数は、最小値 \(x_m\) 以上の値 (\(x \ge x_m\)) をとります。
- 形状: \(x_m\)で最大値をとり、その後べき乗的に単調減少する、右に長く重い裾を持つ形状をしています。
- 平均・分散の存在条件: パレート分布のもう一つの重要な特徴は、形状パラメータ \(\alpha\) の値によって平均や分散が存在しない場合があることです。
- 平均 (Mean): \(E[X] = \dfrac{\alpha x_m}{\alpha-1}\) (ただし、\(\alpha > 1\) の場合のみ存在)
- 分散 (Variance): \(V[X] = \left(\dfrac{x_m}{\alpha-1}\right)^2 \dfrac{\alpha}{\alpha-2}\) (ただし、\(\alpha > 2\) の場合のみ存在)
- スケールフリー性: パレート分布はスケールフリー(スケール不変性)と呼ばれる性質を持ちます。これは、分布をどのスケールで見ても、その全体的な形状の統計的性質が変わらないことを意味し、自己相似性を持つフラクタル構造などと関連が深いです。
2. パレート分布の応用例
「勝者総取り(winner-take-all)」のような現象が見られる多くの分野で応用されます。
- 社会科学・経済学
- 所得・富の分布: 上位数パーセントの富裕層が、社会全体の富の大半を所有する状況をモデル化します。
- 都市の人口規模: 少数の巨大都市に人口が集中し、多くの小さな市町村が存在する分布(ジップの法則)。
- ウェブサイトの被リンク数: 一部の人気サイトがほとんどのリンクを獲得する分布。
- 自然科学
- 地震の規模: マグニチュードの小さい地震は頻繁に起こるが、巨大地震は非常に稀であるという分布。
- 隕石のサイズ: 小さな隕石は無数に存在するが、巨大なものは滅多にないという分布。
- 保険数理
- 自然災害などによる保険金の支払い額のモデル化。ほとんどは小額の支払いだが、ごく稀に壊滅的な額の支払いが発生する状況を記述します。
3. R言語によるシミュレーション
ここでは、最小値 \(x_m\) を固定し、形状パラメータ \(\alpha\) を変更した3つのパレート分布を1枚のチャートに描画します。これにより、\(\alpha\) が分布の裾の重さに与える影響を視覚的に理解します。
- ケース1:
xm=1, α=0.5(\(\alpha \le 1\)。平均・分散が存在しない、非常に重い裾) - ケース2:
xm=1, α=1.5(\(1 < \alpha \le 2\)。平均は存在するが、分散は存在しない) - ケース3:
xm=1, α=2.5(\(\alpha > 2\)。平均・分散ともに存在する)
Rコード
# 必要なライブラリを読み込みます
library(ggplot2)
library(dplyr)
library(tidyr)
# パレート分布の確率密度関数(PDF)を定義
d_pareto <- function(x, xm, alpha) {
# xがxmより小さい場合は密度0、そうでなければ公式を適用
ifelse(x < xm, 0, (alpha * xm^alpha) / (x^(alpha + 1)))
}
# 1. 描画範囲となるx軸の値を生成
x_vals <- seq(0.1, 10, length.out = 1000)
# 2. 異なるパラメータを持つパレート分布の確率密度を計算
df <- tibble(
x = x_vals
) %>%
mutate(
`α=0.5 (平均なし)` = d_pareto(x, xm = 1, alpha = 0.5),
`α=1.5 (分散なし)` = d_pareto(x, xm = 1, alpha = 1.5),
`α=2.5 (分散あり)` = d_pareto(x, xm = 1, alpha = 2.5)
)
# 3. ggplotで描画しやすいように、データを「ロングフォーマット」に変換
df_long <- df %>%
pivot_longer(
cols = -x,
names_to = "parameters",
values_to = "density"
) %>%
# 凡例の順序を調整
mutate(parameters = factor(parameters, levels = c(
"α=0.5 (平均なし)",
"α=1.5 (分散なし)",
"α=2.5 (分散あり)"
)))
# 4. 各分布に割り当てる色を定義
manual_colors <- c(
`α=0.5 (平均なし)` = "blue",
`α=1.5 (分散なし)` = "red",
`α=2.5 (分散あり)` = "darkgreen"
)
# 5. ggplotを使用してチャートを描画
p <- ggplot(df_long, aes(x = x, y = density, color = parameters)) +
geom_line(linewidth = 1.2) +
scale_color_manual(values = manual_colors) +
labs(
title = "形状パラメータ(α)によるパレート分布の変化 (xm=1で固定)",
subtitle = "αが小さいほど裾が重く(減少が遅く)、極端な値が出やすい",
x = "xの値",
y = "確率密度",
color = "形状パラメータ (α)"
) +
coord_cartesian(xlim = c(0, 10), ylim = c(0, 2.6)) +
theme_minimal(base_size = 14) +
theme(
legend.position = "top",
plot.title = element_text(face = "bold"),
plot.subtitle = element_text(color = "gray40")
)
# チャートの表示
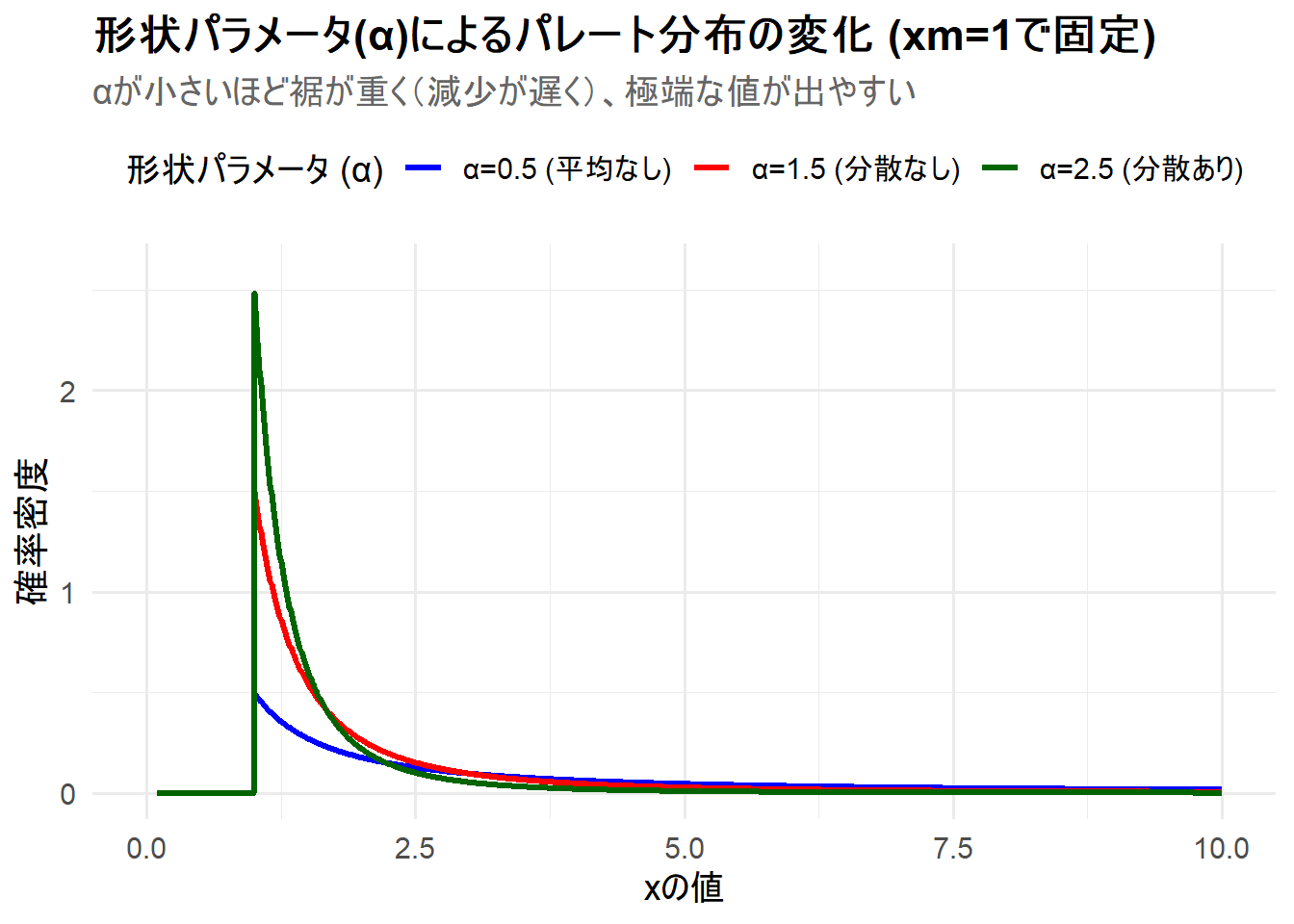
print(p)Figure 1 の解説
上記のRコードを実行すると、3つのパレート分布が描画されたチャート Figure 1 が生成されます。
-
α=0.5(青線): 形状パラメータが最も小さく、裾が最も重いケースです。\(x=1\)以降の確率密度の減少が緩やかで、他の分布よりも高い値を保っています(Figure 2)。これは、非常に大きな値が出現する確率が相対的に高いことを示しています。 -
α=1.5(赤線): \(\alpha\)が大きくなったことで、確率密度の減少が青線より急になっています。 -
α=2.5(緑線): 形状パラメータが最も大きく、確率密度の減少が最も急峻です。\(x=1\)の近くに確率が集中し、裾は他のケースより軽くなっています。
このシミュレーションから、形状パラメータ \(\alpha\) がパレート分布の「裾の重さ」をコントロールする上で決定的な役割を果たすことがわかります。
パレート分布のPDFは \(f(x) \propto x^{-(\alpha+1)}\) という形をしていますので \(x\) が分母にあるため、指数部分の \(\alpha+1\) が大きいほど、減少は速くなります。
- \(\alpha\) が小さい → 指数 \(\alpha+1\) が小さい → 減少が遅い → 裾が重い → 格差が大きい
- \(\alpha\) が大きい → 指数 \(\alpha+1\) が大きい → 減少が速い → 裾が軽い → 格差が小さい
つまり、\(\alpha\) が小さいほど、富の分布のように、ごく一部が全体の大半を占めるような、より極端な不均衡が生じやすくなります。
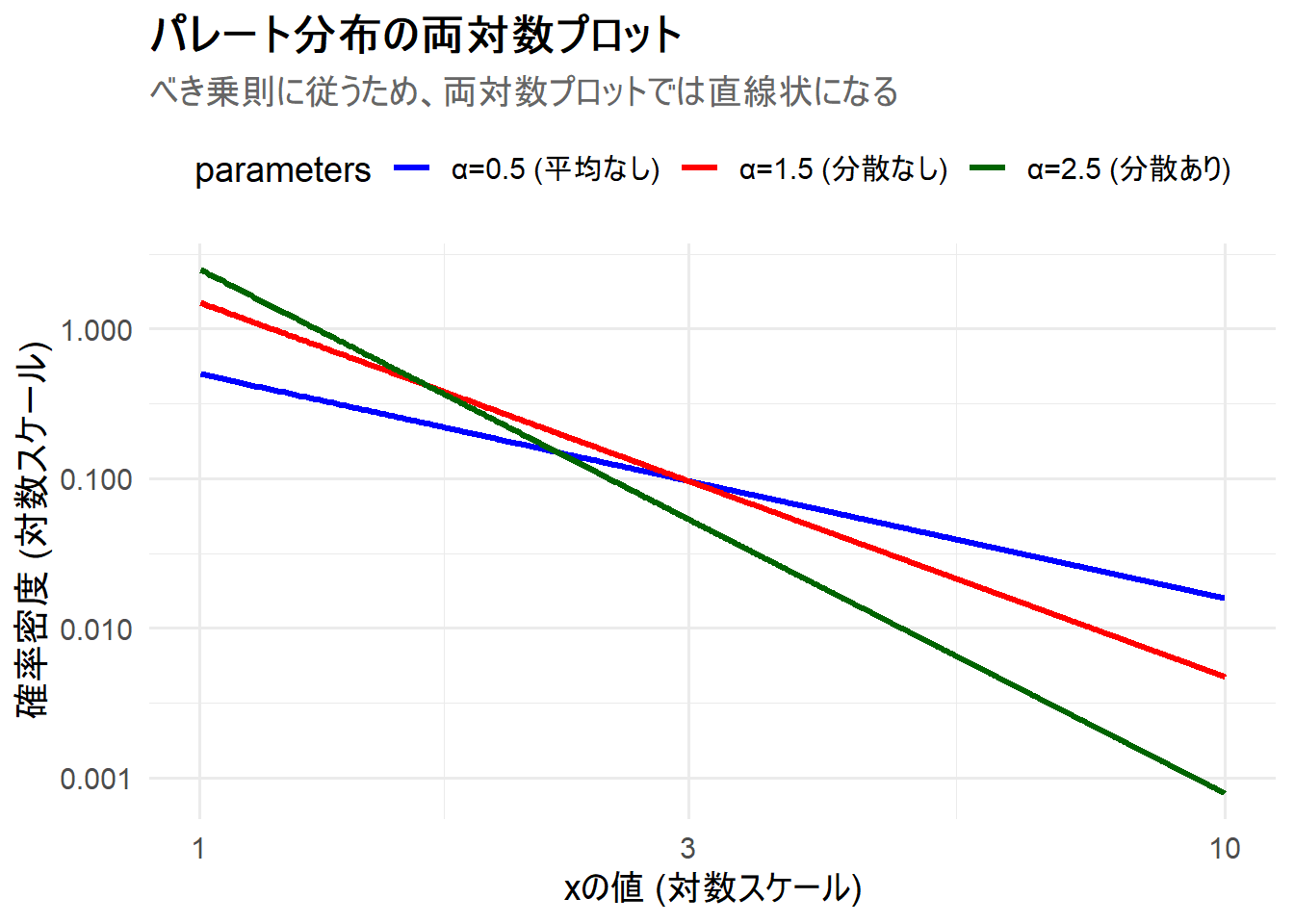
補足:べき乗則の可視化(両対数プロット)
パレート分布がべき乗則に従うという特徴は、x軸とy軸の両方を対数スケールにしてプロットするとより明確になります。この両対数プロットでは、パレート分布はほぼ直線として現れます。
# 両対数プロットを作成
p_loglog <- ggplot(filter(df_long, density > 0), aes(x = x, y = density, color = parameters)) +
geom_line(linewidth = 1.2) +
scale_color_manual(values = manual_colors) +
# 対数スケールを適用
scale_x_log10() +
scale_y_log10() +
labs(
title = "パレート分布の両対数プロット",
subtitle = "べき乗則に従うため、両対数プロットでは直線状になる",
x = "xの値 (対数スケール)",
y = "確率密度 (対数スケール)"
) +
theme_minimal(base_size = 14) +
theme(
legend.position = "top",
plot.title = element_text(face = "bold"),
plot.subtitle = element_text(color = "gray40")
)
# 両対数プロットを表示
print(p_loglog)以上です。