Rで確率分布:超幾何分布

Rで 確率分布:超幾何分布 を試みます。

本ポストはこちらの続きです。

const typesetMath = (el) => { if (window.MathJax) { // MathJax Typeset window.MathJax.typeset(); } else if (window.katex...

1. 超幾何分布とは

超幾何分布（Hypergeometric Distribution）は、「当たり」と「ハズレ」の2種類のものが入った母集団から、非復元抽出（一度引いたものは元に戻さない）で標本をいくつか引いたときに、その標本に含まれる「当たりの個数」が従う離散確率分布です。

二項分布が「復元抽出」（くじを引くたびに元に戻すため、当たりを引く確率は常に一定）の状況をモデル化するのに対し、超幾何分布は「非復元抽出」（くじを引くたびに当たりが減ったり、全体の数が減ったりするため、当たりを引く確率が変動する）の状況をモデル化する点が本質的な違いです。

確率質量関数 (PMF)

\(N\)個の要素からなる母集団に、\(K\)個の「当たり」が含まれているとします。この母集団から\(n\)個の標本を非復元抽出したとき、その中に\(k\)個の当たりが含まれる確率 \(P(X=k)\) は、以下の式で定義されます。

\[P\left(X=k | N, K, n\right) = \dfrac{\binom{K}{k} \binom{N-K}{n-k}}{\binom{N}{n}}\]

この式は、組み合わせの数の比で構成されています。

分母 \(\binom{N}{n}\): 全\(N\)個から\(n\)個を選ぶ、すべての可能な組み合わせの総数。
分子 \(\binom{K}{k} \binom{N-K}{n-k}\):
- \(\binom{K}{k}\): 全\(K\)個の当たりから\(k\)個を選ぶ組み合わせの数。
- \(\binom{N-K}{n-k}\): 全\(N-K\)個のハズレから、残りの\(n-k\)個を選ぶ組み合わせの数。
- これらの積が、条件を満たす組み合わせの数となります。

この分布は、3つのパラメータによってその形状が決定されます。

\(N\): 母集団の総数 (population size)
\(K\): 母集団に含まれる当たりの総数 (number of successes in population)
\(n\): 抽出する標本のサイズ (sample size)

主な特徴

定義域: 当たりの個数 \(k\) がとりうる値は、\(\max(0, n-(N-K)) \le k \le \min(n, K)\) の範囲の整数です。
形状: 二項分布と同様に、釣鐘型の分布になりますが、非復元抽出の影響で、二項分布よりも分散が小さく（ピークが鋭く）なる傾向があります。
代表値:
- 平均 (Mean): \(E[X] = n \dfrac{K}{N}\)
- 分散 (Variance): \(V[X] = n \dfrac{K}{N} \left(1-\dfrac{K}{N}\right) \dfrac{N-n}{N-1}\)
- 分散の式に現れる \(\dfrac{N-n}{N-1}\) は有限母集団修正（finite population correction）と呼ばれ、非復元抽出による分散の減少を表します。母集団の総数 \(N\) が標本サイズ \(n\) に比べて非常に大きい場合、この項は1に近づき、超幾何分布は二項分布で近似できます。

2. 超幾何分布の応用例

非復元抽出が本質となる場面で応用されます。

品質管理
- \(N\)個の製品ロットの中に\(K\)個の不良品が含まれていると仮定し、\(n\)個を抜き取り検査したときの、不良品の個数の確率分布。これにより、ロット全体の品質を推測し、合格・不合格を判定します。
遺伝学
- 特定の遺伝子を持つ個体が\(K\)匹いる、閉鎖された\(N\)匹の個体群から、\(n\)匹を捕獲したときの、その遺伝子を持つ個体の数。
カードゲーム
- 52枚のトランプの山札（\(N=52\)）から、最初に配られた5枚の手札（\(n=5\)）の中に、エース（\(K=4\)）が何枚含まれているか、といった確率の計算。
フィッシャーの正確確率検定
- 2×2の分割表における周辺度数を固定した条件下で、セルの度数が観測された値以上（あるいは以下）に偏る確率を計算するために、超幾何分布が直接利用されます。これは、サンプルサイズが小さい場合の独立性の検定で利用されます。

3. R言語によるシミュレーション

ここでは、パラメータを変更した3つの超幾何分布と、比較対象として対応する二項分布を1枚のチャートに描画します。これにより、非復元抽出の影響（有限母集団修正の効果）を視覚的に理解します。

ケース1: N=50, K=15, n=10 （標準的なケース）
ケース2: N=50, K=15, n=20 （抽出数を増やす）
ケース3: N=500, K=150, n=10 （母集団を大きくする → 二項分布に近づく）
比較対象: 二項分布 n=10, p=15/50 （ケース1に対応する復元抽出の場合）

Rコード

# 必要なライブラリを読み込みます
library(ggplot2)
library(dplyr)
library(tidyr)

# 1. 描画範囲となるx軸の値（当たりの個数）を生成
k_vals <- 0:20

# 2. 異なるパラメータを持つ超幾何分布と二項分布の確率質量を計算
# dhyper(x, m, n, k) -> x:当たりの個数, m:母集団の当たり数, n:母集団のハズレ数, k:抽出数
df <- tibble(
  k = k_vals
) %>%
  mutate(
    `N=50, K=15, n=10` = dhyper(k, m = 15, n = 50 - 15, k = 10),
    `N=50, K=15, n=20` = dhyper(k, m = 15, n = 50 - 15, k = 20),
    `N=500,K=150, n=10` = dhyper(k, m = 150, n = 500 - 150, k = 10),
    `二項分布(n=10,p=0.3)` = dbinom(k, size = 10, prob = 15 / 50)
  )

# 3. ggplotで描画しやすいように、データを「ロングフォーマット」に変換
df_long <- df %>%
  pivot_longer(
    cols = -k,
    names_to = "parameters",
    values_to = "probability"
  ) %>%
  filter(probability > 1e-9) %>%
  mutate(parameters = factor(parameters, levels = c(
    "N=50, K=15, n=10",
    "N=50, K=15, n=20",
    "N=500,K=150, n=10",
    "二項分布(n=10,p=0.3)"
  )))

# 4. 各分布に割り当てる色と線種を定義
manual_colors <- c(
  `N=50, K=15, n=10` = "blue",
  `N=50, K=15, n=20` = "red",
  `N=500,K=150, n=10` = "darkgreen",
  `二項分布(n=10,p=0.3)` = "black"
)
manual_linetypes <- c(
  `N=50, K=15, n=10` = "solid",
  `N=50, K=15, n=20` = "solid",
  `N=500,K=150, n=10` = "solid",
  `二項分布(n=10,p=0.3)` = "dashed"
)

# 5. ggplotのコード
p <- ggplot(df_long, aes(x = k, y = probability, color = parameters)) +
  geom_segment(aes(xend = k, yend = 0), linewidth = 0.8) +
  geom_point(size = 2.5) +
  geom_line(aes(linetype = parameters), linewidth = 0.7) +
  facet_wrap(~parameters, ncol = 2, scales = "fixed") +

  # x軸の目盛りを整数にする
  scale_x_continuous(breaks = function(x) floor(min(x)):ceiling(max(x))) +
  # xlim(c(0,10)) +
  scale_color_manual(values = manual_colors) +
  scale_linetype_manual(values = manual_linetypes, guide = "none") +
  guides(color = guide_legend(override.aes = list(linetype = "solid"))) +
  labs(
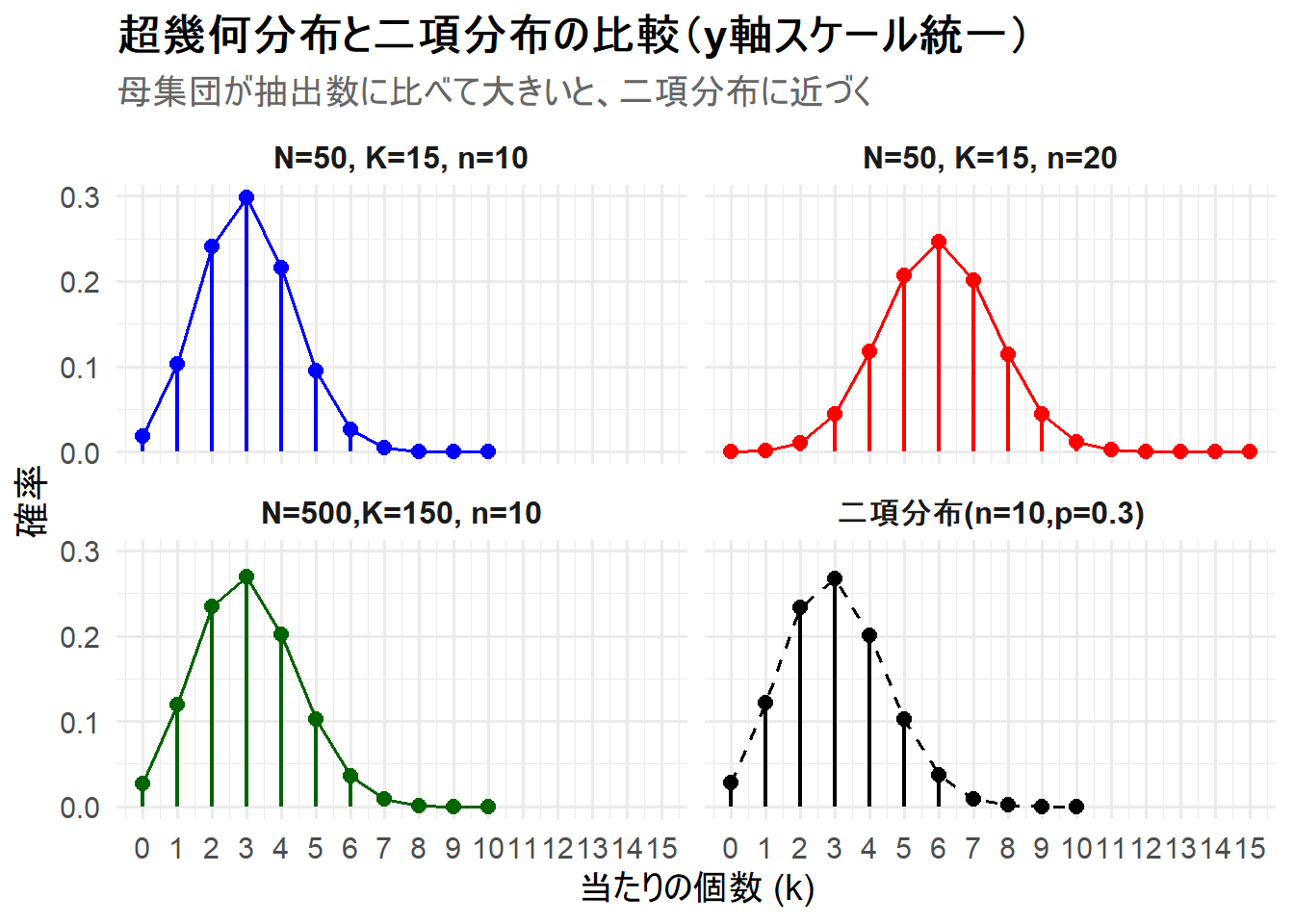
    title = "超幾何分布と二項分布の比較（y軸スケール統一）",
    subtitle = "母集団が抽出数に比べて大きいと、二項分布に近づく",
    x = "当たりの個数 (k)",
    y = "確率"
  ) +
  theme_minimal(base_size = 14) +
  theme(
    legend.position = "none",
    plot.title = element_text(face = "bold"),
    plot.subtitle = element_text(color = "gray40"),
    strip.text = element_text(face = "bold", size = 12)
  )

# チャートの表示
print(p)

Figure 1 の解説

上記のRコードを実行すると、3つの超幾何分布と1つの二項分布が描画されたチャート Figure 1 が生成されます。

N=50, K=15, n=10 (左上) と 二項分布(n=10,p=0.3) (右下) の比較:
- ピークの高さ: 超幾何分布（左上）のピーク（\(k=3\)で約0.3）は、二項分布（右下）のピーク（\(k=3\)で約0.267）よりも高くなっています。
- 裾の短さ: \(k=0\) および \(k=7\) の場合の二項分布と比較した確率は以下の通り、超幾何分布の方が二項分布より低くなっています。これは、超幾何分布が二項分布よりも平均の周りに確率が集中しており、裾が短い（ばらつきが小さい）ことを示しています。

# 1. 超幾何分布の確率を計算
prob_hyper_k0 <- dhyper(
  x = 0, # 標本中の当たりの数 (k)
  m = 15, # 母集団の当たりの総数 (K)
  n = 50 - 15, # 母集団のハズレの総数 (N-K)
  k = 10
) # 抽出する標本のサイズ (n)
prob_hyper_k7 <- dhyper(
  x = 7,
  m = 15,
  n = 50 - 15,
  k = 10
)
prob_hyper_k3 <- dhyper(
  x = 3,
  m = 15,
  n = 50 - 15,
  k = 10
)

# 2. 二項分布の確率を計算
prob_binom_k0 <- dbinom(
  x = 0, # 成功回数 (k)
  size = 10, # 試行回数 (n)
  prob = 0.3
) # 成功確率 (p)
prob_binom_k7 <- dbinom(
  x = 7,
  size = 10,
  prob = 0.3
)
prob_binom_k3 <- dbinom(
  x = 3,
  size = 10,
  prob = 0.3
)

# 3. 結果を表示
print(paste("超幾何分布 (N=50, K=15, n=10) で k=0 となる確率:", prob_hyper_k0))
print(paste("二項分布 (n=10, p=0.3) で k=0 となる確率:", prob_binom_k0))
cat("\n")
print(paste("超幾何分布 (N=50, K=15, n=10) で k=7 となる確率:", prob_hyper_k7))
print(paste("二項分布 (n=10, p=0.3) で k=7 となる確率:", prob_binom_k7))
cat("\n")
print(paste("超幾何分布 (N=50, K=15, n=10) で k=3 となる確率:", prob_hyper_k3))
print(paste("二項分布 (n=10, p=0.3) で k=3 となる確率:", prob_binom_k3))

[1] "超幾何分布 (N=50, K=15, n=10) で k=0 となる確率: 0.017871341971262"
[1] "二項分布 (n=10, p=0.3) で k=0 となる確率: 0.0282475249"

[1] "超幾何分布 (N=50, K=15, n=10) で k=7 となる確率: 0.00410007150341801"
[1] "二項分布 (n=10, p=0.3) で k=7 となる確率: 0.00900169199999999"

[1] "超幾何分布 (N=50, K=15, n=10) で k=3 となる確率: 0.297855699521034"
[1] "二項分布 (n=10, p=0.3) で k=3 となる確率: 0.266827932"

N=500,K=150, n=10 (左下) と 二項分布(n=10,p=0.3) (右下) の比較:
- この2つのグラフは、視覚的にほとんど区別がつきません。ピークの高さも、裾の広がりもほぼ同じです。
- これは、母集団のサイズ(\(N=500\))が抽出数(\(n=10\))に比べて非常に大きいため、非復元抽出の影響（有限母集団修正項 \(\frac{N-n}{N-1}\) がほぼ1になる）が無視できるほど小さくなり、超幾何分布が二項分布に収束していることを示しています。
N=50, K=15, n=20 (右上):
- 抽出数\(n\)が20と大きいため、分布の横幅が広がり、その分ピークの高さは他のケースより低くなっていることがわかります。

以上です。