Rで 重み付けカッパ係数 を確認します。
本ポストはこちらの続きです。

1. 重み付けカッパ係数(Weighted Kappa)とは
重み付けカッパ係数(\(\kappa_w\))は、評価カテゴリが順序尺度(例:悪い、普通、良い)である場合に用いられる評価者間一致度の指標です。
通常のカッパ係数では、評価の不一致はすべて等しく扱われます。例えば、「良い」を「普通」と間違えるのも、「良い」を「悪い」と間違えるのも、同じ「1つの不一致」としてカウントされます。しかし、評価カテゴリに順序がある場合、不一致の程度には「深刻さ」の違いがあるはずです。「良い」と「普通」の不一致は「軽微」ですが、「良い」と「悪い」の不一致は「深刻」です。
重み付けカッパ係数は、この不一致の深刻度に応じて重みを付け、より実態に即した一致度を計算します。
数学的定義
重み付けカッパ係数も、基本的な構造は通常のカッパ係数と同じです。
\[
\kappa_w = \dfrac{P_{o(w)} - P_{e(w)}}{1 - P_{e(w)}}
\]
違いは、観測された一致率 (\(P_o\)) と期待一致率 (\(P_e\)) の計算に重み行列 (\(W\)) を導入する点です。重み行列 \(W\) は \(k \times k\) の行列で、各要素 \(w_{ij}\) は評価者1がカテゴリ \(i\)、評価者2がカテゴリ \(j\) と評価した組み合わせに対する重みを示します。
通常、対角成分(完全に一致)の重みは \(w_{ii} = 1\) とし、非対角成分(不一致)の重みは \(0 \le w_{ij} < 1\) となります。不一致の深刻さが大きいほど、重み \(w_{ij}\) は小さくなります(0に近づく)。
a. 重み付き観測一致率 (\(P_{o(w)}\))
\(P_{o(w)}\) は、観測された各セル度数 \(n_{ij}\) に対応する重み \(w_{ij}\) を掛けて合計し、総数 \(N\) で割ることで計算されます。
\[
P_{o(w)} = \dfrac{1}{N} \displaystyle\sum_{i=1}^{k} \displaystyle\sum_{j=1}^{k} w_{ij} n_{ij}
\]
b. 重み付き期待一致率 (\(P_{e(w)}\))
\(P_{e(w)}\) は、偶然その組み合わせが起こる期待確率に重み \(w_{ij}\) を掛けて合計します。
\[
P_{e(w)} = \dfrac{1}{N^2} \displaystyle\sum_{i=1}^{k} \displaystyle\sum_{j=1}^{k} w_{ij} n_{i.} n_{.j}
\]
重みの種類
重みの付け方にはいくつか種類がありますが、代表的なものは以下の2つです。
- 線形重み (Linear weights): 不一致の距離に比例して重みを減らします。 \[ w_{ij} = 1 - \dfrac{|i-j|}{k-1} \] (例:5段階評価で「4」と「5」の不一致は、「3」と「5」の不一致より重みが大きい)
- 2乗重み (Quadratic weights): 不一致の距離の2乗に比例して重みを減らします。距離が離れるほど、ペナルティが急激に大きくなります。 \[ w_{ij} = 1 - \left( \dfrac{i-j}{k-1} \right)^2 \]
この重み付けにより、カテゴリの順序関係を考慮した、より柔軟な一致度の評価が可能になります。
2. シミュレーションのシナリオ
タイトル: 「ベテランと新人の映画評論家による5段階評価」
登場人物:
- Aさん: 映画評価の経験が長いベテラン評論家。評価は安定している。
- Bさん: デビューしたての新人評論家。まだ評価の軸が定まっていない。
ストーリー: ある映画情報サイトが、100本の新作映画のレビューを掲載することになりました。ベテランのAさんと新人のBさんが、それぞれ独立して各映画を5段階(★1: ひどい, ★2: いまいち, ★3: 普通, ★4: 良い, ★5: 傑作)で評価します。
この評価は順序尺度であり、評価のズレの大きさには意味があります。例えば、Aさんが「★4」と評価した映画をBさんが「★5」と評価する不一致は、Bさんが「★1」と評価する不一致よりも、はるかに「軽微な意見の相違」と言えます。
そこで、Bさんの評価スキルが向上する(=評価のばらつきが小さくなる)につれて、Aさんとの評価の一致度がどう変化するかをシミュレートします。このとき、「ズレの大きさを考慮しない通常のカッパ係数」と、「ズレの大きさを考慮する重み付けカッパ係数」の両方を計算し、その違いを比較します。
シミュレーションの設計:
- 100本の映画の「真の評価(1〜5の5段階)」をランダムに生成します。
- Aさんの評価は、「真の評価」に対して小さなばらつき(標準偏差0.5)で生成します。
- Bさんの評価のばらつき(標準偏差)を、大きな値(2.0)から小さな値(0.5)まで変化させていきます。これはBさんのスキル向上を模倣しています。
- 各ばらつきのレベルで、AさんとBさんの評価結果をシミュレートします。
- 通常のカッパ係数と、2乗重みを用いた重み付けカッパ係数を計算します。
- このプロセスを何度も繰り返し、Bさんの評価のばらつきと2種類のカッパ係数の関係をグラフで可視化します。
3. R言語によるシミュレーションコード
以下に、上記のシナリオに基づいた重み付けカッパ係数のシミュレーションコードを記述します。
# 必要なライブラリを読み込む
library(dplyr)
library(ggplot2)
library(irr) # カッパ係数の計算に利用
library(tidyr)
# シミュレーションのパラメータ設定
seed <- 20250806
set.seed(seed) # 結果の再現性をための乱数シード
num_movies <- 100 # 映画の本数
categories <- 1:5 # 評価カテゴリ(1から5)
sd_A <- 0.5 # Aさん(ベテラン)の評価のばらつき(標準偏差)
# Bさん(新人)の評価のばらつきを変化させる
sd_B_levels <- seq(2.0, 0.5, by = -0.1)
num_simulations <- 100 # 各ばらつきレベルでのシミュレーション回数
# シミュレーション結果を格納するためのデータフレームを初期化
simulation_results <- data.frame()
# Bさんの各ばらつきレベルでシミュレーションを実行
for (sd_B in sd_B_levels) {
for (i in 1:num_simulations) {
# 1. 真の評価を生成(平均3、標準偏差1.5の正規分布に従うとする)
true_rating_raw <- rnorm(num_movies, mean = 3, sd = 1.5)
# 評価を1〜5の整数に丸めてクリッピング
true_rating <- round(pmax(min(categories), pmin(max(categories), true_rating_raw)))
# 2. Aさんの評価をシミュレート
rating_A_raw <- true_rating + rnorm(num_movies, mean = 0, sd = sd_A)
rating_A <- round(pmax(min(categories), pmin(max(categories), rating_A_raw)))
# 3. Bさんの評価をシミュレート
rating_B_raw <- true_rating + rnorm(num_movies, mean = 0, sd = sd_B)
rating_B <- round(pmax(min(categories), pmin(max(categories), rating_B_raw)))
# 4. 2種類のカッパ係数を計算
ratings_df <- data.frame(A = rating_A, B = rating_B)
# 通常のカッパ係数(重みなし)
kappa_unweighted <- kappa2(ratings_df, weight = "unweighted")$value
# 重み付けカッパ係数(2乗重み)
kappa_weighted <- kappa2(ratings_df, weight = "squared")$value
# 結果を一時的に保存
temp_result <- data.frame(
sd_B = sd_B,
simulation_run = i,
unweighted_kappa = kappa_unweighted,
weighted_kappa = kappa_weighted
)
# シミュレーション結果を結合
simulation_results <- rbind(simulation_results, temp_result)
}
}
# シミュレーション結果の要約
summary_results <- simulation_results %>%
group_by(sd_B) %>%
summarise(
mean_unweighted_kappa = mean(unweighted_kappa),
mean_weighted_kappa = mean(weighted_kappa),
.groups = "drop"
)
# プロット用にデータを縦長形式に変換
plot_data <- summary_results %>%
pivot_longer(
cols = c("mean_unweighted_kappa", "mean_weighted_kappa"),
names_to = "kappa_type",
values_to = "kappa_value"
) %>%
mutate(kappa_type_jp = case_when(
kappa_type == "mean_unweighted_kappa" ~ "通常カッパ",
kappa_type == "mean_weighted_kappa" ~ "重み付けカッパ"
))
# 結果の出力
print(summary_results)
# ggplot2による結果の可視化
p <- ggplot(plot_data, aes(x = sd_B, y = kappa_value, color = kappa_type_jp)) +
geom_line(linewidth = 1.2) +
geom_point(size = 2.5) +
scale_x_reverse() + # 横軸を反転させ、右に行くほどスキル向上するように見せる
scale_color_manual(values = c("通常カッパ" = "darkorange", "重み付けカッパ" = "dodgerblue")) +
labs(
title = "新人評論家のスキル向上と2種類のカッパ係数の比較",
subtitle = "評価の「ズレの大きさ」を考慮する重み付けカッパ係数の効果",
x = "新人Bさんの評価のばらつき(標準偏差)※小さいほど高スキル",
y = "カッパ係数(平均値)",
color = "カッパ係数の種類",
caption = "各ばらつきレベルで100回のシミュレーションを実施した結果"
) +
theme_minimal(base_size = 14) +
theme(
plot.title = element_text(face = "bold", size = 18),
plot.subtitle = element_text(size = 12),
axis.title = element_text(face = "bold"),
legend.position = "bottom",
legend.title = element_text(face = "bold"),
plot.caption = element_text(color = "grey40")
)
# プロットを表示
print(p)# A tibble: 16 × 3
sd_B mean_unweighted_kappa mean_weighted_kappa
<dbl> <dbl> <dbl>
1 0.5 0.475 0.847
2 0.6 0.414 0.820
3 0.7 0.374 0.797
4 0.8 0.345 0.779
5 0.9 0.316 0.740
6 1 0.284 0.723
7 1.1 0.267 0.693
8 1.2 0.237 0.661
9 1.3 0.231 0.634
10 1.4 0.215 0.609
11 1.5 0.195 0.579
12 1.6 0.179 0.553
13 1.7 0.162 0.525
14 1.8 0.165 0.502
15 1.9 0.158 0.488
16 2 0.157 0.478シミュレーション結果の解説
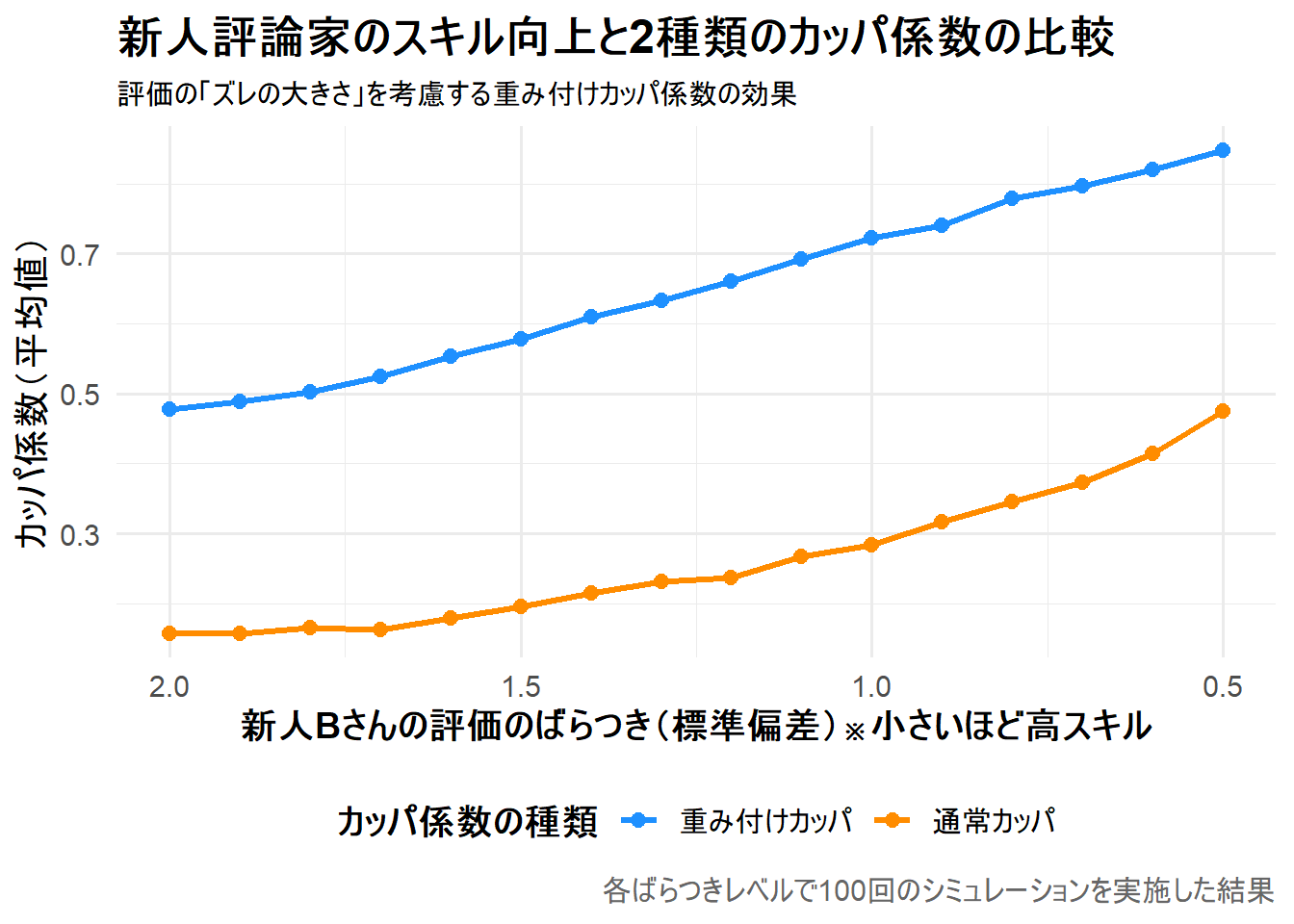
上記の表と Figure 1 は、新人Bさんの評価のばらつき(sd_B)が小さくなる(スキルが向上する)につれて、通常カッパ係数と重み付けカッパ係数がどのように変化するかを示しています。
注目すべきは、常に重み付けカッパ係数の方が高い値を示している点です。
これは、評価のズレが小さい不一致(例:★4と★5)を部分的な一致として許容するためです。
特に、Bさんの評価のばらつきが大きい場合でも、重み付けカッパは一定の評価を与えていることがわかります。
Figure 1 は、横軸に新人Bさんの評価のばらつき(標準偏差)、縦軸にカッパ係数の平均値を示しています。横軸は反転させており、右に行くほどばらつきが小さく(=スキルが高い)ことを表します。
- 2本の線の違い: 青い線(重み付けカッパ)は、常にオレンジの線(通常カッパ)よりも上にあります。これは、重み付けカッパが「少しのズレ」を部分的な一致と見なすため、評価が甘くなる(値が高くなる)ことを示しています。
- スキルが低い領域(左側): Bさんの評価のばらつきが大きい場合、評価が大きくズレる(例:「★5」を「★2」と評価する)ことも頻発します。通常カッパはこれを単純な不一致として扱うため、値がかなり低くなります。一方、重み付けカッパは、たまたまズレが小さかった場合を評価するため、通常カッパよりは高い値を維持します。
- スキルが高い領域(右側): Bさんのスキルが向上し、Aさんと同様に評価のばらつきが小さくなると、両者の評価は頻繁に一致、あるいは1段階ズレる程度になります。この「1段階のズレ」を通常カッパは「完全な不一致」としますが、重み付けカッパは「ほぼ一致」と見なします。そのため、両者の差は依然として大きく、重み付けカッパは「実質的にはよく一致している」という実態をより適切に反映した高い値(0.8以上)を示します。
このシミュレーションから、順序尺度を持つデータを評価する際には、重み付けカッパ係数を用いることで、単なる一致/不一致ではなく「どの程度意見が近いか」という、より現実に即した評価者間の一致度を測定できることがわかります。
以上です。