Rの関数から transfer_entropy {RTransferEntropy} を確認します。
1. トランスファーエントロピーとは?
トランスファーエントロピー(Transfer Entropy, TE)は、ある時系列から別の時系列へ、どれだけの情報が流れているかを定量化する指標です。情報理論における「シャノンエントロピー」の概念を応用したものです。
簡単に言えば、「時系列Yの将来の値を予測する際に、Y自身の過去の情報だけを使う場合に比べて、時系列Xの過去の情報を追加することで、予測の不確実性がどれだけ減少するか?」を測ります。
この「不確実性の減少量」がトランスファーエントロピーであり、この値が大きいほど、XからYへの情報の流れ(情報的因果性)が強いと解釈できます。
グレンジャー因果性検定との違い
- グレンジャー因果性検定: 変数間の線形の関係を前提としています。つまり、Xの過去の値がYの将来の値を「線形的に」予測するのに役立つかを検定します。
- トランスファーエントロピー: 特定のモデルを仮定しないノンパラメトリックな手法です。そのため、変数間の非線形な関係性や、より複雑な依存関係も捉えることができます。
2. transfer_entropy 関数の引数解説
transfer_entropy関数は多くの引数を持ちますが、主要なものを以下に解説します。
transfer_entropy(x, y,
lx = 1, ly = 1, q = 0.1, entropy = "Shannon",
shuffles = 100, type = "quantiles", quantiles = c(5, 95),
bins = NULL, limits = NULL, nboot = 300, burn = 50,
quiet = NULL, seed = NULL, na.rm = TRUE
)| 引数 | 説明 |
|---|---|
x, y | 分析対象の2つの時系列データ(数値ベクトル)。xからyへの流れ(X->Y)と、yからxへの流れ(Y->X)の両方が計算されます。 |
lx, ly | それぞれxとyの過去の履歴として考慮するラグの数。マルコフ過程の次数に相当します。例えば lx=2 は x(t-1) と x(t-2) を考慮することを意味します。 |
entropy | 計算の基礎となるエントロピーの種類。“Shannon”(シャノンエントロピー、デフォルト)または”Renyi”(レニーエントロピー)を選択できます。 |
q | entropy = "Renyi" の場合に指定するパラメータ(0 < q < 1)。 |
shuffles | 有効トランスファーエントロピー(Effective Transfer Entropy, ETE)を計算するためのシャッフル回数。時系列をランダムに並び替えてTEを計算し、元のTEからその平均値を差し引くことで、有限データサイズによるバイアスやノイズの影響を補正します。結果を解釈する上で重要です。 |
type | 連続値データを離散的な状態に変換(ビン化)する方法。TEは確率を計算するため、この処理が必要です。“quantiles”, “bins”, “limits”から選択します。 |
quantiles | type="quantiles"の時に使用。データを区切るパーセンタイルをベクトルで指定します。例: c(5, 95)は、データを下位5%、中間90%、上位5%の3つの状態に分割します。外れ値に強い方法です。 |
bins | type="bins"の時に使用。データを等間隔に分割する際のビンの(状態の)数を指定します。 |
limits | type="limits"の時に使用。データを分割するための具体的な閾値をベクトルで指定します。 |
nboot | ブートストラップのリサンプリング回数。計算されたETEの統計的有意性を評価(p値の計算)するために使用します。0より大きい値を指定すると、標準誤差とp値が計算されます。 |
seed | 乱数シード。結果の再現性を確保したい場合に使用します。 |
3. トランスファーエントロピーのシミュレーション
ここでは、グレンジャー因果性検定では検出できないが、トランスファーエントロピーでは検出できる非線形な因果関係を持つデータを生成し、両者の違いを比較します。
シナリオ: 時系列 x の過去の値の 2乗 が、時系列 y の現在の値に影響を与える。
3.1. 準備
まず、必要なパッケージを読み込みます。
library(RTransferEntropy)
library(lmtest)
library(ggplot2)
library(styler)3.2. 非線形関係を持つ時系列データの生成
時系列yを、自身の1期前の値と、xの1期前の値の2乗に依存するように、つまり非線形の関係にある2つの時系列サンプルデータを生成します。
# 再現性のための乱数シード設定
seed <- 20250829
set.seed(seed)
# データ生成
n_obs <- 1000 # 観測数
x <- rnorm(n_obs) # xはホワイトノイズ
y <- numeric(n_obs) # yを格納するベクトル
# yの生成: y[t] = 0.3*y[t-1] + 1.2 * x[t-1]^2 + noise
for (t in 2:n_obs) {
y[t] <- 0.3 * y[t - 1] + 1.2 * (x[t - 1])^2 + rnorm(1, sd = 0.8)
}
# 最初の値を削除して定常性を高める
x <- x[-1]
y <- y[-1]
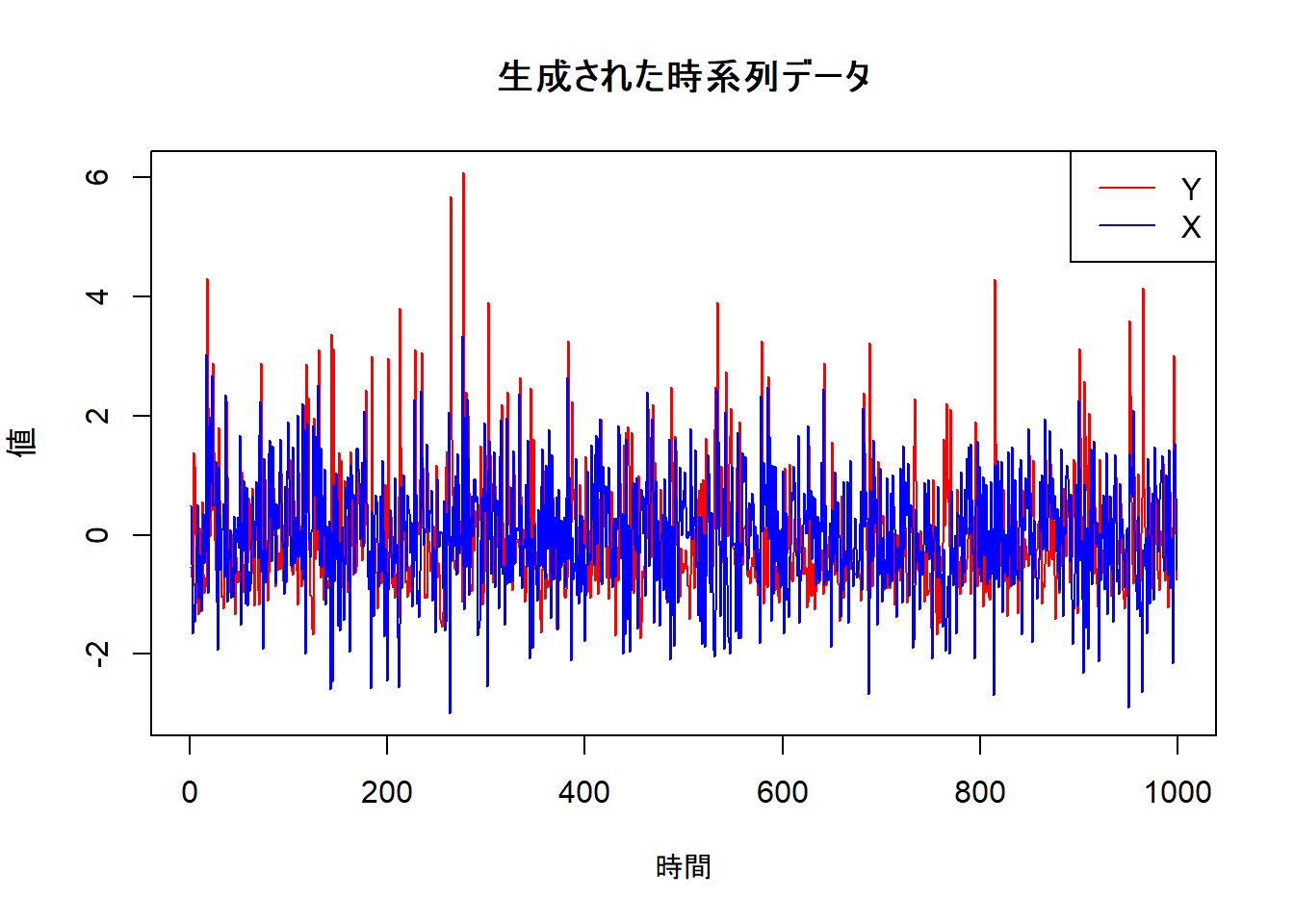
# 生成したデータの可視化
df_plot <- data.frame(
time = 1:length(x),
x = scale(x), # 標準化して見やすくする
y = scale(y)
)
plot(df_plot$time, df_plot$y,
type = "l", col = "red", ylim = range(c(df_plot$x, df_plot$y)),
main = "生成された時系列データ", xlab = "時間", ylab = "値"
)
lines(df_plot$time, df_plot$x, type = "l", col = "blue")
legend("topright", legend = c("Y", "X"), col = c("red", "blue"), lty = 1)3.3. グレンジャー因果性検定の実行
まず、lmtest::grangertest を用いて、xがyのグレンジャー原因となっているかを検定します。
cat("--- グレンジャー因果性検定 (X -> Y) ---\n")
granger_xy <- grangertest(y ~ x, order = 1)
print(granger_xy)
# 念のため逆方向も確認
cat("\n--- グレンジャー因果性検定 (Y -> X) ---\n")
granger_yx <- grangertest(x ~ y, order = 1)
print(granger_yx)--- グレンジャー因果性検定 (X -> Y) ---
Granger causality test
Model 1: y ~ Lags(y, 1:1) + Lags(x, 1:1)
Model 2: y ~ Lags(y, 1:1)
Res.Df Df F Pr(>F)
1 995
2 996 -1 0.2969 0.586
--- グレンジャー因果性検定 (Y -> X) ---
Granger causality test
Model 1: x ~ Lags(x, 1:1) + Lags(y, 1:1)
Model 2: x ~ Lags(x, 1:1)
Res.Df Df F Pr(>F)
1 995
2 996 -1 0.3192 0.5722X -> Yの検定結果を見ると、p値は 0.586と、有意水準5%で「xはyのグレンジャー原因ではない」という帰無仮説を棄却できません。これは、グレンジャー因果性検定が両者間の線形予測関係しか見ていないため、存在する非線形の因果関係を検出できなかったことを示しています。
3.4. トランスファーエントロピーの計算
次に、RTransferEntropy::transfer_entropy を用いて、同じデータ間の情報フローを測定します。
cat("\n--- トランスファーエントロピーの計算 ---\n")
te_results <- transfer_entropy(
x = x,
y = y,
lx = 1, # xのラグ
ly = 1, # yのラグ
nboot = 200, # ブートストラップ回数 (p値計算用)
shuffles = 100, # ETE計算用のシャッフル回数
seed = seed # 再現性のため
)
# 結果の表示
print(te_results)
--- トランスファーエントロピーの計算 ---
Shannon's entropy on 1 core with 100 shuffles.
x and y have length 999 (0 NAs removed)
[calculate] X->Y transfer entropy
[calculate] Y->X transfer entropy
[bootstrap] 200 times
Done - Total time 15.28 seconds
Shannon Transfer Entropy Results:
-----------------------------------------------------------
Direction TE Eff. TE Std.Err. p-value sig
-----------------------------------------------------------
X->Y 0.1904 0.1837 0.0031 0.0000 ***
Y->X 0.0063 0.0000 0.0032 0.5050
-----------------------------------------------------------
Bootstrapped TE Quantiles (200 replications):
-----------------------------------------------------------
Direction 0% 25% 50% 75% 100%
-----------------------------------------------------------
X->Y 0.0008 0.0040 0.0057 0.0079 0.0208
Y->X 0.0019 0.0046 0.0064 0.0091 0.0171
-----------------------------------------------------------
Number of Observations: 999
-----------------------------------------------------------
p-values: < 0.001 '***', < 0.01 '**', < 0.05 '*', < 0.1 '.' Shannon Transfer Entropy Results テーブル
こちらが分析のメインとなる結果です。
-----------------------------------------------------------
Direction TE Eff. TE Std.Err. p-value sig
-----------------------------------------------------------
X->Y 0.1904 0.1837 0.0031 0.0000 ***
Y->X 0.0063 0.0000 0.0032 0.5050
-----------------------------------------------------------| 列名 | 説明 |
|---|---|
Direction | 情報フローの方向を示します。「X->Y」はXからYへ、「Y->X」はYからXへの流れを意味します。 |
TE | トランスファーエントロピー(Transfer Entropy)の生の計算値です。 |
Eff. TE | 有効トランスファーエントロピー(Effective Transfer Entropy)。生のTEから、データをシャッフルして計算したTEの平均値(ノイズや偶然によるバイアス)を差し引いたものです。解釈の中心となる最も重要な指標です。 この値が0より大きい場合、バイアスを考慮してもなお情報フローが存在することを示唆します。 |
Std.Err. | Eff. TE の標準誤差です。ブートストラップ法によって計算され、推定値のばらつき(信頼性)を示します。 |
p-value | Eff. TE が統計的に有意に0より大きいかどうかを検定した結果のp値です。帰無仮説は「情報フローは存在しない(Eff. TE = 0)」です。この値が有意水準(例: 0.05)より小さい場合、帰無仮説は棄却され、統計的に有意な情報フローが存在すると結論付けられます。 |
sig | p値に応じた有意性コード(***, **, *, .)で、結果を視覚的に分かりやすく示します。 |
Bootstrapped TE Quantiles テーブル
このテーブルは、p値を計算する背景となるブートストラップ(シャッフル)の結果の分布を示しています。これは「もし時系列間に本当の関係がなかったら、TEはどのような値をとるか」というシミュレーションの結果です。
-----------------------------------------------------------
Direction 0% 25% 50% 75% 100%
-----------------------------------------------------------
X->Y 0.0008 0.0040 0.0057 0.0079 0.0208
Y->X 0.0019 0.0046 0.0064 0.0091 0.0171
-----------------------------------------------------------このテーブルを見ることで、観測されたTEの値が、偶然によって生じる値の範囲(つまり、このテーブルに示された値の範囲)からどれだけ外れているかを確認できます。
XからYへの情報フロー (X->Y)
- 有効トランスファーエントロピー (
Eff. TE) は 0.1837 と、正の値を示しています。これは、ノイズ等の影響を補正した後でも、XからYへの実質的な情報フローが存在することを示しています。 - p値 (
p-value) は 0.0000 と、有意(5%)に「XからYへの情報フローは存在しない」という帰無仮説は棄却されます。 - 結論: XからYへの有意な情報の流れが検出されました。
- 補足:
Bootstrapped TE Quantilesテーブルを見ると、実際に観測されたX->Y方向のTEは0.1904ですが、同じ方向のシャッフルデータから得られたTEは最大でも0.0208であることが確認できます。
YからXへの情報フロー (Y->X)
- 有効トランスファーエントロピー (
Eff. TE) は 0.0000 です。これは、観測された生のTE (0.0063) は、データのシャッフルによって生じるバイアス(ノイズ)の範囲内であり、実質的な情報フローはゼロであると判断されたことを意味します。 - p値 (
p-value) は 0.5050 であり、有意水準(5%)を超えています。したがって、「YからXへの情報フローは存在しない」という帰無仮説を棄却することはできません。 - 結論: YからXへの有意な情報の流れは検出されませんでした。
- 補足:
Bootstrapped TE Quantilesテーブルを見ると、Y->X方向で観測された生のTE0.0063は、シャッフルによって得られたTEの分布(0%点0.0019、100%点0.0171、中央値0.0064)の中央値近くに位置しています。これは、観測されたTEが偶然の結果である可能性が高いことを示しています。
以上です。