Rで カッパ係数 を確認します。
1. カッパ係数(Cohen’s Kappa)とは
カッパ係数(\(\kappa\))は、2人の評価者(rater)が対象を分類する際に、その評価がどの程度一致しているかを示す指標です。偶然の一致を考慮している点が、単純な一致率(accuracy)と大きく異なります。
評価者が \(k\) 個のカテゴリに \(N\) 個の対象を分類する場合を考えます。評価結果は以下のような \(k \times k\) の分割表(contingency table)で表せます。
| 評価者2: Cat 1 | 評価者2: Cat 2 | … | 評価者2: Cat k | 合計 | |
|---|---|---|---|---|---|
| 評価者1: Cat 1 | \(n_{11}\) | \(n_{12}\) | … | \(n_{1k}\) | \(n_{1.}\) |
| 評価者1: Cat 2 | \(n_{21}\) | \(n_{22}\) | … | \(n_{2k}\) | \(n_{2.}\) |
| … | … | … | … | … | … |
| 評価者1: Cat k | \(n_{k1}\) | \(n_{k2}\) | … | \(n_{kk}\) | \(n_{k.}\) |
| 合計 | \(n_{.1}\) | \(n_{.2}\) | … | \(n_{.k}\) | \(N\) |
ここで、\(n_{ij}\) は評価者1がカテゴリ \(i\)、評価者2がカテゴリ \(j\) と評価した対象の数、\(n_{i.}\) は評価者1がカテゴリ \(i\) と評価した合計数、\(n_{.j}\) は評価者2がカテゴリ \(j\) と評価した合計数です。
カッパ係数は、以下の式で定義されます。
\[
\kappa = \dfrac{P_o - P_e}{1 - P_e}
\]
各項の意味は以下の通りです。
a. 観測された一致率 (\(P_o\))
\(P_o\) (Observed Agreement)は、2人の評価者の判断が実際に一致した割合です。分割表の対角成分の合計を総数 \(N\) で割ることで計算されます。
\[
P_o = \dfrac{\displaystyle\sum_{i=1}^{k} n_{ii}}{N}
\]
b. 偶然による期待一致率 (\(P_e\))
\(P_e\) (Expected Agreement)は、2人の評価者が完全にランダムに評価した場合に、偶然評価が一致する期待確率です。各カテゴリについて、評価者1がそのカテゴリを選ぶ確率と評価者2がそのカテゴリを選ぶ確率の積を計算し、それらを全カテゴリで合計します。
評価者1がカテゴリ \(i\) を選ぶ確率は \(\dfrac{n_{i.}}{N}\)、評価者2がカテゴリ \(i\) を選ぶ確率は \(\dfrac{n_{.i}}{N}\) と推定されます。したがって、\(P_e\) は次のように計算されます。
\[
P_e = \displaystyle\sum_{i=1}^{k} \left( \dfrac{n_{i.}}{N} \times \dfrac{n_{.i}}{N} \right)
\]
カッパ係数の解釈
- \(\kappa = 1\): 評価者が完全に一致している。
- \(\kappa > 0\): 偶然期待されるよりも一致率が高い。
- \(\kappa = 0\): 偶然期待される一致率と等しい(評価はランダム)。
- \(\kappa < 0\): 偶然期待されるよりも一致率が低い(稀なケース)。
一般的に、Landis & Koch (1977) による以下の解釈が広く用いられます。
- 0.81 – 1.00: ほぼ完全な一致 (Almost perfect)
- 0.61 – 0.80: かなりの一致 (Substantial)
- 0.41 – 0.60: 中程度の一致 (Moderate)
- 0.21 – 0.40: まあまあの一致 (Fair)
- 0.00 – 0.20: わずかな一致 (Slight)
- < 0.00: 一致しない (Poor)
2. シミュレーションのシナリオ
タイトル: 「ベテラン放射線科医と新人研修医のレントゲン画像診断」
登場人物:
- 医師A: 経験豊富なベテラン放射線科医。診断精度は非常に高い。
- 医師B: 研修中の新人放射線科医。診断精度はまだ発展途上。
ストーリー: ある病院で、100人の患者の胸部レントゲン画像を使い、新人研修医(医師B)の診断能力を評価することになりました。比較対象として、その道のプロであるベテラン(医師A)にも同じ100枚の画像を診断してもらいます。診断内容は、特定の疾患の「陽性」か「陰性」かの2択です。
私たちは、医師Bのスキルが向上するにつれて、医師Aとの診断の一致度がどのように変化するかをシミュレーションで確認したいと考えています。単純な一致率だけではなく、「偶然の一致」を除外したカッパ係数を用いて、より本質的な評価の一致度を測定します。
シミュレーションの設計:
- 100人の患者の「真の状態(真の陽性/陰性)」をランダムに生成します(例:陽性率30%)。
- 医師Aの診断精度は95%で固定します。つまり、95%の確率で「真の状態」と同じ診断を下します。
- 医師Bの診断精度を、ランダムな推測レベル(50%)からベテランレベル(95%)まで変化させていきます。
- 各精度のレベルで、医師Aと医師Bの診断結果をシミュレートし、カッパ係数を計算します。
- このプロセスを何度も繰り返し(例:各精度レベルで100回)、医師Bの精度とカッパ係数の関係をグラフで可視化します。
このシミュレーションにより、「医師Bのスキルが上がると、医師Aとのカッパ係数がどのように上昇していくか」を具体的に理解することができます。
3. R言語によるシミュレーションコード
以下に、上記のシナリオに基づいたRのシミュレーションコードを記述します。
# 必要なライブラリを読み込む
library(dplyr)
library(ggplot2)
library(irr) # カッパ係数の計算に利用
# シミュレーションのパラメータ設定
seed <- 20250805
set.seed(seed) # 結果の再現性をための乱数シード
num_patients <- 100 # 患者の数
true_positive_prop <- 0.3 # 真の陽性率
accuracy_A <- 0.95 # 医師A(ベテラン)の診断精度
# 医師B(新人)の診断精度を50%から95%まで5%刻みで変化させる
accuracy_B_levels <- seq(0.50, 0.95, by = 0.05)
num_simulations <- 100 # 各精度レベルでのシミュレーション回数
# シミュレーション結果を格納するためのデータフレームを初期化
simulation_results <- data.frame()
# 医師Bの各精度レベルでシミュレーションを実行
for (acc_B in accuracy_B_levels) {
# 各精度レベルで複数回シミュレーションを行い、結果を安定させる
for (i in 1:num_simulations) {
# 1. 真の状態を生成
# rbinomを使い、1=陽性, 0=陰性とする
true_status <- rbinom(num_patients, 1, true_positive_prop)
# 2. 医師Aの診断をシミュレート
# 医師Aが間違う確率 (1 - accuracy_A)
# 医師Aの診断 = 真の状態 XOR 間違い(1) or 正解(0)
mistake_A <- rbinom(num_patients, 1, 1 - accuracy_A)
rating_A <- true_status != mistake_A
# 3. 医師Bの診断をシミュレート
mistake_B <- rbinom(num_patients, 1, 1 - acc_B)
rating_B <- true_status != mistake_B
# 4. カッパ係数を計算
# irr::kappa2()関数は、評価者を列にしたデータフレームを要求する
ratings_df <- data.frame(A = rating_A, B = rating_B)
# 欠損値がない完全なケースのみを使用
kappa_result <- kappa2(ratings_df, weight = "unweighted")
# 結果を一時的に保存
temp_result <- data.frame(
accuracy_B = acc_B,
simulation_run = i,
kappa_value = kappa_result$value
)
# シミュレーション結果を結合
simulation_results <- rbind(simulation_results, temp_result)
}
}
# シミュレーション結果の要約
# 医師Bの各精度レベルで、カッパ係数の平均値を計算
summary_results <- simulation_results %>%
group_by(accuracy_B) %>%
summarise(mean_kappa = mean(kappa_value), .groups = "drop")
# 結果の出力
cat("--- シミュレーション結果 ---\n\n")
print(summary_results)
# ggplot2による結果の可視化
p <- ggplot(summary_results, aes(x = accuracy_B, y = mean_kappa)) +
geom_line(aes(group = 1), color = "dodgerblue", linewidth = 1.2) +
geom_point(color = "dodgerblue", size = 3) +
scale_x_continuous(labels = scales::percent_format(accuracy = 1)) +
labs(
title = "新人医師のスキル向上とカッパ係数の関係",
subtitle = "ベテラン医師(精度95%)とのレントゲン診断一致度",
x = "新人医師Bの診断精度",
y = "カッパ係数(平均値)",
caption = "各精度レベルで100回のシミュレーションを実施した結果"
) +
theme_minimal(base_size = 14) +
theme(
plot.title = element_text(face = "bold", size = 18),
plot.subtitle = element_text(size = 12),
axis.title = element_text(face = "bold"),
plot.caption = element_text(color = "grey40")
)
# プロットを表示
print(p)--- シミュレーション結果 ---
# A tibble: 10 × 2
accuracy_B mean_kappa
<dbl> <dbl>
1 0.5 -0.00000595
2 0.55 0.0805
3 0.6 0.154
4 0.65 0.234
5 0.7 0.322
6 0.75 0.394
7 0.8 0.488
8 0.85 0.587
9 0.9 0.674
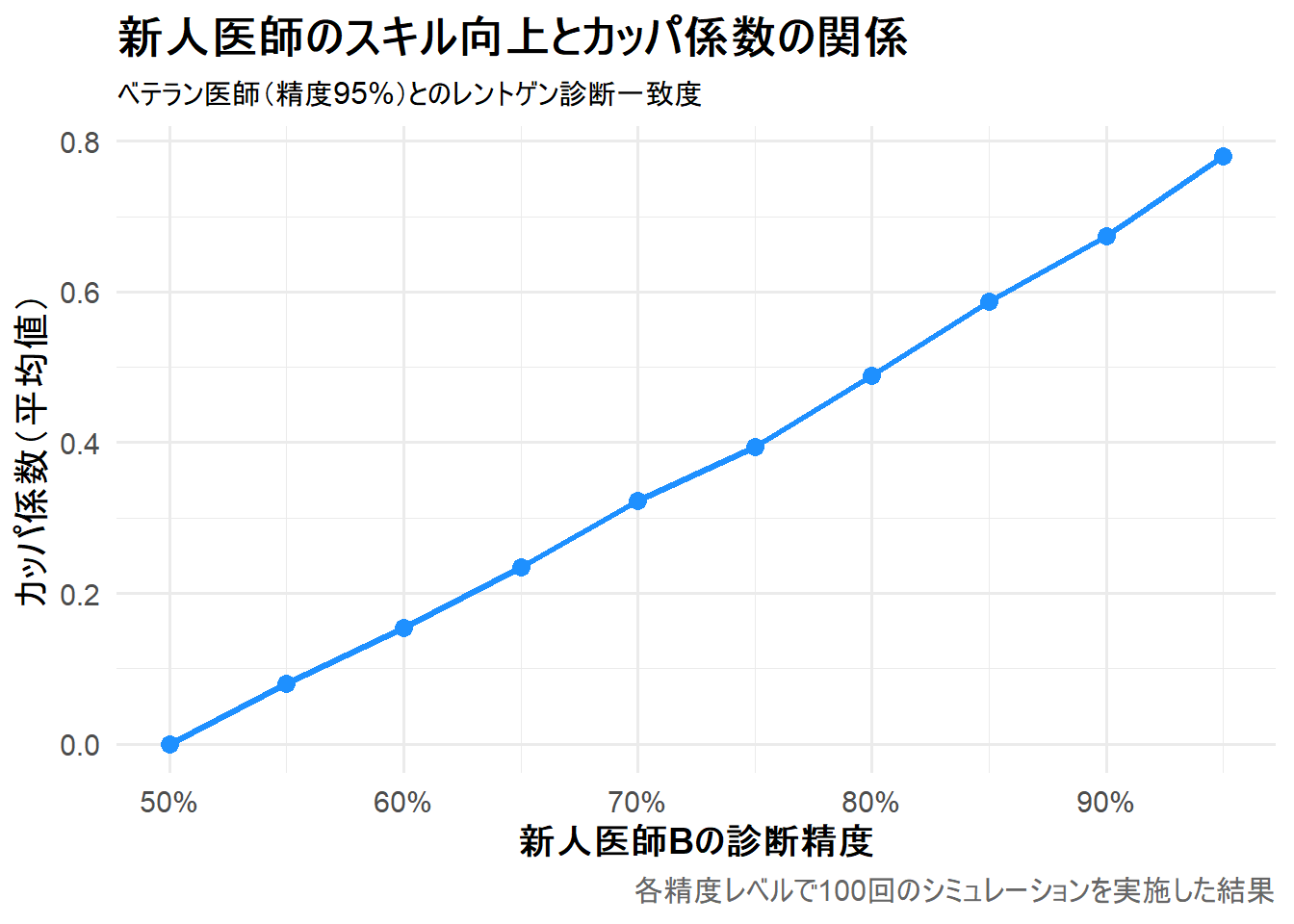
10 0.95 0.780 シミュレーション結果の解説
シミュレーション結果(summary_results)は、新人医師Bの診断精度(accuracy_B)が向上するにつれて、ベテラン医師Aとの間の一致度を示すカッパ係数の平均値(mean_kappa)がどのように変化するかを示しています。
医師Bの精度が50%(ランダム)の時、カッパ係数はほぼ0に近くなり、精度が医師Aの95%に近づくにつれて、カッパ係数が上昇していることがわかります。
Figure 1 は、横軸に新人医師Bの診断精度、縦軸に医師Aとの間で計算されたカッパ係数の平均値を示しています。
- 医師Bの精度が50%の時: これは医師Bが完全に当てずっぽうで診断している状態です。カッパ係数はほぼ0となり、「偶然以上の一致は見られない」という結果を正しく示しています。
- 精度が上がるにつれて: 医師Bの診断精度が向上する(=真の状態をより正確に捉えられるようになる)と、必然的に医師A(精度95%)との診断も一致しやすくなります。この一致はもはや偶然ではないため、カッパ係数は上昇していきます。
- 医師Bの精度が95%の時: 医師Aとほぼ同等のスキルレベルに達した時、カッパ係数は0.78となり、「かなりの一致 (Substantial)」のレベルに達します。
以上です。