Rでバークソンのパラドックス

Rで バークソンのパラドックス を試みます。

1. 「バークソンのパラドックス」とは

バークソンのパラドックス（Berkson’s Paradox）とは、統計学における選択バイアスの一種です。実際には独立している（相関がない）2つの事象が、特定の条件下で抽出された集団（サンプル）だけを観察すると、あたかも負の相関があるかのように見えてしまう現象を指します。

このパラドックスの鍵は「特定の条件下で抽出された集団」という点にあります。この「選択」という行為そのものが、見かけ上の相関を生み出してしまいます。

分かりやすい例：レストラン選び

ある街にたくさんのレストランがあり、レストランの評価軸が「味」と「雰囲気」の2つだとします。そして、街全体で見れば、「味」と「雰囲気」には特に関係がない（独立している）と仮定します。つまり、味が良いからといって雰囲気が良いとは限らず、その逆もまた然りです。

しかし、あなたがレストランを選ぶとき、無意識に次のような基準で選んでいるとします。「味がすごく良いまたは雰囲気がすごく良いレストランに行きたい」

この基準を満たさない「味がそこそこで、雰囲気もそこそこの店」や「味も雰囲気も悪い店」は、あなたの選択肢から外れます。

その結果、あなたがこれまで行ったことのあるレストランのリスト（＝選択された集団）を振り返ると、次のような傾向が見られるはずです。

「すごく味が良い店」は、雰囲気がそれほど良くなくてもあなたの基準をクリアしているのでリストに入っている。
「すごく雰囲気が良い店」は、味がそれほど良くなくてもあなたの基準をクリアしているのでリストに入っている。

このリストの中だけで「味」と「雰囲気」の関係を見ると、「味が良い店は雰囲気がいまいち」で、「雰囲気が良い店は味がいまいち」という見かけ上の負の相関が生まれてしまいます。これがバークソンのパラドックスです。

実際には街全体には「味も雰囲気も良い店」はたくさんあるのですが、あなたの選択基準によって、その関係性が歪んで見えてしまうのです。

2. R言語によるシミュレーション

このパラドックスをR言語でシミュレーションしてみましょう。ここでは「俳優の才能」と「人柄の良さ」を例にします。

仮定: 全体の俳優候補者の中では、「才能」と「人柄」は独立している（相関がない）。
選択バイアス: 映画監督は、「才能が非常に優れている」または「人柄が非常に良い」候補者のみをオーディションに呼ぶ。

このシミュレーションを通して、オーディションに呼ばれた俳優たち（選択された集団）だけを見ると、「才能」と「人柄」に負の相関が見られることを確認します。

Rコード

# 必要なパッケージをインストール（可視化のため）
library(ggplot2)

# シミュレーションの再現性を確保するために乱数シードを設定
seed <- 20250809
set.seed(seed)

# 1. パラメータ設定
n <- 3000 # 全体の候補者の数
mean_score <- 50
sd_score <- 15

# 2. 全体集団（相関ゼロ）の生成
population <- data.frame(
  talent = rnorm(n, mean = mean_score, sd = sd_score),
  personality = rnorm(n, mean = mean_score, sd = sd_score)
)
cor_population <- cor(population$talent, population$personality)

# 3. 選択バイアスの適用（サンプリング）
selection_threshold <- 65 # 才能または人柄が65点以上の候補者を呼ぶ
selected_sample <- subset(population, talent > selection_threshold | personality > selection_threshold)
cor_selected <- cor(selected_sample$talent, selected_sample$personality)

# 4. 比較のための可視化
# 全体集団と選択された集団を重ね、それぞれの回帰直線を引く
p_combined_reg <- ggplot(population, aes(x = talent, y = personality)) +
  # --- 点のプロット ---
  geom_point(alpha = 0.3, color = "orange") + # 全体集団
  geom_point(data = selected_sample, aes(x = talent, y = personality), color = "blue", alpha = 0.9, shape = 2) + # 選択された集団

  # --- 回帰直線の追加 ---
  # aes()内で色分けを指定することで凡例を自動生成
  geom_smooth(aes(color = "全体集団"), method = "lm", se = FALSE, linewidth = 1) +
  geom_smooth(data = selected_sample, aes(color = "選択された集団"), method = "lm", se = FALSE, linewidth = 1) +

  # --- 選択バイアスの可視化 ---
  geom_vline(xintercept = selection_threshold, linetype = "dashed", color = "black") +
  geom_hline(yintercept = selection_threshold, linetype = "dashed", color = "black") +
  annotate("text", x = 30, y = 30, label = "除外された領域", color = "black", size = 4) +

  # --- 凡例とラベルの設定 ---
  scale_color_manual(
    name = "回帰直線",
    values = c("全体集団" = "darkgreen", "選択された集団" = "red"), # 色を指定
    labels = c(
      paste("全体 (相関:", round(cor_population, 2), ")"),
      paste("選択後 (相関:", round(cor_selected, 2), ")")
    ) # 凡例に相関係数を表示
  ) +
  labs(
    title = "バークソンのパラドックス: 回帰直線による比較",
    subtitle = "選択バイアスにより、水平な回帰直線（無相関）が右肩下がりに変化する",
    x = "才能スコア",
    y = "人柄スコア"
  ) +
  theme_minimal() +
  theme(legend.position = "bottom") # 凡例をプロットの下に配置

# プロットを表示
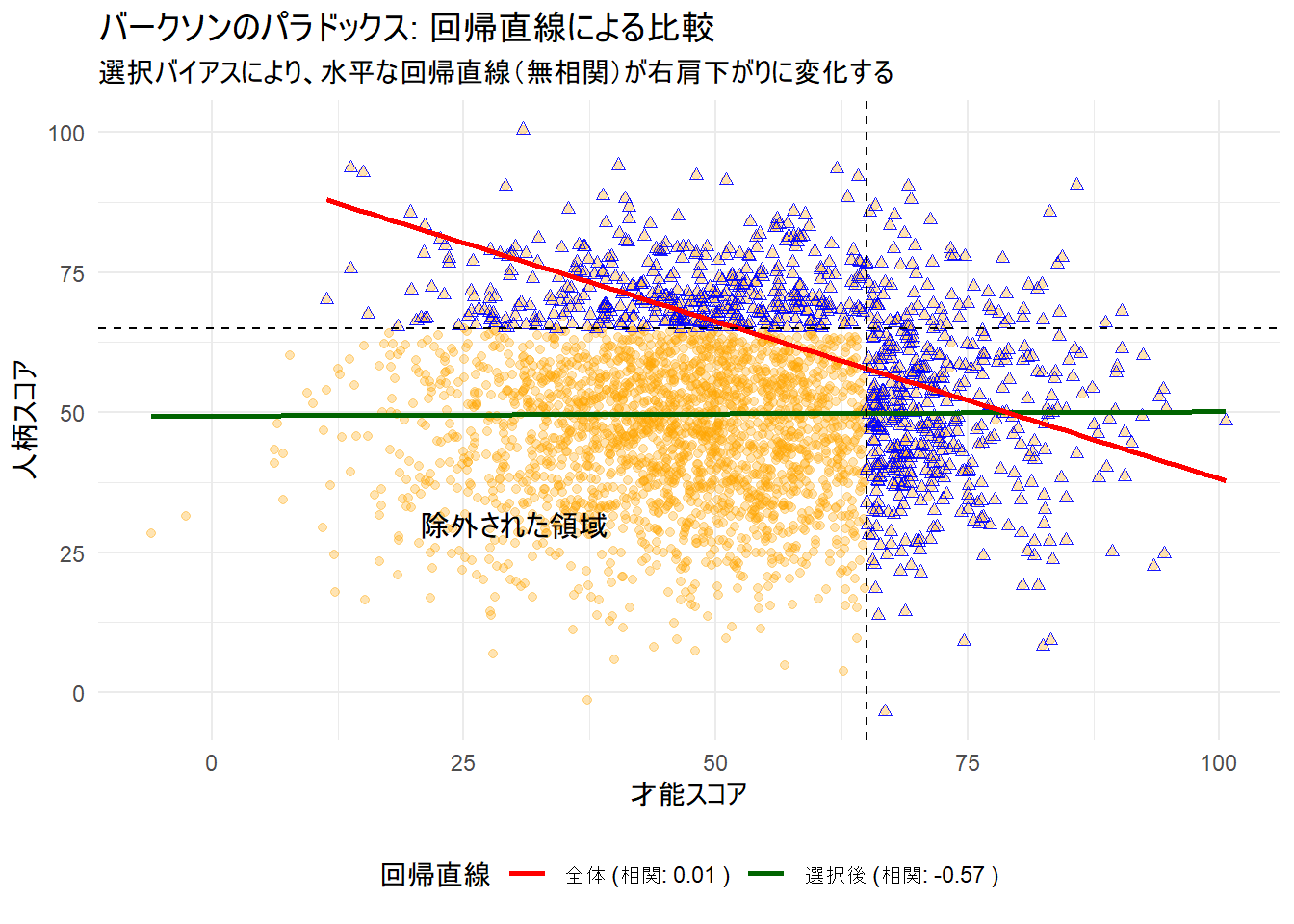
print(p_combined_reg)

シミュレーション結果の解説

上記のコードを実行すると、散布図に2本の回帰直線が追加されたグラフが生成されます。

緑色の直線（全体集団の回帰直線）:
- オレンジ色の点（全体集団）の傾向を示しています(除外された領域外では青色の点が重なっています)。
- この直線はほぼ水平です。これは「才能」スコアが高くても低くても、「人柄」スコアの平均的な値は変わらない、つまり2つの変数に相関がないことを明確に示しています。凡例にも相関係数が約0.01と表示されています。
赤色の直線（選択された集団の回帰直線）:
- 青色の点（選択された集団）の傾向を示しています。
- この直線は明確な右肩下がりになっています。これは、この集団の中では「才能」スコアが高いほど「人柄」スコアが低い傾向にある、という見かけ上の負の相関があることを示しています。凡例の相関係数も約-0.57と、負の相関です。