Rで意思決定:サンクトペテルブルクのパラドックス

ゲームのルール

このパラドックスで提示されるゲームのルールは非常にシンプルです。

1. 参加者はまず、参加費を支払います。
2. 主催者は公正なコイン（表と裏が出る確率がそれぞれ1/2）を投げ始めます。
3. コインを投げ続け、初めて表（Head）が出た時点でゲームは終了します。
4. 賞金は、初めて表が出るまでにコインを投げた回数 n によって決まります。賞金額は 2ⁿ ドルです。

具体的には、

• 1回目で表が出たら、賞金は 2¹ = 2ドル
• 2回目で初めて表が出たら（裏→表）、賞金は 2² = 4ドル
• 3回目で初めて表が出たら（裏→裏→表）、賞金は 2³ = 8ドル
• …
• n回目で初めて表が出たら、賞金は 2ⁿ ドル

となります。

何がパラドックスなのか？

このゲームの参加費はいくらが妥当でしょうか？経済学の基本的な考え方では、ゲームの「期待値」がその価値とされます。期待値を計算してみましょう。

• 1回目で表が出る確率: 1/2。賞金は2ドル。 → 期待値への寄与: (1/2) * 2 = 1ドル
• 2回目で表が出る確率: 1/4。賞金は4ドル。 → 期待値への寄与: (1/4) * 4 = 1ドル
• 3回目で表が出る確率: 1/8。賞金は8ドル。 → 期待値への寄与: (1/8) * 8 = 1ドル
• n回目で表が出る確率: (1/2)ⁿ。賞金は2ⁿドル。 → 期待値への寄与: (1/2)ⁿ * 2ⁿ = 1ドル

このゲームの期待値 (E) は、これらの合計になります。

E = 1 + 1 + 1 + 1 + … = ∞ (無限大)

期待値が無限大ということは、計算上はこのゲームにどんなに高額な参加費を払ってでも参加すべき、ということになります。

しかし、私たちの直感ではどうでしょうか？ ほとんどのゲームはすぐに終わってしまいます。

• 50%の確率で、賞金はたったの2ドルです。
• 75%の確率で、賞金は4ドル以下です。
• 93.75%の確率で、賞金は16ドル以下です。

このように、ほとんどの場合は少額の賞金しか得られないため、多くの人はこのゲームの参加費として20ドルや30ドルでさえも高く感じてしまいます。

この「理論上の期待値（無限大）と、人々が感じる妥当な参加費（少額）との間の大きな隔たり」が、サンクトペテルブルクのパラドックスです。このパラドックスは、金銭の価値は金額そのものではなく、人がそれによって得られる「効用（満足度）」によって決まるという「期待効用理論」の発展につながりました。

ステップ1: 1回のゲームをシミュレートする関数を作成

まず、1回のコイントスゲームを実行し、賞金を返す関数を定義します。

# サンクトペテルブルクのゲームを1回プレイする関数
play_st_petersburg <- function() {
  n <- 1 # コインを投げた回数
  while (TRUE) {
    # 1が表(Head)、0が裏(Tail)とする
    coin_toss <- sample(c(0, 1), 1)

    if (coin_toss == 1) {
      # 表が出たらループを抜ける
      break
    } else {
      # 裏が出たら回数を増やして続ける
      n <- n + 1
    }
  }

  # 賞金 2^n を返す
  prize <- 2^n
  return(prize)
}

# 関数の動作テスト
# play_st_petersburg()

ステップ2: 多数回のシミュレーションを実行

次に、この関数を10万回実行して、各回の賞金を記録します。

# 再現性のために乱数のシードを設定
seed <- 20250818
set.seed(seed)

# シミュレーション回数を設定
num_simulations <- 100000

# replicate関数を使って指定回数だけゲームを実行し、結果をベクトルに格納
results <- replicate(num_simulations, play_st_petersburg())

ステップ3: 結果の分析と可視化

シミュレーション結果から、ほとんどのゲームは少額の賞金で終わること、つまり、大金を期待するのは現実的ではないこと(=高い参加費を払いたがらない直感的な理由)を確認します。

# 結果の要約統計量
summary(results)

     Min.   1st Qu.    Median      Mean   3rd Qu.      Max. 
     2.00      2.00      2.00     22.73      4.00 262144.00 

2. 賞金の分布をヒストグラムで確認

ほとんどのゲームが少額で終わることをヒストグラムで確認します。賞金の範囲が広すぎるため、ここでは32ドル以下の結果に絞ってプロットします。

# 賞金の分布をヒストグラムで可視化
# 非常に大きな外れ値があるため、表示範囲を限定する
hist(results[results <= 32],
  breaks = seq(0, 32, by = 2),
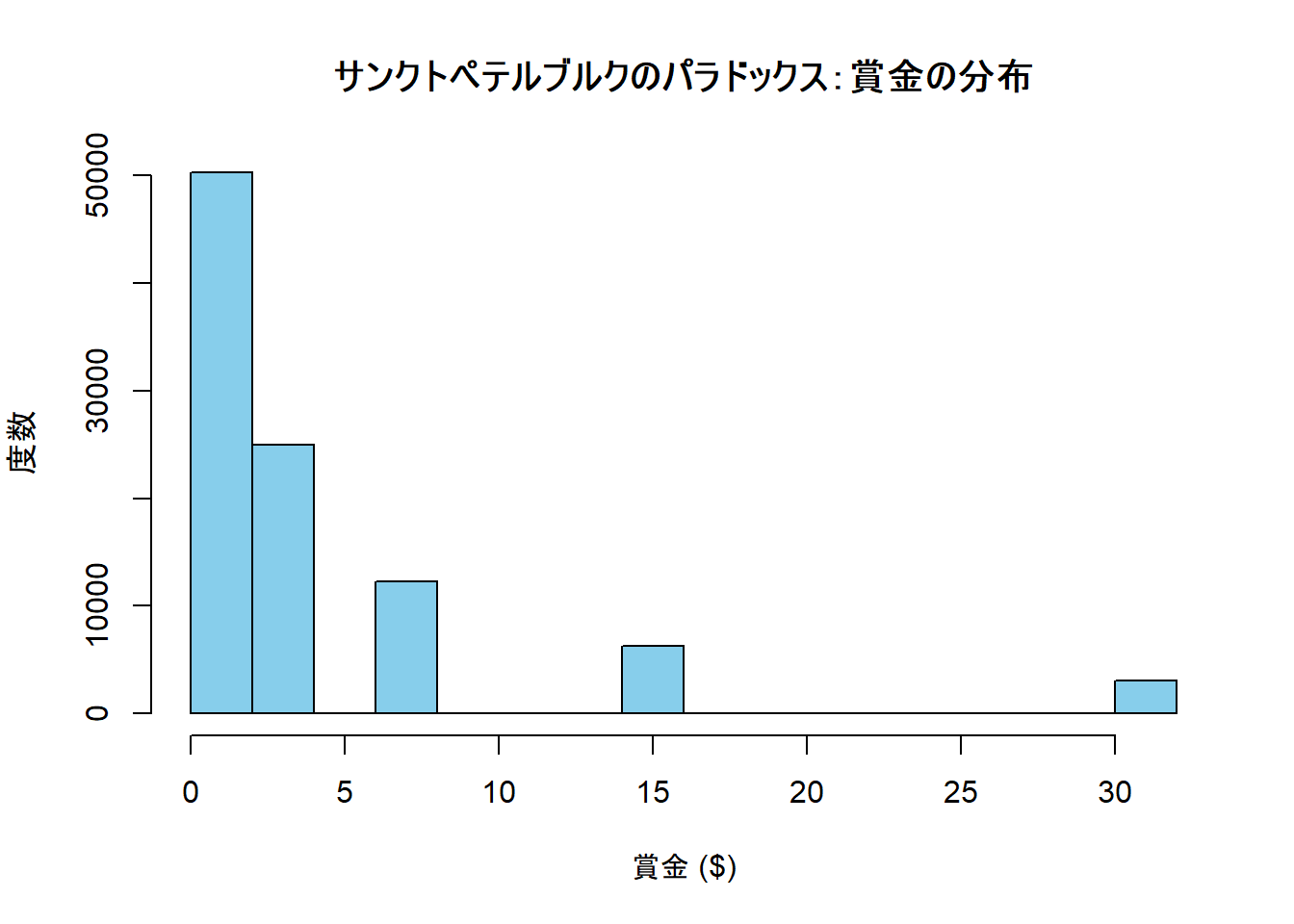
  main = "サンクトペテルブルクのパラドックス：賞金の分布",
  xlab = "賞金 ($)",
  ylab = "度数",
  col = "skyblue"
)

cat(paste0("10万回の試行中、", length(results[results <= 8]), " 回で8ドル以下。"))

10万回の試行中、87538 回で8ドル以下。

Figure 1 から、圧倒的多数のゲームが2ドル、4ドル、8ドルといった低い賞金で終了していることが分かります。

以上です。