Rで意思決定:線形計画法

概要

線形計画法（LP）は、与えられた制約の中で、ある目的を最大化または最小化するための最適な方法を見つけ出す数学的な手法です。オペレーションズ・リサーチの一分野であり、経営、生産管理、金融、物流など、限られたリソース（資源）を最も効率的に配分する問題の解決に広く利用されています。

名前の通り、扱う数式がすべて線形（一次式）であることが特徴です。これにより、問題を幾何学的に解釈したり、効率的なアルゴリズム（シンプレックス法など）で解を求めたりすることが可能になります。

線形計画問題を構成する3つの要素

線形計画問題は、以下の3つの要素で構成されます。

1. 目的関数 (Objective Function) 最大化または最小化したい対象を数式で表したものです。
   • 例：利益を最大化したい → 最大化 Z = (製品Aの利益) × (Aの生産量) + (製品Bの利益) × (Bの生産量)
2. 制約条件 (Constraints) 使用できるリソース（時間、予算、原材料、人員など）の限界や、満たすべき要件を不等式または等式で表したものです。
   • 例：原材料Xの使用量は100kgまで → (Aに使うXの量) × (Aの生産量) + (Bに使うXの量) × (Bの生産量) ≤ 100
3. 非負条件 (Non-negativity Constraints) 決定変数（生産量など）がマイナスになることは現実的にありえないため、通常はすべての変数が0以上であるという条件が加わります。
   • 例：(Aの生産量) ≥ 0, (Bの生産量) ≥ 0

具体例：工場の生産計画

ある工場が2種類の製品AとBを生産しているとします。

• 利益: 製品Aは1個あたり4千円、製品Bは1個あたり5千円の利益。
• 原材料:
  • 製品Aを1個作るのに、原材料Pが1kg、原材料Qが2kg必要。
  • 製品Bを1個作るのに、原材料Pが3kg、原材料Qが1kg必要。
• 在庫: 原材料Pの在庫は90kg、原材料Qの在庫は80kgまでしか使えない。

このとき、総利益を最大化するには、製品AとBをそれぞれ何個ずつ生産すればよいでしょうか？

これを線形計画問題として定式化すると以下のようになります。

• 決定変数:
  • 製品Aの生産量を x 個
  • 製品Bの生産量を y 個
• 目的関数（利益の最大化）:
  • 最大化 Z = 4x + 5y
• 制約条件:
  • 原材料P: 1x + 3y ≤ 90
  • 原材料Q: 2x + 1y ≤ 80
• 非負条件:
  • x ≥ 0, y ≥ 0

線形計画法は、この連立不等式が満たす領域（実行可能領域）の中で、目的関数 Z の値が最も大きくなる点 (x, y) を見つけ出す手法です。2変数の場合はグラフを描画して解くことも可能で、解は実行可能領域の頂点のいずれかに存在することが知られています。

シミュレーションの準備

まず、lpSolveパッケージを読み込みます。

# パッケージを読み込む
library(lpSolve)

ステップ1：問題の定式化とRへの入力

先ほどの「工場の生産計画」の例をlpSolveパッケージのlp()関数で解いてみましょう。

lp()関数は、以下の主要な引数を取ります。

• direction: “max” (最大化) または “min” (最小化) を指定。
• objective.in: 目的関数の係数をベクトルで指定。
• const.mat: 制約条件の左辺の係数を行列で指定。
• const.dir: 制約条件の不等号（<=, >=, ==）をベクトルで指定。
• const.rhs: 制約条件の右辺の値をベクトルで指定。

# 1. 目的関数の係数ベクトル (Z = 4x + 5y)
# 変数の順序は (x, y) とする
objective_coeffs <- c(4, 5)

# 2. 制約条件の係数行列
# 1行目: 原材料Pの制約 (1x + 3y)
# 2行目: 原材料Qの制約 (2x + 1y)
constraints_matrix <- matrix(c(
  1, 3,
  2, 1
), nrow = 2, byrow = TRUE)

# 3. 制約条件の不等号
constraints_dir <- c("<=", "<=")

# 4. 制約条件の右辺の値
constraints_rhs <- c(90, 80)

# 5. LP問題を解く
solution <- lp(
  direction = "max",
  objective.in = objective_coeffs,
  const.mat = constraints_matrix,
  const.dir = constraints_dir,
  const.rhs = constraints_rhs,
  all.int = TRUE # 生産量は整数であるため、整数計画問題として解く
)

• all.int = TRUE は、すべての変数が整数でなければならないという制約を追加します。今回のように個数を扱う問題では TRUE とします。

ステップ2：結果の確認と解釈

lp()関数が返すオブジェクトには、解に関する情報が含まれています。

# --- 結果の表示 ---

# 計算が成功したか確認 (0は成功)
if (solution$status == 0) {
  # 最適な目的関数の値 (最大利益)
  max_profit <- solution$objval

  # 最適な決定変数の値 (最適な生産量)
  optimal_production <- solution$solution

  cat("線形計画法のシミュレーション結果:\n")
  cat("----------------------------------\n")
  cat(sprintf("製品Aの最適な生産量 (x): %d 個\n", optimal_production[1]))
  cat(sprintf("製品Bの最適な生産量 (y): %d 個\n", optimal_production[2]))
  cat("----------------------------------\n")
  cat(sprintf("達成される最大利益 (Z): %d 千円\n", max_profit))
} else {
  cat("最適解を見つけることができませんでした。ステータスコード:", solution$status, "\n")
}

線形計画法のシミュレーション結果:
----------------------------------
製品Aの最適な生産量 (x): 30 個
製品Bの最適な生産量 (y): 20 個
----------------------------------
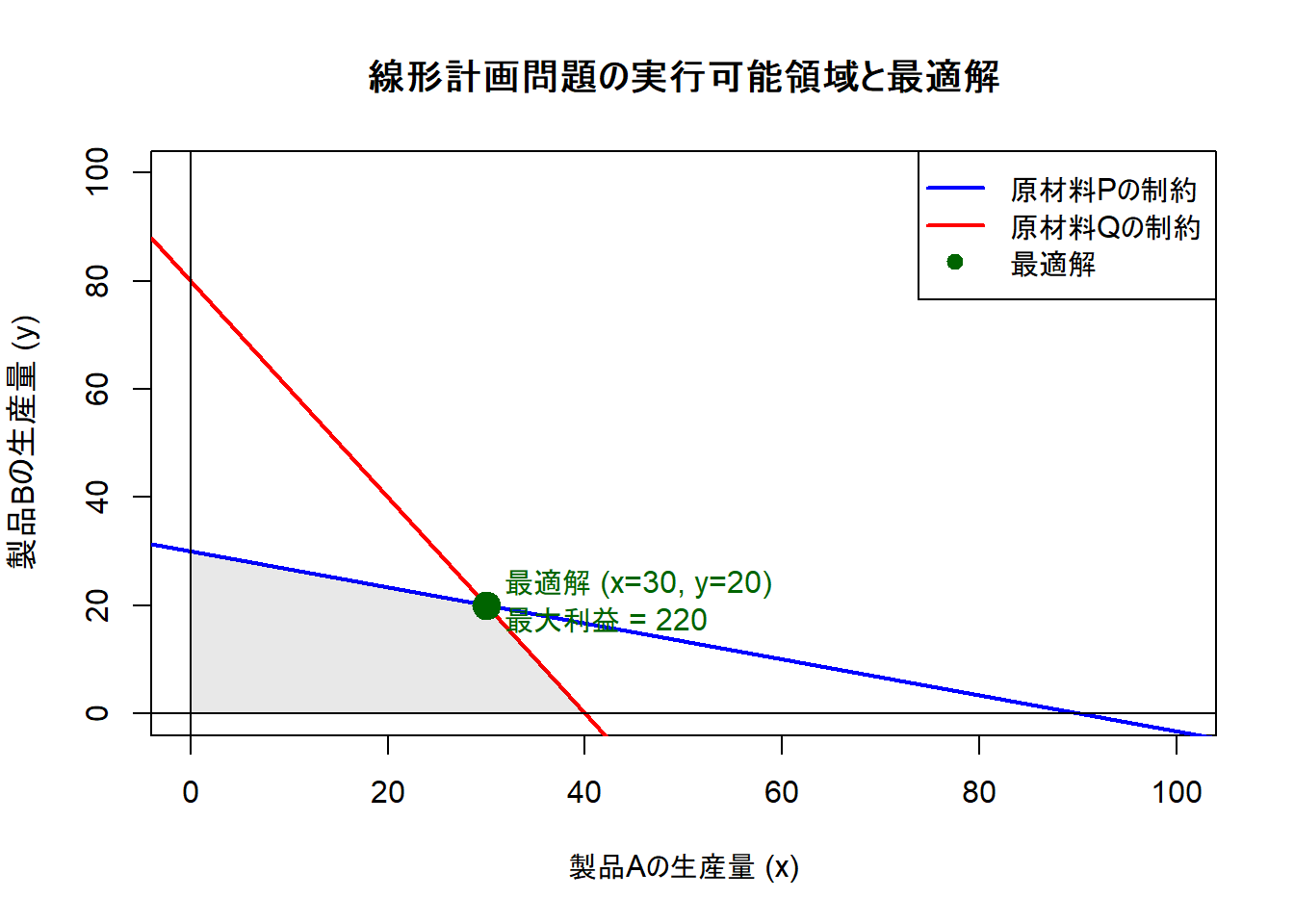
達成される最大利益 (Z): 220 千円

この結果から、製品Aを30個、製品Bを20個生産したときに、制約条件を守りつつ総利益が最大の220千円になることが分かりました。

ステップ3：結果の可視化（2変数の場合）

この問題は2変数（x, y）ですので、グラフで解を視覚的に理解することができます。

# グラフ描画エリアの設定
plot(NULL,
  xlim = c(0, 100), ylim = c(0, 100),
  xlab = "製品Aの生産量 (x)", ylab = "製品Bの生産量 (y)",
  main = "線形計画問題の実行可能領域と最適解"
)

# 制約条件の境界線を描画
# 1. 1x + 3y = 90  => y = (90 - x) / 3
abline(a = 90 / 3, b = -1 / 3, col = "blue", lwd = 2)
# 2. 2x + 1y = 80  => y = 80 - 2x
abline(a = 80, b = -2, col = "red", lwd = 2)
# 3. x=0, y=0 (軸)
abline(h = 0, v = 0)

# 実行可能領域をポリゴンで塗りつぶす
# 領域の頂点を計算
p1 <- c(0, 0)
p2 <- c(40, 0) # 2x+y=80 と y=0 の交点
# 1x+3y=90 と 2x+y=80 の交点
A <- matrix(c(1, 3, 2, 1), 2, 2, byrow = T)
b <- c(90, 80)
p3 <- solve(A, b)
p4 <- c(0, 30) # 1x+3y=90 と x=0 の交点

# 頂点の座標をまとめる
feasible_region <- data.frame(
  x = c(p1[1], p2[1], p3[1], p4[1]),
  y = c(p1[2], p2[2], p3[2], p4[2])
)
polygon(feasible_region$x, feasible_region$y, col = rgb(0.1, 0.1, 0.1, 0.1), border = NA)

# 最適解の点をプロット
points(optimal_production[1], optimal_production[2], col = "darkgreen", pch = 19, cex = 2)
text(optimal_production[1], optimal_production[2],
  labels = sprintf(
    "最適解 (x=%d, y=%d)\n最大利益 = %d",
    optimal_production[1], optimal_production[2], max_profit
  ),
  pos = 4, col = "darkgreen"
)

# 凡例を追加
legend("topright",
  legend = c("原材料Pの制約", "原材料Qの制約", "最適解"),
  col = c("blue", "red", "darkgreen"), lty = c(1, 1, NA), pch = c(NA, NA, 19), lwd = 2
)

Figure 1 により、青色と赤色の線で囲まれたグレーの領域（実行可能領域）の中で、緑色の点が目的関数（総利益）を最大化する点であることが視覚的に確認できます。

以上です。