Rで 意思決定:階層分析法 を試みます。
本ポストはこちらの続きです。

1. 階層分析法(AHP)とは
概要
階層分析法(AHP)は、1970年代にトーマス・L・サーティによって提唱された、複雑な問題における意思決定を支援するための手法です。
人間が直面する問題には、「コスト」、「品質」、「デザイン」のように、複数の評価基準が絡み合い、単純に比較できないものが多くあります。AHPは、このような複雑な問題を階層構造に分解し、各要素を一対比較することで、それぞれの重要度(ウェイト)を数値化します。最終的に、それらを統合して最も合理的な選択肢(代替案)を導き出すことを目標とします。
個人の主観や経験といった定性的な判断を、定量的・論理的に扱うことをできるのが大きな特徴です。
AHPの手順
AHPは、主に以下のステップで進められます。
ステップ1:問題の階層化
意思決定問題を、以下の3つの階層に分解・整理します。
- 最終目標 (Goal): 達成したい最終的な目的(例:最適なスマートフォンの選択)
- 評価基準 (Criteria): 最終目標を達成するために考慮すべき評価項目(例:バッテリー、デザイン、価格、カメラ性能)
- 代替案 (Alternatives): 選択肢となる具体的な候補(例:スマホA、スマホB、スマホC)
図にすると、以下のようになります。
ステップ2:一対比較
各階層の要素について、「どちらが、どれくらい重要か(優れているか)」をペアで比較していきます。この比較には、以下の9段階の尺度(サーティの尺度)がよく用いられます。
| 評価値 | 意味 |
|---|---|
| 1 | 等しい重要度 |
| 3 | やや重要 |
| 5 | かなり重要 |
| 7 | 非常に重要 |
| 9 | 絶対的に重要 |
| 2,4,6,8 | 上記の中間の評価 |
例えば、「価格」と「カメラ性能」を比較して、「価格の方がカメラ性能よりかなり重要」と判断した場合、「価格」の評価値は「5」となります。この結果を「一対比較行列」という表にまとめていきます。
ステップ3:ウェイト(重要度)の算出
ステップ2で作成した一対比較行列から、各要素のウェイト(重要度や優先度を表す数値)を計算します。具体的には、行列の最大固有値とそれに対応する固有ベクトルを求めることでウェイトを算出します(固有値法)。
ステップ4:整合性の検証
一対比較では、「AはBより重要、BはCより重要、なのにCはAより重要」といった矛盾した回答をしてしまう可能性があります。このような回答の矛盾の度合いをチェックするのが「整合性の検証」です。
そこで、整合性指数(CI: Consistency Index)と整合性比率(CR: Consistency Ratio)という指標を計算し、CRが一定の基準値(一般的に0.1)以下であれば、その回答は整合性が取れていると判断します。基準値を超えた場合は、一対比較をやり直すことが推奨されます。
ステップ5:総合評価
最後に、算出した「評価基準のウェイト」と「各評価基準における代替案のウェイト」を掛け合わせ、代替案ごとの総合スコアを計算します。このスコアが最も高い代替案が、最も合理的な選択肢となります。
2. R言語による階層分析法(AHP)のシミュレーション
ここでは、「新しいスマートフォンの選択」というテーマでAHPのシミュレーションを行います。
- 最終目標: 自分に最適なスマートフォンを選ぶ
- 評価基準: 価格、カメラ性能、バッテリー、デザイン
- 代替案: スマホA、スマホB、スマホC
ステップ1 & 2:一対比較行列の作成
まず、評価基準同士を一対比較します。ここでは、以下のような判断をしたと仮定します。
- 価格は、カメラ性能より「かなり重要」(5)
- 価格は、バッテリーより「やや重要」(3)
- カメラ性能は、デザインより「非常に重要」(7)
- …など
この結果をmatrixで表現します。対角成分は常に1で、A[j, i] = 1 / A[i, j]の関係になります。
# 評価基準の一対比較行列
# 行/列の順: 価格, カメラ, バッテリー, デザイン
criteria_matrix <- matrix(c(
1, 5, 3, 7,
1 / 5, 1, 1 / 3, 3,
1 / 3, 3, 1, 5,
1 / 7, 1 / 3, 1 / 5, 1
), nrow = 4, byrow = TRUE)
# 行名と列名を設定して分かりやすくする
dimnames(criteria_matrix) <- list(
c("価格", "カメラ", "バッテリー", "デザイン"),
c("価格", "カメラ", "バッテリー", "デザイン")
)
cat("評価基準の一対比較行列:\n")
print(criteria_matrix)評価基準の一対比較行列:
価格 カメラ バッテリー デザイン
価格 1.0000000 5.0000000 3.0000000 7
カメラ 0.2000000 1.0000000 0.3333333 3
バッテリー 0.3333333 3.0000000 1.0000000 5
デザイン 0.1428571 0.3333333 0.2000000 1次に、各評価基準について、代替案(スマホA, B, C)をそれぞれ一対比較します。
# --- 代替案の一対比較行列 ---
# 行/列の順: スマホA, スマホB, スマホC
# 1. 「価格」の観点での比較 (価格が安いほど良い)
# 例: スマホAはBより「かなり安い」(5)、CはAより「やや安い」(1/3)
price_matrix <- matrix(c(
1, 5, 1 / 3,
1 / 5, 1, 1 / 7,
3, 7, 1
), nrow = 3, byrow = TRUE)
dimnames(price_matrix) <- list(c("スマホA", "スマホB", "スマホC"), c("スマホA", "スマホB", "スマホC"))
# 2. 「カメラ性能」の観点での比較
# 例: スマホBはAより「やや優れている」(3)、BはCと「同等」(1)
camera_matrix <- matrix(c(
1, 1 / 3, 3,
3, 1, 5,
1 / 3, 1 / 5, 1
), nrow = 3, byrow = TRUE)
dimnames(camera_matrix) <- list(c("スマホA", "スマホB", "スマホC"), c("スマホA", "スマホB", "スマホC"))
# 3. 「バッテリー」の観点での比較
# 例: スマホCはA、Bより「非常に優れている」(7)
battery_matrix <- matrix(c(
1, 3, 1 / 7,
1 / 3, 1, 1 / 9,
7, 9, 1
), nrow = 3, byrow = TRUE)
dimnames(battery_matrix) <- list(c("スマホA", "スマホB", "スマホC"), c("スマホA", "スマホB", "スマホC"))
# 4. 「デザイン」の観点での比較
# 例: スマホAとBは同等(1)、AはCより「かなり良い」(5)
design_matrix <- matrix(c(
1, 1, 5,
1, 1, 5,
1 / 5, 1 / 5, 1
), nrow = 3, byrow = TRUE)
dimnames(design_matrix) <- list(c("スマホA", "スマホB", "スマホC"), c("スマホA", "スマホB", "スマホC"))
cat("「価格」に関する代替案の比較行列:\n")
print(price_matrix)「価格」に関する代替案の比較行列:
スマホA スマホB スマホC
スマホA 1.0 5 0.3333333
スマホB 0.2 1 0.1428571
スマホC 3.0 7 1.0000000ステップ3:ウェイト(重要度)の算出
固有値法を用いて、各行列からウェイトを計算する関数を定義します。
# ウェイトを計算する関数 (固有値法)
calculate_weights <- function(mat) {
# 固有値と固有ベクトルを計算
eig <- eigen(mat)
# 最大固有値に対応する固有ベクトルを取得 (実数部のみ)
# which.max(Re(eig$values)) で最大固有値のインデックスを探す
max_eigen_vec <- Re(eig$vectors[, which.max(Re(eig$values))])
# 固有ベクトルを正規化(合計が1になるように)してウェイトとする
weights <- max_eigen_vec / sum(max_eigen_vec)
# 最大固有値も返す
return(list(weights = weights, max_eigen_value = max(Re(eig$values))))
}
# 各行列のウェイトを計算
criteria_result <- calculate_weights(criteria_matrix)
weights_criteria <- criteria_result$weights
price_weights <- calculate_weights(price_matrix)$weights
camera_weights <- calculate_weights(camera_matrix)$weights
battery_weights <- calculate_weights(battery_matrix)$weights
design_weights <- calculate_weights(design_matrix)$weights
cat("評価基準のウェイト:\n")
# 分かりやすいように名前を付ける
names(weights_criteria) <- rownames(criteria_matrix)
print(weights_criteria)評価基準のウェイト:
価格 カメラ バッテリー デザイン
0.56500905 0.11750425 0.26220121 0.05528549 ステップ4:整合性の検証
CR(整合性比率)を計算して、回答の矛盾をチェックする関数を定義します。
# RI (Random Index) 表:行列のサイズに応じたランダムな行列の平均的な整合性指数
# サイズ n = 1, 2, ..., 10
RI_table <- c(0, 0, 0.58, 0.90, 1.12, 1.24, 1.32, 1.41, 1.45, 1.49)
# 整合性を検証する関数
check_consistency <- function(mat, max_eigen_value) {
n <- nrow(mat)
# CI (整合性指数) の計算
CI <- (max_eigen_value - n) / (n - 1)
# RI の取得
RI <- RI_table[n]
# CR (整合性比率) の計算
if (RI > 0) {
CR <- CI / RI
} else {
CR <- 0 # n=1,2 の場合は矛盾が生じないので0
}
cat(sprintf("行列サイズ: %d\n", n))
cat(sprintf("最大固有値 (λmax): %.4f\n", max_eigen_value))
cat(sprintf("CI: %.4f\n", CI))
cat(sprintf("CR: %.4f\n", CR))
if (CR < 0.1) {
cat("結果: 整合性は十分に保たれています。\n\n")
} else {
cat("結果: 整合性が低いため、一対比較の見直しを推奨します。\n\n")
}
}
# 評価基準行列の整合性を検証
cat("--- 評価基準行列の整合性チェック ---\n")
check_consistency(criteria_matrix, criteria_result$max_eigen_value)--- 評価基準行列の整合性チェック ---
行列サイズ: 4
最大固有値 (λmax): 4.1170
CI: 0.0390
CR: 0.0433
結果: 整合性は十分に保たれています。このシミュレーションの例では、CRが0.1を下回るため、回答には十分な整合性があると判断できます。
ステップ5:総合評価
算出した各ウェイトを統合し、最終的なスコアを計算します。
# 代替案ごとのウェイトを一つの行列にまとめる
# 列が代替案(スマホA, B, C)、行が評価基準
alternative_weights_matrix <- cbind(
price_weights,
camera_weights,
battery_weights,
design_weights
)
colnames(alternative_weights_matrix) <- c("価格", "カメラ", "バッテリー", "デザイン")
rownames(alternative_weights_matrix) <- c("スマホA", "スマホB", "スマホC")
cat("各評価基準における代替案のウェイト行列:\n")
print(t(alternative_weights_matrix))
# 総合スコアの計算 (行列の積)
# (評価基準のウェイトベクトル) %*% (代替案のウェイト行列)
final_scores <- alternative_weights_matrix %*% weights_criteria
# 総合スコアの表示
cat("\n--- 総合評価スコア ---\n")
print(final_scores)
# 最適な代替案の特定
# which.maxはベクトルのインデックスを返すため、行列の行名から名前を取得
best_alternative <- rownames(final_scores)[which.max(final_scores)]
cat(sprintf("\n最適な選択肢は「%s」です。\n", best_alternative))
# --- 可視化コード ---
# final_scoresを行列からベクトルに変換してbarplotに渡す
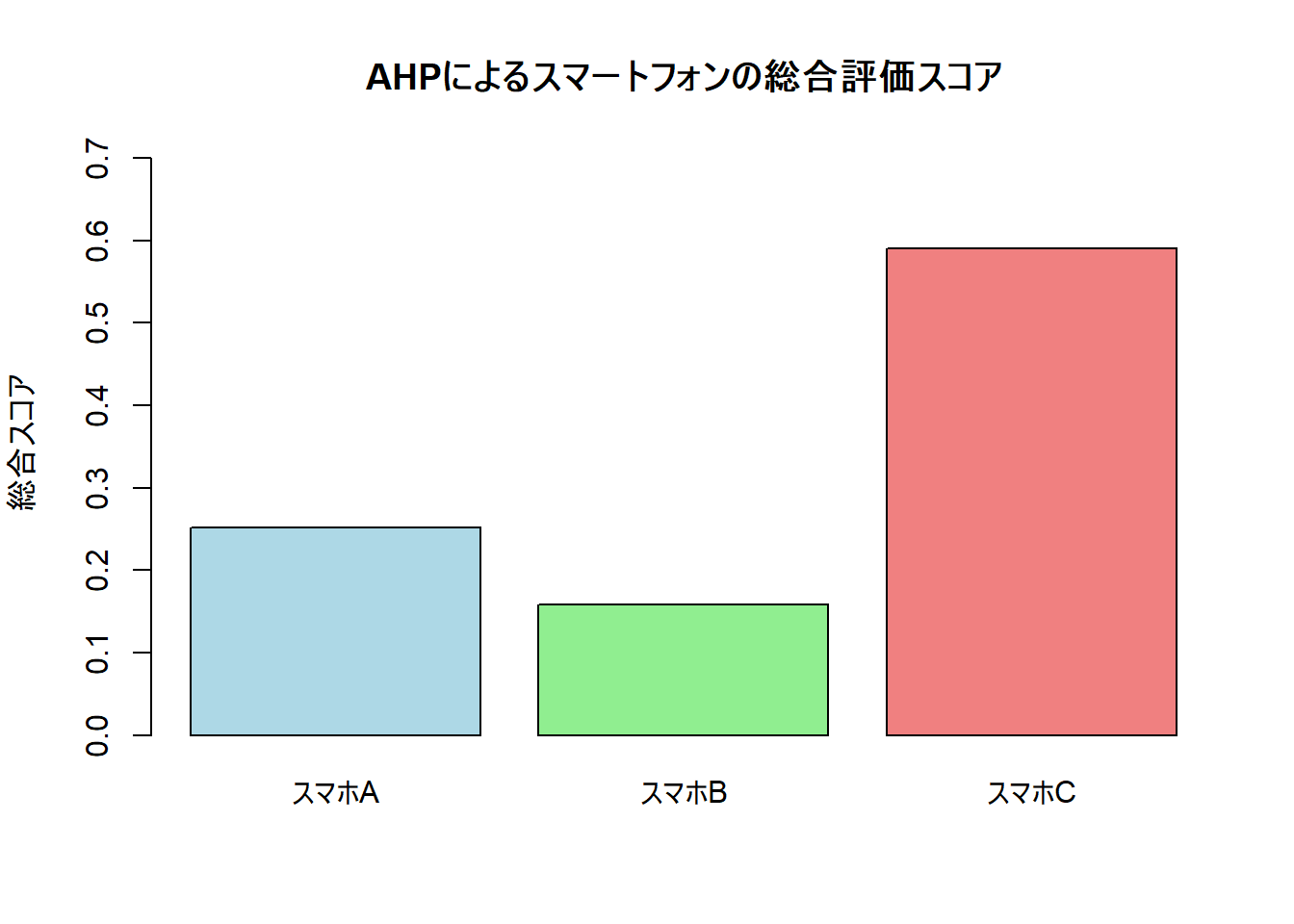
barplot(final_scores[, 1],
main = "AHPによるスマートフォンの総合評価スコア",
ylab = "総合スコア",
names.arg = rownames(final_scores), # 各棒のラベルを明示的に指定
col = c("lightblue", "lightgreen", "lightcoral"),
ylim = c(0, max(final_scores) * 1.2)
)各評価基準における代替案のウェイト行列:
スマホA スマホB スマホC
価格 0.2789546 0.07192743 0.64911800
カメラ 0.2582850 0.63698557 0.10472943
バッテリー 0.1488151 0.06579374 0.78539119
デザイン 0.4545455 0.45454545 0.09090909
--- 総合評価スコア ---
[,1]
スマホA 0.2521107
スマホB 0.1578691
スマホC 0.5900202
最適な選択肢は「スマホC」です。3. シミュレーション結果の解釈
今回のシミュレーション結果によれば、総合スコアが最も高い「スマホC」が、設定した評価基準と個人の判断に基づいた最適なスマートフォンであると結論付けられます。
その理由を詳しく見てみましょう。
まず、評価基準自体の重要度(ウェイト)は、「価格」が 約56.5% と最も高く、次いで「バッテリー」(約26.2%)が高いという設定でした(weights_criteria`)。
各評価基準における代替案のウェイトを見ると、以下のことが分かります。
- 価格: スマホC (0.649) > スマホA (0.278) > スマホB (0.071)
- バッテリー: スマホC (0.785) > スマホA (0.148) > スマホB (0.065)
- カメラ: スマホB (0.636) > スマホA (0.258) > スマホC (0.104)
- デザイン: スマホA (0.454) ≒ スマホB (0.454) > スマホC (0.090)
つまり、「スマホC」は、最も重要視していた「価格」と、2番目に重要視していた「バッテリー」の両方で、他の選択肢よりも高い評価を得ています。
一方で、「カメラ」や「デザイン」の評価は3つの代替案の中で最も低くなっていますが、AHPではこれらの評価基準の重要度が比較的低く設定されていたため、総合スコアへのマイナスの影響は限定的でした。
結論として、AHPは、個人の「何を重視するか」という価値判断(評価基準のウェイト)を反映し、その上で各選択肢の長所と短所を定量的に評価・統合します。
今回のケースでは、「価格とバッテリーを最優先する」という意思決定者の判断に基づき、それらの点で最も優れた「スマホC」が最適な選択肢として導き出されたと言えます。
以上です。