Rで意思決定:非線形計画法

Rで 意思決定:非線形計画法 を試みます。

本ポストはこちらの続きです。

Rで意思決定:線形計画法を試みます。本ポストはこちらの続きです。1. 線形計画法（LP）の解説概要線形計画法（LP）は、与えられた制約の中で、ある目的を最大化または最小化するための最適な方法を見つけ出す数学的な手法です。オペレーションズ...

1. 非線形計画法（NLP）の解説

概要

非線形計画法（NLP）は、線形計画法（LP）をより一般化したもので、目的関数または制約条件の少なくとも一つが非線形（二次関数、分数関数、指数関数など）の数式で表される最適化問題です。

現実世界の問題は、必ずしも直線的な関係だけでモデル化できるとは限りません。例えば、投資のリスク（分散）は投資額の二乗に比例したり、生産量が増えると効率が上がってコストの伸びが鈍化したり（またはその逆）することがあります。こうした複雑な関係性を扱うことができるのが非線形計画法です。

線形計画法（LP）との主な違いと難しさ

項目	線形計画法 (LP)	非線形計画法 (NLP)
数式	目的関数・制約条件がすべて線形（一次式）	目的関数・制約条件のいずれかが非線形
実行可能領域	凸多角形（角ばった領域）	曲線を含む領域（丸みを帯びた領域）
最適解の場所	必ず領域の頂点に存在する	領域の頂点、辺の上、あるいは内部のどこにでも存在しうる
解の性質	最適解はただ一つ（大域的最適解）	局所的最適解と大域的最適解が存在しうる

最も大きな違いは「局所的最適解」の存在です。これは「その近傍では最適だが、領域全体で見ると最適ではない解」のことです。山登りに例えると、ある丘の頂上（局所的最適解）にたどり着いても、隣にはもっと高い山の山頂（大域的最適解）があるかもしれません。アルゴリズムによっては、この局所最適解に陥ってしまい、真の最適解を見つけられないことがあります。

具体例：ポートフォリオ最適化

金融工学における古典的な問題です。

目的: 複数の金融資産（株、債券など）に投資する際、投資全体のリスク（分散）を最小化したい。
制約:
- 期待されるリターン（収益率）は、ある目標値（例: 5%）以上でなければならない。
- 投資額の合計は、総資産額と一致しなければならない。

この問題では、リスク（分散）が各資産への投資額の二次関数で表されるため、非線形計画問題となります。

2. R言語による非線形計画法（NLP）のシミュレーション

ここでは、ある点からの距離を最小化する、という分かりやすい例でシミュレーションを行います。

問題設定

点 P(10, 5) があるとします。以下の制約条件を満たす領域内で、点Pに最も近い点 (x, y) を見つけてください。（※距離を最小化する代わりに、計算が簡単な距離の二乗を最小化します。結果は同じです）

目的関数（距離の二乗の最小化）:
- 最小化 f(x, y) = (x - 10)^2 + (y - 5)^2 ← 二次式なので非線形
制約条件:
1. x + y ≤ 10
2. x ≤ 8
境界条件（非負条件）:
- x ≥ 0, y ≥ 0

シミュレーションの準備

# パッケージを読み込む
library(nloptr)

ステップ1：問題の定式化とRへの入力

nloptrでは、目的関数と制約条件をRのfunctionとして定義します。

# 1. 目的関数 f(x)
# xはベクトルで、x[1]がx座標、x[2]がy座標に対応
eval_f <- function(x) {
  return((x[1] - 10)^2 + (x[2] - 5)^2)
}

# 2. 目的関数の勾配
# 勾配は、各変数で偏微分したもの
eval_grad_f <- function(x) {
  return(c(2 * (x[1] - 10), 2 * (x[2] - 5)))
}

# 3. 制約条件 g(x) <= 0
# nloptrは「<= 0」の形式で制約を定義する必要がある
eval_g <- function(x) {
  # 制約1: x + y <= 10  =>  x + y - 10 <= 0
  constraint1 <- x[1] + x[2] - 10
  # 制約2: x <= 8       =>  x - 8 <= 0
  constraint2 <- x[1] - 8

  return(c(constraint1, constraint2))
}

# 4. 制約条件のヤコビアン（勾配行列）
eval_jac_g <- function(x) {
  return(rbind(c(1, 1), c(1, 0)))
}

ステップ2：ソルバーの実行

nloptr()関数に必要な情報を渡して、最適化を実行します。

# 初期値（計算の出発点）
x0 <- c(1, 1)

# 境界条件 (x >= 0, y >= 0)
lb <- c(0, 0) # lower bound
ub <- c(Inf, Inf) # upper bound

# ソルバーの実行
solution <- nloptr(
  x0 = x0,
  eval_f = eval_f,
  eval_grad_f = eval_grad_f,
  eval_g_ineq = eval_g,
  eval_jac_g_ineq = eval_jac_g,
  lb = lb,
  ub = ub,
  opts = list("algorithm" = "NLOPT_LD_SLSQP", "xtol_rel" = 1.0e-8)
)

ステップ3：結果の確認と解釈

# --- 結果の表示 ---
optimal_point <- solution$solution
min_value <- solution$objective

cat("非線形計画法のシミュレーション結果:\n")
cat("----------------------------------\n")
cat(sprintf("点P(10,5)に最も近い点 (x, y) は (%.4f, %.4f) です。\n", optimal_point[1], optimal_point[2]))
cat(sprintf("その時の目的関数の最小値（距離の二乗）は %.4f です。\n", min_value))
cat("メッセージ:", solution$message, "\n")

非線形計画法のシミュレーション結果:
----------------------------------
点P(10,5)に最も近い点 (x, y) は (7.5000, 2.5000) です。
その時の目的関数の最小値（距離の二乗）は 12.5000 です。
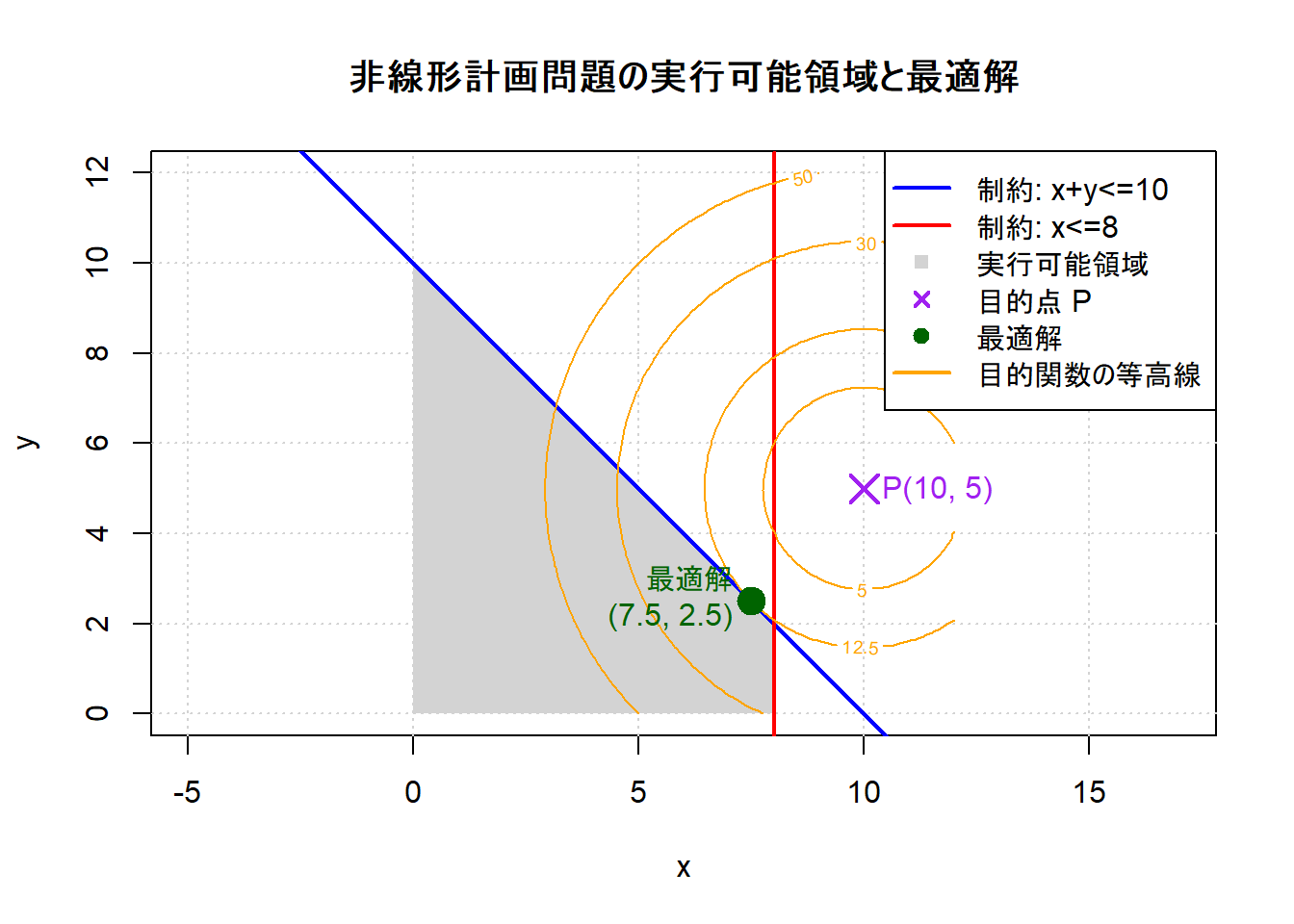
メッセージ: NLOPT_XTOL_REACHED: Optimization stopped because xtol_rel or xtol_abs (above) was reached.

この結果から、制約を満たす領域内で点 P(10, 5) に最も近い点は (7.5, 2.5) であることが分かりました。

ステップ4：結果の可視化

# グラフ描画エリアの設定
plot(NULL,
  xlim = c(0, 12), ylim = c(0, 12), asp = 1,
  xlab = "x", ylab = "y", main = "非線形計画問題の実行可能領域と最適解"
)
grid()

# 実行可能領域をポリゴンで塗りつぶす
# 領域の頂点は (0,0), (8,0), (8,2), (0,10)
feasible_region <- data.frame(
  x = c(0, 8, 8, 0),
  y = c(0, 0, 2, 10)
)
polygon(feasible_region$x, feasible_region$y, col = "lightgray", border = NA)

# 制約条件の境界線を描画
abline(a = 10, b = -1, col = "blue", lwd = 2) # x+y=10
abline(v = 8, col = "red", lwd = 2) # x=8

# 目的点 P(10,5) をプロット
points(10, 5, col = "purple", pch = 4, cex = 2, lwd = 2)
text(10, 5, labels = "P(10, 5)", pos = 4, col = "purple")

# 目的関数の等高線を描画
x_contour <- seq(0, 12, length.out = 100)
y_contour <- seq(0, 12, length.out = 100)
z_contour <- outer(x_contour, y_contour, function(x, y) (x - 10)^2 + (y - 5)^2)
contour(x_contour, y_contour, z_contour, levels = c(5, 12.5, 30, 50), add = TRUE, col = "orange")

# 最適解の点をプロット
points(optimal_point[1], optimal_point[2], col = "darkgreen", pch = 19, cex = 2)
text(optimal_point[1], optimal_point[2],
  labels = sprintf("最適解\n(%.1f, %.1f)", optimal_point[1], optimal_point[2]),
  pos = 2, col = "darkgreen"
)

# 凡例
legend("topright",
  legend = c("制約: x+y<=10", "制約: x<=8", "実行可能領域", "目的点 P", "最適解", "目的関数の等高線"),
  col = c("blue", "red", "lightgray", "purple", "darkgreen", "orange"),
  lty = c(1, 1, NA, NA, NA, 1),
  pch = c(NA, NA, 15, 4, 19, NA),
  lwd = 2,
  bg = "white"
)