Rで時系列データ因果探索:Transfer Entropy

Transfer Entropyとは

Transfer Entropy（TE）は、情報理論の概念を用いて、2つの時系列データ間の情報の流れの方向と量を測定する手法です。これにより、一方の時系列が他方の時系列に対して持つ「因果的な影響」を推定することができます。

簡単に言うと、Transfer Entropyは「時系列Yの過去の値を知ることで、時系列Xの未来の値を予測する際の不確実性が、どれだけ減少するか」を定量化したものです。

数式で表すと、YからXへのTransfer Entropy TE(Y→X) は以下のように定義されます。

TE(Y→X) = H(X_{t+1} | X_t^{(k)}) - H(X_{t+1} | X_t^{(k)}, Y_t^{(l)})

ここで、

• H(A|B) は、Bが与えられたときのAの条件付きエントロピー（不確実性）を表します。
• X_{t+1} は、時系列Xの1ステップ未来の値です。
• X_t^{(k)} は、時刻tまでのXの過去k個の値の履歴 (X_t, X_{t-1}, ..., X_{t-k+1}) です。
• Y_t^{(l)} は、時刻tまでのYの過去l個の値の履歴 (Y_t, Y_{t-1}, ..., Y_{t-l+1}) です。

この式の意味は次の通りです。

1. 第1項: H(X_{t+1} | X_t^{(k)}): Xの過去だけを使ってXの未来を予測するときの不確実性。
2. 第2項: H(X_{t+1} | X_t^{(k)}, Y_t^{(l)}): Xの過去に加えて、Yの過去も使ってXの未来を予測するときの不確実性。

もしYがXに対して影響を与えている（情報がYからXへ流れている）ならば、Yの過去の値はXの未来を予測するのに役立つはずです。その結果、第2項の不確実性は第1項より小さくなり、TE(Y→X) は正の値を取ります。逆に、YがXに影響を与えていなければ、TE(Y→X) は0に近くなります。

Transfer Entropyの主な特徴は以下の通りです。

• 非線形性の検出: 特定の関数形（線形など）を仮定しないため、線形・非線形を問わず変数間の関係を捉えることができます。
• 方向性の特定: TE(Y→X) と TE(X→Y) を別々に計算することで、情報がどちらの方向に流れているか（XがYに影響を与えているか、YがXに影響を与えているか）を区別できます。
• グレンジャー因果性の一般化: 経済学などで用いられるグレンジャー因果性は線形モデルを前提としますが、Transfer Entropyはそれを情報理論的に一般化したものと見なせます。

シミュレーションのシナリオ

シナリオ: 「人気インフルエンサーのSNS投稿は、新商品の口コミ数を増やすのか？」

ある企業が新商品を発売し、そのプロモーションのために人気インフルエンサーを起用しました。私たちは、このインフルエンサーのプロモーション活動が、実際にSNS上での商品の口コミ数にどれだけ影響を与えたかを分析したいと考えています。

• 時系列データY: インフルエンサーが、特定の商品について言及した1日あたりのSNS投稿数。
• 時系列データX: その商品の1日あたりのSNS上の口コミ（UGC: User Generated Content）数。

仮定する因果関係:

1. YからXへの影響 (Y → X): インフルエンサーが商品を宣伝する投稿をすると（Yが増加）、翌日に商品の口コミ数が非線形に増加する（Xが増加）。
   • 非線形性の詳細: 投稿に対して相乗効果で口コミが増える、という関係を想定します。これを Y の値が3乗で X に影響する、といった形でモデル化します。
2. XからYへの影響 (X → Y): 基本的には無いと仮定します。つまり、世の中の口コミ数が増えたからといって、契約に基づいているインフルエンサーの投稿数がそれに連動して変化することはない、と考えます。

このシナリオでTransfer Entropyを計算すれば、YからXへの情報の流れ、つまりTE(Y→X)のみが統計的に有意な値として検出されるはずです。

Rによるシミュレーションコード

上記のシナリオに沿って、シミュレーションを実行するRコードを以下に示します。

# 必要なパッケージの読み込み
library(RTransferEntropy)
library(ggplot2)
library(dplyr)
library(tidyr)

# 再現性のための乱数シード設定
seed <- 20250830
set.seed(seed)

# 1. シナリオに基づいた時系列データの生成

n_obs <- 200 # 観測期間（日数）

# Y: インフルエンサーの投稿数 (原因側)
# 全く投稿しない日や1投稿の日もあれば、時々複数投稿するスパイク状のデータを想定
# ポアソン分布に従う乱数で生成
y <- rpois(n_obs, lambda = 0.5)

# X: 商品の口コミ数 (結果側)
# X_t = 0.6 * X_{t-1} + 0.9 * (Y_{t-1})^3 + noise
# -> Xは自身の前日のX(口コミの持続性)と、同じく前日のY(インフルエンサーの投稿)の**3乗**に影響される
x <- numeric(n_obs)
x[1:2] <- 5 # 初期値

for (t in 3:n_obs) {
  # 1日前のyの値が3乗で効いてくる非線形の関係
  x[t] <- 0.6 * x[t - 1] + 0.9 * (y[t - 1])^3 + rnorm(1, mean = 0, sd = 1.5)
  # 口コミ数が負にならないように調整
  if (x[t] < 0) {
    x[t] <- 0
  }
}

# 生成したデータをデータフレームにまとめる
sim_data <- data.frame(
  day = 1:n_obs,
  口コミ数_X = x,
  投稿数_Y = y
)

# 2. 生成したデータの可視化

# データを描画しやすいように縦長形式に変換
plot_data <- sim_data %>%
  pivot_longer(
    cols = c("口コミ数_X", "投稿数_Y"),
    names_to = "時系列",
    values_to = "値"
  )

# ggplotでプロットを作成
g <- ggplot(plot_data, aes(x = day, y = 値, color = 時系列)) +
  geom_line(linewidth = 0.8) +
  facet_wrap(~時系列, ncol = 1, scales = "free_y") +
  labs(
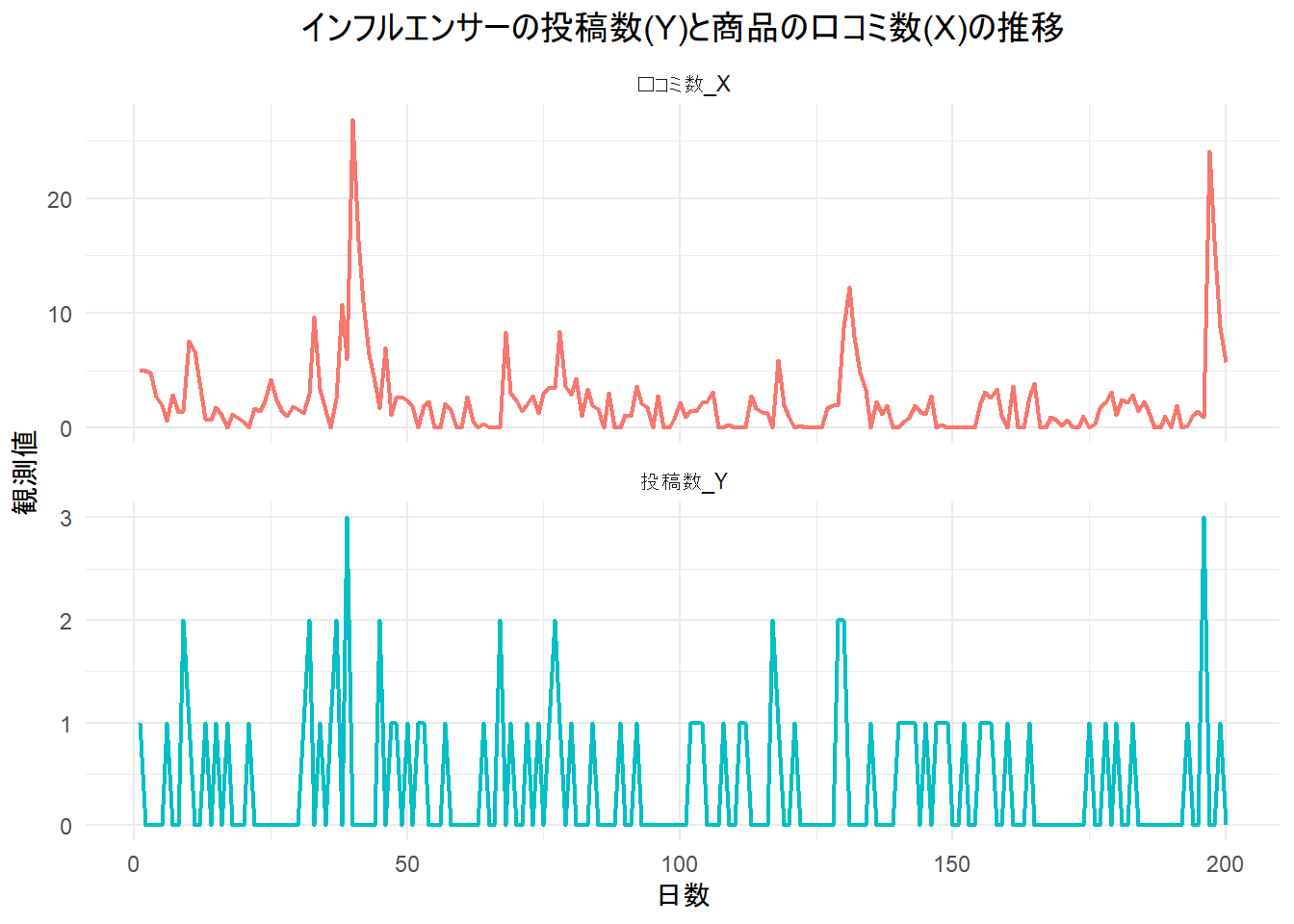
    title = "インフルエンサーの投稿数(Y)と商品の口コミ数(X)の推移",
    x = "日数",
    y = "観測値"
  ) +
  theme_minimal() +
  theme(
    legend.position = "none",
    plot.title = element_text(hjust = 0.5),
    plot.subtitle = element_text(hjust = 0.5)
  )
print(g)

• Figure 1 は、シナリオに沿った2つの時系列データ x (口コミ数) と y (投稿数) です。y はランダムなスパイク状のデータ、x は y の前日の値の3乗に影響を受ける非線形なデータとして作成されています。

# 3. Transfer Entropyの計算

# 計算を実行する
te_results <- transfer_entropy(
  x = sim_data$口コミ数_X,
  y = sim_data$投稿数_Y,
  lx = 1,
  ly = 1,
  nboot = 100,
  quiet = TRUE,
  seed = seed
)

# 計算結果のサマリーを表示
cat("--------------------------------------------------\n")
cat("Transfer Entropy 計算結果サマリー\n")
cat("--------------------------------------------------\n")
summary(te_results)

--------------------------------------------------
Transfer Entropy 計算結果サマリー
--------------------------------------------------
Shannon's Transfer Entropy

Coefficients:
           te      ete     se p-value    
X->Y 0.019167 0.000000 0.0110    0.48    
Y->X 0.148847 0.123193 0.0111  <2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Bootstrapped TE Quantiles (100 replications):
Direction      0%     25%     50%     75%    100%
     X->Y  0.0021  0.0134  0.0190  0.0249  0.0635
     Y->X  0.0031  0.0121  0.0196  0.0282  0.0545 

Number of Observations: 200

           te      ete     se p-value  
Y->X 0.148847 0.123193 0.0111  <2e-16 ***

           te      ete     se p-value  
X->Y 0.019167 0.000000 0.0110    0.48