Rで 標準偏差と標準誤差の違い を確認します。
1. 標準偏差と標準誤差とは
標準偏差と標準誤差は、どちらもデータの「ばらつき」を表す指標ですが、その目的と対象が根本的に異なります。
標準偏差 (Standard Deviation, SD)
目的: 1つのサンプル(または母集団)に含まれるデータそのもののばらつきの大きさを測る指標です。個々のデータ点が、そのサンプルの平均からどれだけ離れているかの平均的な度合いを示します。
数式: サンプルサイズが \(n\)、個々のデータが \(x_i\)、標本平均が \(\bar{x}\) のとき、標本標準偏差 \(s\) は、母分散の不偏推定量である不偏分散 \(s^2\) の平方根として定義されるのが一般的です。
不偏分散 \(s^2\): \[ s^2 = \dfrac{1}{n-1} \displaystyle\sum_{i=1}^{n} \left(x_i - \bar{x}\right)^2 \]
標本標準偏差 \(s\) (不偏分散の平方根): \[ s = \sqrt{\dfrac{1}{n-1} \displaystyle\sum_{i=1}^{n} \left(x_i - \bar{x}\right)^2} \]
標準誤差 (Standard Error, SE)
目的: 標本から計算された統計量(標本平均、標本比率など)の推定の精度を測る指標です。つまり、母集団から何度もサンプリングした場合に、その都度計算される統計量がどの程度ばらつくか(変動するか)を示します。これは「統計量の標準偏差」と言い換えることができます。
数式: ここでは最も代表的な例として、標本平均の標準誤差(Standard Error of the Mean, SEM)を見てみましょう。母集団の標準偏差が \(\sigma\)、サンプルサイズが \(n\) のとき、標本平均の標準誤差は以下で定義されます。
\[ SE_{\bar{x}} = \dfrac{\sigma}{\sqrt{n}} \]
しかし、通常は母集団の標準偏差 \(\sigma\) は未知です。そのため、代わりに標本標準偏差 \(s\) を用いて推定します。
\[ \hat{SE}_{\bar{x}} = \dfrac{s}{\sqrt{n}} \]
ポイント:
- これは、標本平均のような統計量の推定値が、どれだけ信頼できるか(ばらつくか)を示します。
- サンプルサイズ \(n\) が大きくなるほど、分母が大きくなるため標準誤差は小さくなります。これは、サンプルサイズが大きいほど、その統計量が母集団の真の値をより正確に推定できることを意味します。
まとめ
| 項目 | 標準偏差 (Standard Deviation) | 標準誤差 (Standard Error) |
|---|---|---|
| 目的 | データそのもののばらつきを測る | 標本から得られた統計量の推定の精度を測る |
| 対象 | 1つのサンプル内の個々のデータ点 | 複数回のサンプリングで得られる統計量(標本平均など) |
| 意味 | 「データのばらつき」 | 「統計量のばらつき(推定の不確実性)」 |
| サンプルサイズとの関係 | \(n\) が大きくなっても値はあまり変わらない | \(n\) が大きくなると小さくなる |
2. R言語によるシミュレーション
このシミュレーションでは、以下の流れで標準偏差と標準誤差の違いを視覚的に理解します。今回は、統計量の中でも最も代表的で理解しやすい「標本平均」を例に挙げて、そのばらつき(標準誤差)がサンプルサイズによってどう変わるかを見ていきます。
- 母集団の定義: 平均50、標準偏差10の正規分布に従うデータセットを「母集団」とします。
- サンプリングの実行:
- 小さいサンプルサイズ(n=10)で何度もサンプリング(1000回)し、各サンプルの「平均」と「標準偏差」を記録します。
- 大きいサンプルサイズ(n=100)で同様にサンプリングし、記録します。
- 結果の比較:
- 各サンプルの「標準偏差」の平均値が、サンプルサイズによらず母集団の標準偏差に近いことを確認します。
- 各サンプルの「平均」のばらつき(=標本平均の標準誤差)が、サンプルサイズが大きいほど小さくなることを確認し、プロットで可視化します。
シミュレーションコード
# 必要なライブラリを読み込む
library(ggplot2)
library(dplyr)
# 乱数のシードを固定
seed <- 20250802
set.seed(seed)
# 1. 母集団の定義
# 平均50, 標準偏差10の正規分布に従う10万個のデータ
population_mean <- 50
population_sd <- 10
population_data <- rnorm(100000, mean = population_mean, sd = population_sd)
# 母集団の実際の平均と標準偏差を確認
cat("--- 母集団の情報 ---\n\n")
cat(paste0("母集団の真の平均: ", population_mean, "\n"))
cat(paste0("母集団の真の標準偏差: ", population_sd, "\n\n"))
# 2. シミュレーションの設定
n_sim <- 1000 # シミュレーション(サンプリング)の回数
n_small <- 10 # 小さいサンプルサイズ
n_large <- 100 # 大きいサンプルサイズ
# 3. シミュレーションの実行
# 小さいサンプルサイズ (n=10) でのシミュレーション
# replicate関数を使い、1000回サンプリングを繰り返す
results_small <- replicate(n_sim, {
# 母集団からn_small個のデータをランダムにサンプリング
sample_data <- sample(population_data, n_small)
# サンプルの平均と標準偏差を計算(sd()は分母n-1で計算される)
c(mean = mean(sample_data), sd = sd(sample_data))
})
# 大きいサンプルサイズ (n=100) でのシミュレーション
results_large <- replicate(n_sim, {
# 母集団からn_large個のデータをランダムにサンプリング
sample_data <- sample(population_data, n_large)
# サンプルの平均と標準偏差を計算(sd()は分母n-1で計算される)
c(mean = mean(sample_data), sd = sd(sample_data))
})
# 結果をデータフレームに変換
# t()で行と列を入れ替える
df_small <- as.data.frame(t(results_small))
df_large <- as.data.frame(t(results_large))
# 4. 結果の分析と出力
cat("--- シミュレーション結果の分析 ---\n\n")
# << 標準偏差の比較 >>
# 各シミュレーションで得られた1000個の「標本標準偏差」の平均値
mean_sd_small <- mean(df_small$sd)
mean_sd_large <- mean(df_large$sd)
cat("<< 標準偏差 (個々のサンプルのばらつき) の比較 >>\n\n")
cat(paste0("サンプルサイズ n=", n_small, " の場合、標本標準偏差の平均値は ", round(mean_sd_small, 3), " です。\n"))
cat(paste0("サンプルサイズ n=", n_large, " の場合、標本標準偏差の平均値は ", round(mean_sd_large, 3), " です。\n"))
cat(paste0("→ サンプルサイズが大きくなっても、標本標準偏差の値自体は母集団の標準偏差(", population_sd, ")から大きくは変わりません。\n\n"))
# << 標準誤差の比較 >>
# ここでは統計量として「標本平均」を扱っています
# (A) シミュレーションから直接計算した標準誤差(=1000個の標本平均の標準偏差)
se_sim_small <- sd(df_small$mean)
se_sim_large <- sd(df_large$mean)
# (B) 理論式から計算した標準誤差 (s / sqrt(n))
# 1000個のサンプルから計算した標準誤差の平均値
se_formula_small <- mean(df_small$sd / sqrt(n_small))
se_formula_large <- mean(df_large$sd / sqrt(n_large))
cat("<< 標本平均の標準誤差 (標本平均のばらつき) の比較 >>\n\n")
cat(paste0("サンプルサイズ n=", n_small, " の場合:\n"))
cat(paste0(" (A) 標本平均の標準偏差(シミュレーションによるSE): ", round(se_sim_small, 3), "\n"))
cat(paste0(" (B) 式(s/√n)から求めたSEの平均値 : ", round(se_formula_small, 3), "\n\n"))
cat(paste0("サンプルサイズ n=", n_large, " の場合:\n"))
cat(paste0(" (A) 標本平均の標準偏差(シミュレーションによるSE): ", round(se_sim_large, 3), "\n"))
cat(paste0(" (B) 式(s/√n)から求めたSEの平均値 : ", round(se_formula_large, 3), "\n\n"))
cat("→ サンプルサイズが大きくなると、標本平均のばらつき(標準誤差)は明らかに小さくなります。\n")
cat("→ サンプルサイズの大小に関わらず、シミュレーションで得られた標本平均のばらつき(A)は、理論式(B)とほぼ一致します。\n\n")
# 5. 結果のプロット
# プロット用のデータフレームを作成
plot_data <- bind_rows(
mutate(df_small, sample_size = paste0("n = ", n_small)),
mutate(df_large, sample_size = paste0("n = ", n_large))
) %>%
# 凡例の順序をnが小さい順にする
mutate(sample_size = factor(sample_size, levels = c(paste0("n = ", n_small), paste0("n = ", n_large))))
# ggplotで標本平均の分布を可視化
g <- ggplot(plot_data, aes(x = mean, fill = sample_size)) +
# 密度プロットを半透明で描画
geom_density(alpha = 0.6, color = "black") +
# 母集団の真の平均を黒の破線で示す
geom_vline(
xintercept = population_mean,
color = "black",
linetype = "dashed",
linewidth = 1
) +
# 凡例とラベルの設定
labs(
title = "標本平均の分布とサンプルサイズ",
subtitle = "サンプルサイズが大きくなると、標本平均のばらつき(=標準誤差)が小さくなる様子",
x = "標本平均",
y = "密度",
fill = "サンプルサイズ"
) +
theme_minimal(base_size = 14) +
theme(legend.position = "bottom")
# プロットを表示
print(g)--- 母集団の情報 ---
母集団の真の平均: 50
母集団の真の標準偏差: 10
--- シミュレーション結果の分析 ---
<< 標準偏差 (個々のサンプルのばらつき) の比較 >>
サンプルサイズ n=10 の場合、標本標準偏差の平均値は 9.71 です。
サンプルサイズ n=100 の場合、標本標準偏差の平均値は 10.012 です。
→ サンプルサイズが大きくなっても、標本標準偏差の値自体は母集団の標準偏差(10)から大きくは変わりません。
<< 標本平均の標準誤差 (標本平均のばらつき) の比較 >>
サンプルサイズ n=10 の場合:
(A) 標本平均の標準偏差(シミュレーションによるSE): 3.199
(B) 式(s/√n)から求めたSEの平均値 : 3.071
サンプルサイズ n=100 の場合:
(A) 標本平均の標準偏差(シミュレーションによるSE): 0.963
(B) 式(s/√n)から求めたSEの平均値 : 1.001
→ サンプルサイズが大きくなると、標本平均のばらつき(標準誤差)は明らかに小さくなります。
→ サンプルサイズの大小に関わらず、シミュレーションで得られた標本平均のばらつき(A)は、理論式(B)とほぼ一致します。シミュレーション結果の解説
- 標準偏差の比較: サンプルサイズが10でも100でも、そこから計算される標本標準偏差の平均値は、母集団の真の標準偏差である10に近い値(9.71, 10.012)になっています。これは、標準偏差が「データそのもののばらつき」を反映していることを示しています。
- 標準誤差の比較: 1000回サンプリングして得られた標本平均のばらつき(
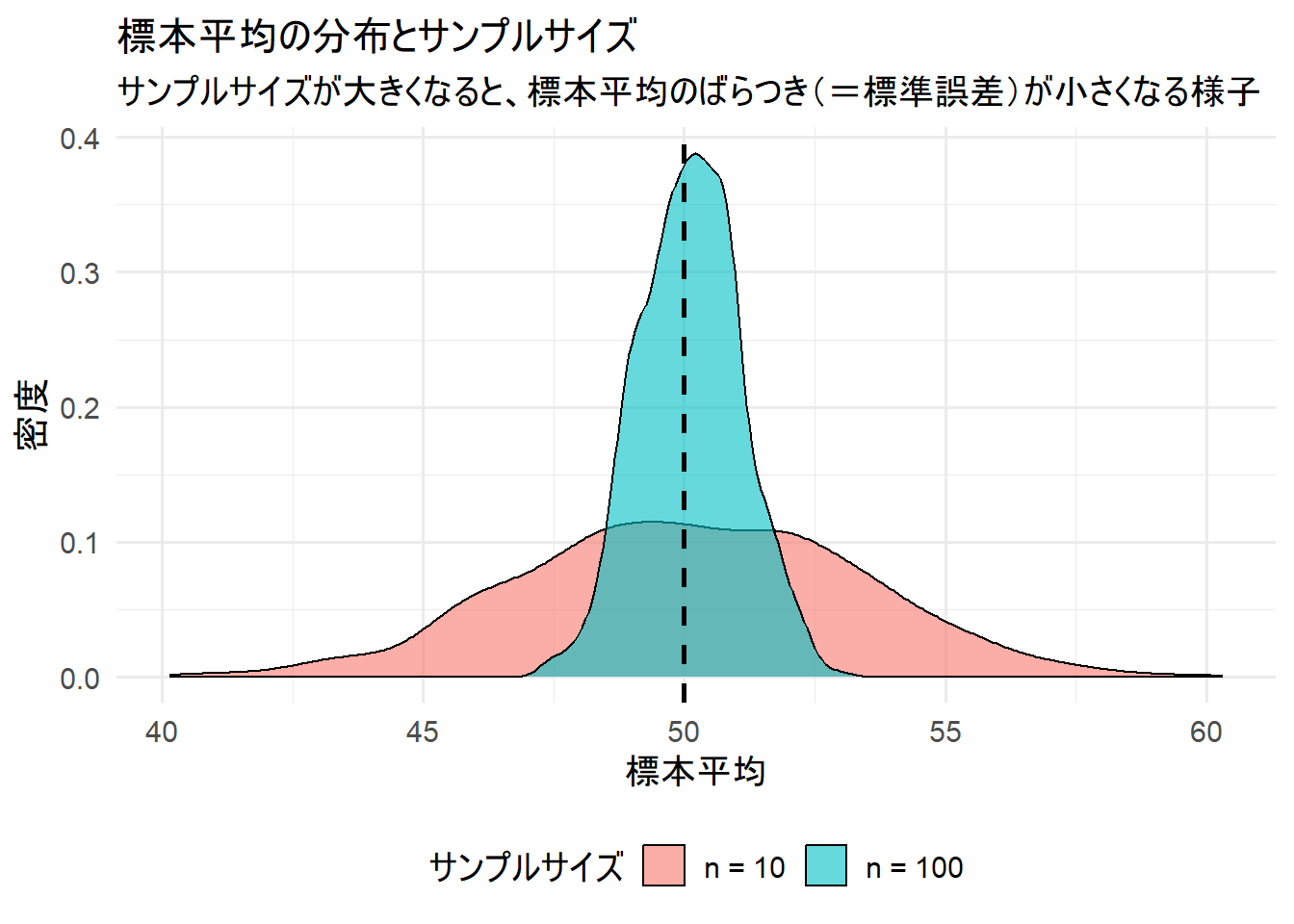
sd(df_small$mean)など)は、サンプルサイズが n=10 のとき約3.199、n=100のとき約0.963と、サンプルサイズが大きいほど小さくなっています。これが標本平均の標準誤差です。この値は、各サンプルから計算した理論式s/√nの平均値ともほぼ一致しており、理論とシミュレーションが整合していることがわかります。 - Figure 1 は、統計量の一例である「標本平均」が、1000回のサンプリングでどのような分布になったかを示しています。
-
n=10(赤色)の分布は、横に広く広がっています。これは、サンプルサイズが小さいと、得られる標本平均が大きくばらつく(=標準誤差が大きい)ことを意味します。 -
n=100(青色)の分布は、n=10と比較して、中心(母平均50)の周りに鋭く尖っています。これは、サンプルサイズが大きいと、得られる標本平均のばらつきが小さく(=標準誤差が小さい)、より母平均に近い値をとりやすいことを意味します。 - 中央の黒い破線は母集団の真の平均(50)です。どちらの分布もこの真の平均を中心に分布していることがわかります。
このシミュレーションを通じて、「標準偏差」は個々のサンプルのデータの広がりを指し、「標準誤差」は標本平均のような統計量の信頼性(ばらつき)を指す、という違いを直感的に理解することができます。
以上です。