Rで機械学習:サポートベクターマシン

# 再現性のための乱数シード設定
seed <- 20250810
set.seed(seed)

# データ生成
n <- 50 # 各クラスのデータ数
# フジリンゴのデータ (糖度が高く、硬度もやや高い)
fuji_apple <- data.frame(
  sugar = rnorm(n, mean = 15, sd = 1.5),
  hardness = rnorm(n, mean = 8, sd = 1),
  class = "フジリンゴ"
)
# オウシュウナシのデータ (糖度がやや低く、硬度も低い)
oushu_pear <- data.frame(
  sugar = rnorm(n, mean = 12, sd = 1.5),
  hardness = rnorm(n, mean = 5, sd = 1),
  class = "オウシュウナシ"
)

# データを結合
fruit_data <- rbind(fuji_apple, oushu_pear)
fruit_data$class <- as.factor(fruit_data$class)

# SVMモデルの学習 (線形カーネル)
svm_linear <- svm(class ~ ., data = fruit_data, kernel = "linear", scale = TRUE)

# サポートベクターを特定
support_vectors <- fruit_data[svm_linear$index, ]
cat(paste("学習の結果、", nrow(support_vectors), "個のサポートベクターが特定されました。\n\n"))

# 決定境界とマージンをプロットするためのグリッドを作成
grid_range <- apply(fruit_data[, 1:2], 2, range)
x_grid <- seq(from = grid_range[1, 1], to = grid_range[2, 1], length.out = 100)
y_grid <- seq(from = grid_range[1, 2], to = grid_range[2, 2], length.out = 100)
grid_df <- expand.grid(sugar = x_grid, hardness = y_grid)

# グリッドの各点での予測値（決定境界からの距離）を計算
pred_values <- predict(svm_linear, grid_df, decision.values = TRUE)
decision_values <- as.vector(attr(pred_values, "decision.values"))

grid_df$decision_values <- decision_values

# プロットの作成
p1 <- ggplot(data = fruit_data, aes(x = sugar, y = hardness)) +
  # 決定境界とマージンを等高線で描画
  geom_contour(data = grid_df, aes(z = decision_values), breaks = 0, color = "black", linewidth = 1, linetype = "solid") +
  geom_contour(data = grid_df, aes(z = decision_values), breaks = c(-1, 1), color = "black", linewidth = 0.5, linetype = "dashed") +
  # 元のデータをプロット
  geom_point(aes(color = class, shape = class), size = 3) +
  # サポートベクターを強調表示
  geom_point(data = support_vectors, aes(x = sugar, y = hardness), shape = 21, size = 5, fill = NA, stroke = 1.5, color = "blue") +
  scale_color_manual(values = c("フジリンゴ" = "red", "オウシュウナシ" = "darkgreen")) +
  scale_shape_manual(values = c("フジリンゴ" = 16, "オウシュウナシ" = 17)) +
  labs(
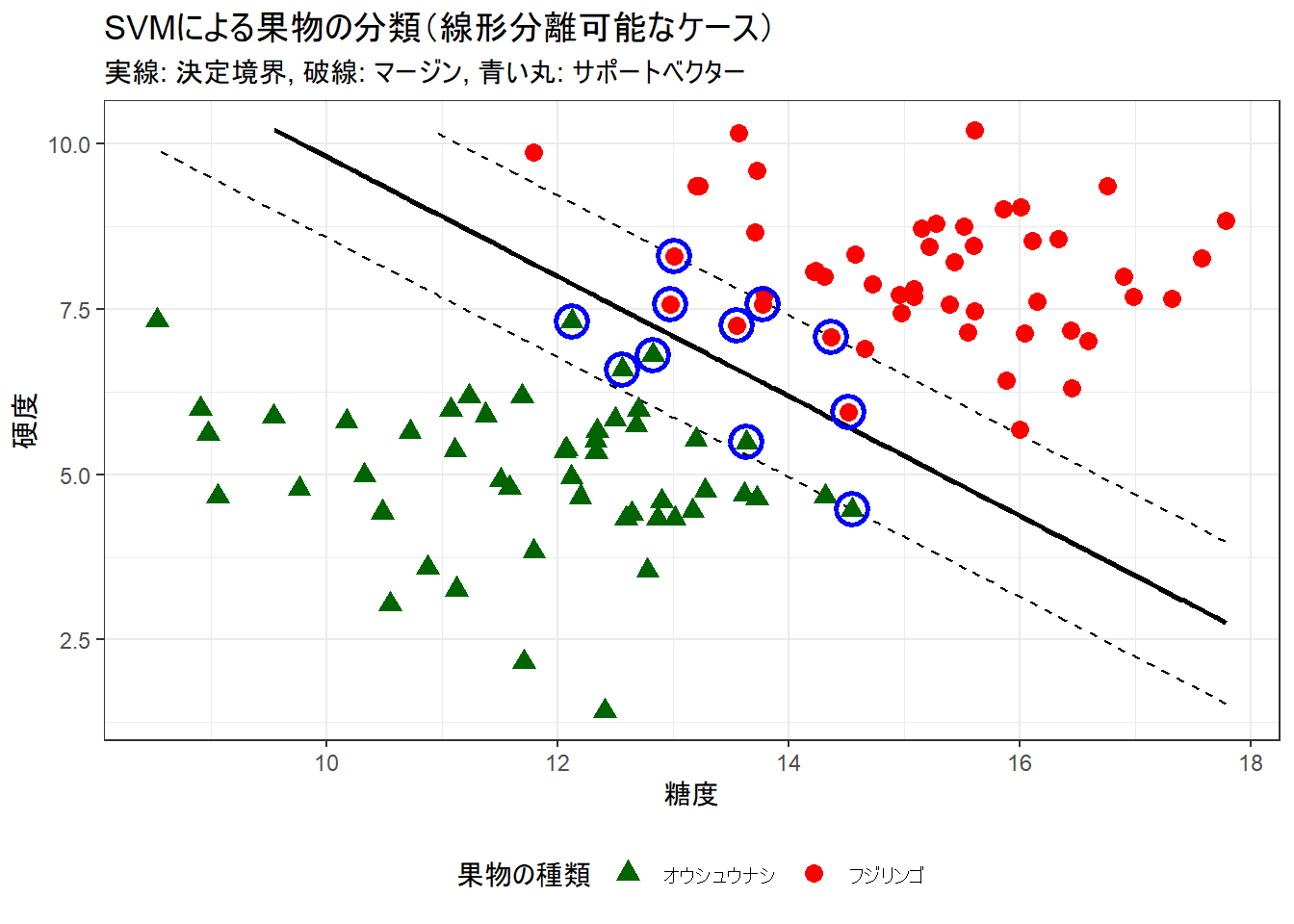
    title = "SVMによる果物の分類（線形分離可能なケース）",
    subtitle = "実線: 決定境界, 破線: マージン, 青い丸: サポートベクター",
    x = "糖度",
    y = "硬度",
    color = "果物の種類",
    shape = "果物の種類"
  ) +
  theme_bw() +
  theme(legend.position = "bottom")

print(p1)

# 再現性のための乱数シード設定
set.seed(seed)

# ドーナツ状のデータ生成
n <- 100 # 各クラスのデータ数
# フジリンゴのデータ (中心部)
center_apple <- data.frame(
  r = rnorm(n, mean = 1, sd = 0.5),
  t = runif(n, 0, 2 * pi)
) %>% mutate(
  sugar = r * cos(t) + 13,
  hardness = r * sin(t) + 6,
  class = "フジリンゴ"
)

# オウシュウナシのデータ (外側)
outer_pear <- data.frame(
  r = rnorm(n, mean = 4, sd = 0.7),
  t = runif(n, 0, 2 * pi)
) %>% mutate(
  sugar = r * cos(t) + 13,
  hardness = r * sin(t) + 6,
  class = "オウシュウナシ"
)

# データを結合
fruit_data_nonlinear <- rbind(
  center_apple[, c("sugar", "hardness", "class")],
  outer_pear[, c("sugar", "hardness", "class")]
)
fruit_data_nonlinear$class <- as.factor(fruit_data_nonlinear$class)

# SVMモデルの学習 (RBFカーネル)
# gammaとcostは最適な値を探す必要がありますが、ここでは良い結果が得られる値を指定します
svm_rbf <- svm(class ~ ., data = fruit_data_nonlinear, kernel = "radial", gamma = 0.5, cost = 1, scale = TRUE)

# サポートベクターを特定
support_vectors_rbf <- fruit_data_nonlinear[svm_rbf$index, ]
cat(paste("学習の結果、", nrow(support_vectors_rbf), "個のサポートベクターが特定されました。\n\n"))

# 決定境界プロット用のグリッドを作成
grid_range_nl <- apply(fruit_data_nonlinear[, 1:2], 2, range)
x_grid_nl <- seq(from = grid_range_nl[1, 1], to = grid_range_nl[2, 1], length.out = 100)
y_grid_nl <- seq(from = grid_range_nl[1, 2], to = grid_range_nl[2, 2], length.out = 100)
grid_df_nl <- expand.grid(sugar = x_grid_nl, hardness = y_grid_nl)

# グリッドの各点で予測
# RBFカーネルの場合、マージンは決定境界からの距離1とは限らないため、背景色で領域を表現します
grid_df_nl$predicted_class <- predict(svm_rbf, grid_df_nl)

# プロットの作成
p2 <- ggplot(data = fruit_data_nonlinear, aes(x = sugar, y = hardness)) +
  # 予測領域を背景色で描画
  geom_raster(data = grid_df_nl, aes(fill = predicted_class), alpha = 0.3, interpolate = TRUE) +
  # 元のデータをプロット
  geom_point(aes(color = class, shape = class), size = 3) +
  # サポートベクターを強調表示
  geom_point(data = support_vectors_rbf, aes(x = sugar, y = hardness), shape = 21, size = 5, fill = NA, stroke = 1.5, color = "blue") +
  scale_color_manual(values = c("フジリンゴ" = "red", "オウシュウナシ" = "darkgreen")) +
  scale_fill_manual(values = c("フジリンゴ" = "red", "オウシュウナシ" = "darkgreen")) +
  scale_shape_manual(values = c("フジリンゴ" = 16, "オウシュウナシ" = 17)) +
  guides(fill = "none") + # 背景色の凡例は非表示
  labs(
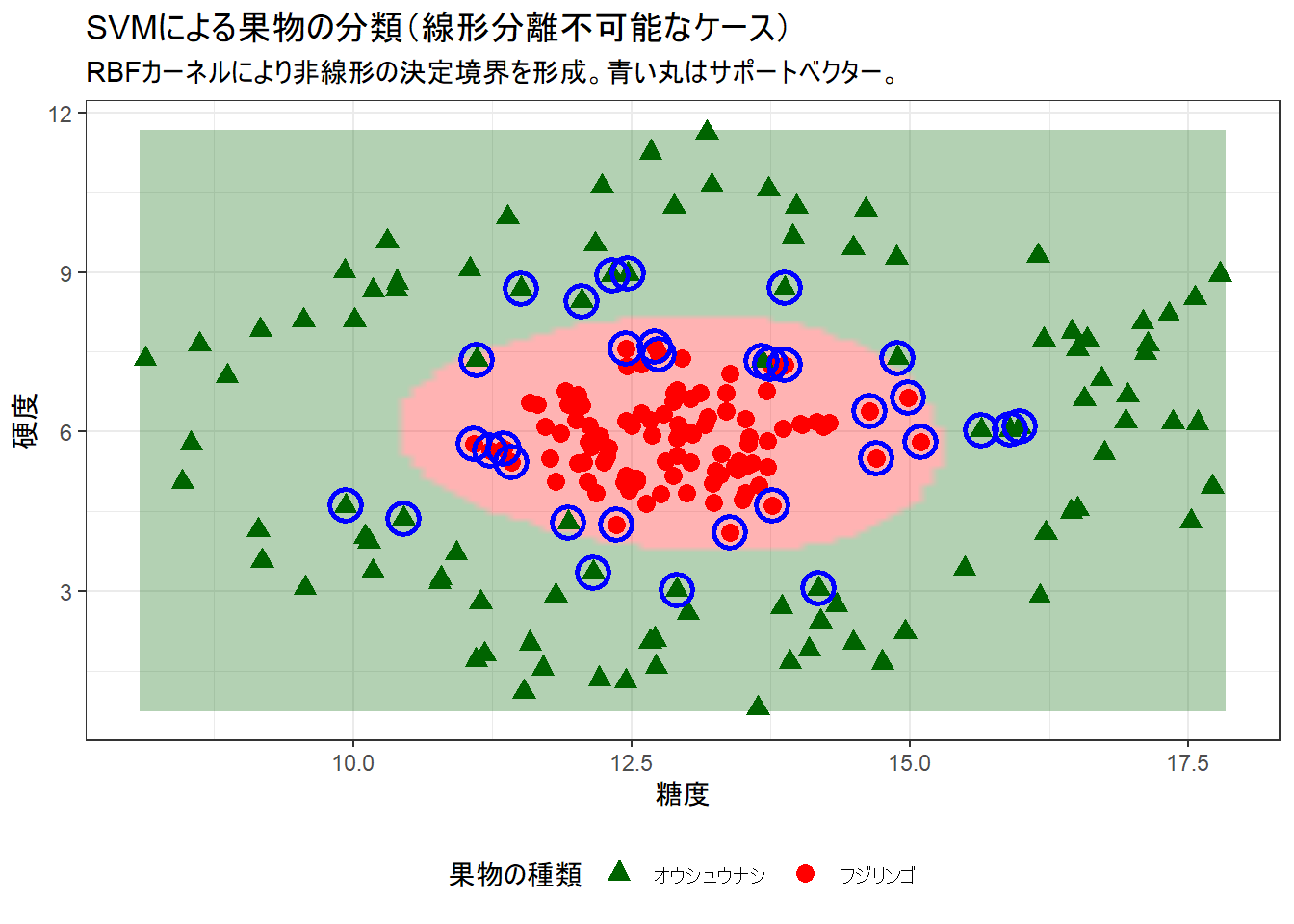
    title = "SVMによる果物の分類（線形分離不可能なケース）",
    subtitle = "RBFカーネルにより非線形の決定境界を形成。青い丸はサポートベクター。",
    x = "糖度",
    y = "硬度",
    color = "果物の種類",
    shape = "果物の種類"
  ) +
  theme_bw() +
  theme(legend.position = "bottom")

print(p2)