Rで 機械学習:ナイーブベイズ を試みます。
本ポストはこちらの続きです。

1. ナイーブベイズ(Naive Bayes)とは
ナイーブベイズは、ベイズの定理を基礎とした分類アルゴリズムです。特に、迷惑メールフィルタや文書分類といったテキスト分類の分野で古くから利用されてきました。
ベイズの定理
ナイーブベイズの根幹をなすベイズの定理は、ある事象が起きたという結果(観測)から、その原因である確率を求めるための定理であり、以下のように表されます。
\[P\left(Y|X\right) = \dfrac{P\left(X|Y\right)P\left(Y\right)}{P\left(X\right)}\]
これを分類問題に当てはめると、各要素は以下のように解釈できます。
- \(P\left(Y|X\right)\):事後確率。データ \(X\) が観測されたときに、それがクラス \(Y\) である確率。私たちが求めたい確率です。(例:あるメールの特徴 \(X\) を見たとき、それがスパムである確率)
- \(P\left(X|Y\right)\):尤度(ゆうど)。クラス \(Y\) であるという前提のもとで、データ \(X\) が観測される確率。(例:スパムメールである場合、そのメールが「セール」という単語を含む確率)
- \(P\left(Y\right)\):事前確率。データを見る前に、クラス \(Y\) が発生する確率。(例:全てのメールのうち、スパムメールが占める割合)
- \(P\left(X\right)\):データ \(X\) が観測される確率。これは確率を正規化するための定数であり、分類の際には大小比較が重要なので、計算上は無視されることが多いです。
「ナイーブ(Naive)」である理由
ナイーブベイズの「ナイーブ」という名前は、「すべての特徴量は、互いに独立である」という仮定に由来します。
例えば、迷惑メールフィルタで「セール」という単語と「当選」という単語を特徴量として使う場合、ナイーブベイズは「セール」という単語が出現するかどうかと、「当選」という単語が出現するかどうかは、互いに全く影響を与えない無関係な事象である、と仮定します。
現実には、これらの単語は同じメールで使われることが多い(関連がある)ため、この仮定は正しくありません。しかし、この「ナイーブ」な仮定を置くことで、計算が単純化されます。さらに、この仮定が現実と異なっていても、多くの場合で充分な分類性能を発揮することが知られています。
この仮定により、複数の特徴量 \(X = (X_1, X_2, ..., X_n)\) を持つデータに対する事後確率は、以下のように単純な確率の積で計算できます。
\[P\left(Y|X_1, ..., X_n\right) \propto P\left(Y\right) \displaystyle\prod_{i=1}^{n} P\left(X_i|Y\right)\]
ナイーブベイズ分類器は、全てのクラスについてこの値を計算し、最も値が大きくなったクラスにデータを分類します。
2. シミュレーションのシナリオ
舞台: あなたが開発者として働くメールサービス会社
あなたは、自社のメールサービスに搭載する「迷惑メールフィルタ」を開発するよう任されました。手元には、過去のメールが「迷惑メール(スパム)」か「通常メール(ハム)」かに分類されたデータセットがあります。
このデータセットを使って、ナイーブベイズ分類器を学習させ、新しく届いたメールが迷惑メールかどうかを自動で判定するシステムを構築します。
分析に使用する特徴量(メールの内容や属性から判断):
-
has_sale: メール本文に「セール」、「限定」、「割引」といった単語が含まれるか (はい/いいえ) -
has_prize: メール本文に「当選」、「賞品」、「無料」といった単語が含まれるか (はい/いいえ) -
has_urgent: メール本文に「緊急」、「至急」、「警告」といった単語が含まれるか (はい/いいえ) -
is_unknown_sender: 送信者がアドレス帳に登録されていない未知の相手か (はい/いいえ)
シナリオのステップ:
- 学習フェーズ(確率の計算):
- 既存のメールデータセットから、ナイーブベイズが必要とする事前確率と条件付き確率(尤度)を計算します。
- 具体的には、「全メールのうちスパムが占める割合は?(事前確率)」や、「スパムメールの中で『セール』という単語が含まれる割合は?(条件付き確率)」などを学習します。
- 予測フェーズ(確率の比較):
- 特徴が
(has_sale=はい, has_prize=はい, has_urgent=いいえ, is_unknown_sender=はい)という新しいメールが届いたとします。 - 学習した確率をベイズの定理に当てはめ、「このメールがスパムである確率(の高さ)」と「ハムである確率(の高さ)」をそれぞれ計算します。
- 2つの値を比較し、より値が大きい方にこのメールを分類します。
- 特徴が
3. R言語によるシミュレーションコード
準備:必要なライブラリの読み込み
# ライブラリの読み込み
library(e1071)
library(ggplot2)
library(dplyr)
library(tidyr)ステップ1:学習フェーズ(確率の計算)
# 再現性のための乱数シード設定
seed <- 20250815
set.seed(seed)
# データ生成
# 迷惑メールと通常メールのデータセットを生成します。
n_spam <- 400 # スパムメールの数
n_ham <- 600 # 通常メール(ハム)の数
total_mails <- n_spam + n_ham
# スパムメールのデータ (特定の単語が出やすい)
spam_mails <- data.frame(
has_sale = factor(sample(c("はい", "いいえ"), n_spam, replace = TRUE, prob = c(0.7, 0.3))),
has_prize = factor(sample(c("はい", "いいえ"), n_spam, replace = TRUE, prob = c(0.6, 0.4))),
has_urgent = factor(sample(c("はい", "いいえ"), n_spam, replace = TRUE, prob = c(0.4, 0.6))),
is_unknown_sender = factor(sample(c("はい", "いいえ"), n_spam, replace = TRUE, prob = c(0.8, 0.2))),
type = "スパム"
)
# ハムメールのデータ (特定の単語が出にくい)
ham_mails <- data.frame(
has_sale = factor(sample(c("はい", "いいえ"), n_ham, replace = TRUE, prob = c(0.05, 0.95))),
has_prize = factor(sample(c("はい", "いいえ"), n_ham, replace = TRUE, prob = c(0.01, 0.99))),
has_urgent = factor(sample(c("はい", "いいえ"), n_ham, replace = TRUE, prob = c(0.1, 0.9))),
is_unknown_sender = factor(sample(c("はい", "いいえ"), n_ham, replace = TRUE, prob = c(0.3, 0.7))),
type = "ハム"
)
mail_data <- rbind(spam_mails, ham_mails)
# ナイーブベイズモデルを学習させ、必要な確率を計算します
# type列を目的変数、他の全てを説明変数としてモデルを学習
nb_model <- naiveBayes(type ~ ., data = mail_data)
cat("計算された確率テーブルを表示\n")
print(nb_model)計算された確率テーブルを表示
Naive Bayes Classifier for Discrete Predictors
Call:
naiveBayes.default(x = X, y = Y, laplace = laplace)
A-priori probabilities:
Y
スパム ハム
0.4 0.6
Conditional probabilities:
has_sale
Y いいえ はい
スパム 0.28750000 0.71250000
ハム 0.94666667 0.05333333
has_prize
Y いいえ はい
スパム 0.38 0.62
ハム 0.99 0.01
has_urgent
Y いいえ はい
スパム 0.5750000 0.4250000
ハム 0.8933333 0.1066667
is_unknown_sender
Y いいえ はい
スパム 0.1625000 0.8375000
ハム 0.6883333 0.3116667学習結果の解説:
- A-priori probabilities (事前確率): データ全体における各クラスの割合です。P(ハム)が60%、P(スパム)が40%と設定どおりです。
- Conditional probabilities (条件付き確率): 各クラスであるという条件下で、それぞれの特徴が「はい」または「いいえ」になる確率(尤度)です。例えば、
has_saleの表を見ると、スパムメールの場合に「はい」となる確率は約71.3%ですが、ハムメールの場合は5.3%です。ナイーブベイズは、この確率の差を利用してメールを分類します。
ステップ2:予測フェーズ(確率の比較)
# 新しいメールのデータを作成
new_mail <- data.frame(
has_sale = factor("はい", levels = c("はい", "いいえ")),
has_prize = factor("はい", levels = c("はい", "いいえ")),
has_urgent = factor("いいえ", levels = c("はい", "いいえ")),
is_unknown_sender = factor("はい", levels = c("はい", "いいえ"))
)
cat("以下の特徴を持つ新しいメールが届きました:\n")
print(new_mail)
cat("\nこのメールが「スパム」である確率と「ハム」である確率を計算します。\n")
# type="raw"を指定すると、各クラスに属する事後確率を返す
prediction_probs <- predict(nb_model, new_mail, type = "raw")
cat("\n■ 予測された確率:\n")
print(prediction_probs)
final_prediction <- predict(nb_model, new_mail)
cat("\n■ 最終的な分類結果:\n")
cat("確率を比較した結果、このメールは「", as.character(final_prediction), "」に分類されました。\n")以下の特徴を持つ新しいメールが届きました:
has_sale has_prize has_urgent is_unknown_sender
1 はい はい いいえ はい
このメールが「スパム」である確率と「ハム」である確率を計算します。
■ 予測された確率:
スパム ハム
[1,] 0.9989541 0.001045948
■ 最終的な分類結果:
確率を比較した結果、このメールは「 スパム 」に分類されました。計算過程の解説:
- P(スパム|新しいメール) に比例する値:
\[\begin{eqnarray}
&&\text{P(スパム) × P(sale=はい|スパム) × P(prize=はい|スパム) × P(urgent=いいえ|スパム) × P(unknown=はい|スパム)}\\
&&= \text{0.40 × 0.7125 × 0.62 × 0.575 × 0.8375}\\
&&= \text{0.085092}
\end{eqnarray}\]
- P(ハム|新しいメール) に比例する値:
\[\begin{eqnarray}
&&\text{P(ハム) × P(sale=はい|ハム) × P(prize=はい|ハム) × P(urgent=いいえ|ハム) × P(unknown=はい|ハム)}\\
&&=\text{0.60 × 0.0533 × 0.01 × 0.8933 × 0.3117}\\
&&=\text{0.000089}
\end{eqnarray}\]
計算の結果、スパムである確率の方が高いため、このメールは「スパム」と分類されます。
predict関数が返す確率は、これらの値を合計が1になるように正規化したものです。
正規化後のスパム確率: 0.085092 / (0.085092 + 0.000089) = 0.9989552
これは、predict関数が出力したスパムの確率(0.9989541)と一致します(四捨五入における差異あり)。
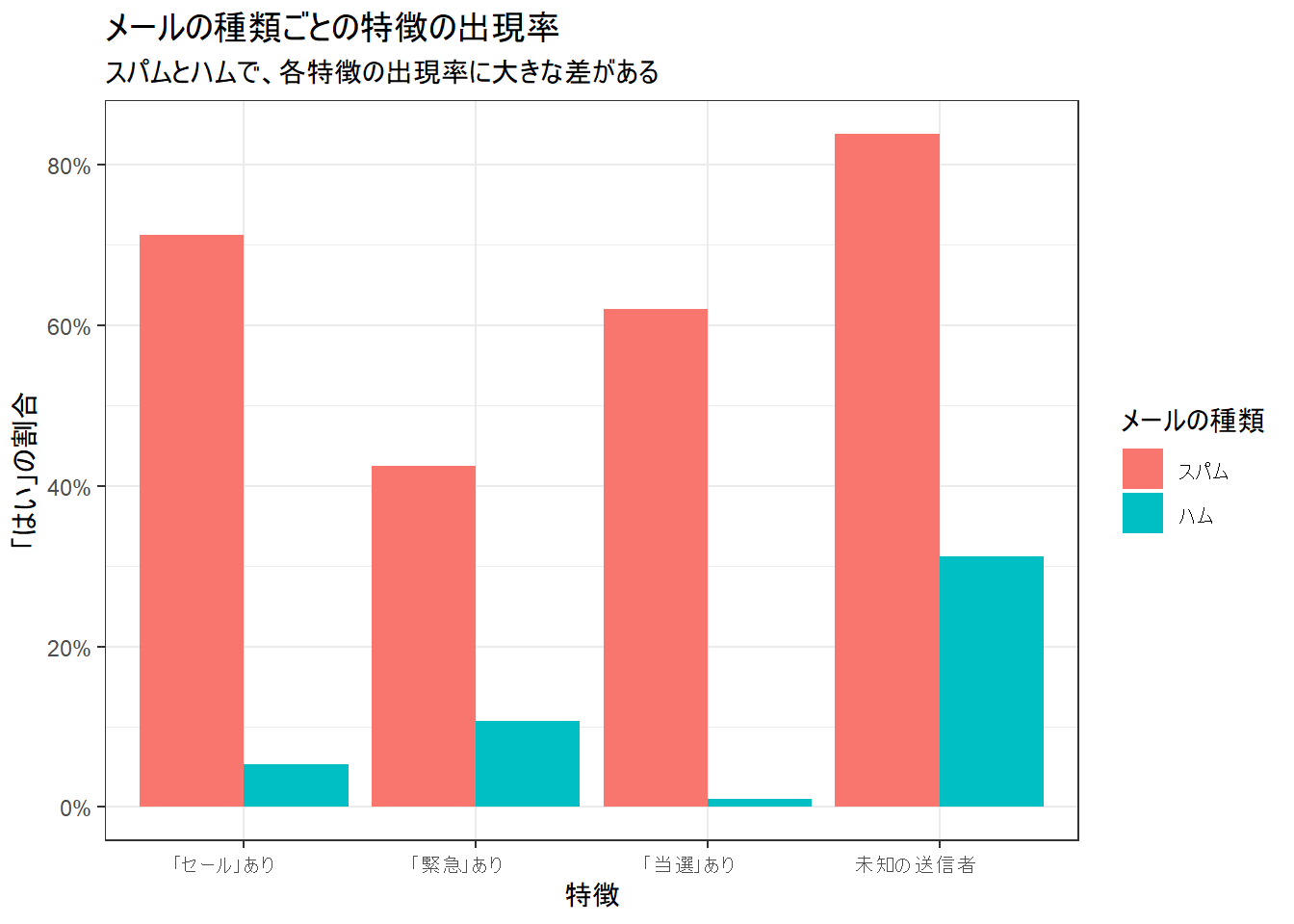
【補足】特徴量の分布の可視化
学習に使ったデータにおいて、各特徴量がスパムとハムでどれだけ出現率が違うのかを可視化します。
# データを整形
plot_data <- mail_data %>%
pivot_longer(cols = -type, names_to = "feature", values_to = "value") %>%
group_by(type, feature, value) %>%
summarise(count = n(), .groups = "drop") %>%
group_by(type, feature) %>%
mutate(proportion = count / sum(count)) %>%
filter(value == "はい") %>%
mutate(feature_jp = case_when(
feature == "has_sale" ~ "「セール」あり",
feature == "has_prize" ~ "「当選」あり",
feature == "has_urgent" ~ "「緊急」あり",
feature == "is_unknown_sender" ~ "未知の送信者"
))
# 棒グラフで可視化
p_features <- ggplot(plot_data, aes(x = feature_jp, y = proportion, fill = type)) +
geom_col(position = "dodge") +
scale_y_continuous(labels = scales::percent_format()) +
labs(
title = "メールの種類ごとの特徴の出現率",
subtitle = "スパムとハムで、各特徴の出現率に大きな差がある",
x = "特徴",
y = "「はい」の割合",
fill = "メールの種類"
) +
theme_bw() +
theme(axis.text.x = element_text(angle = 0, hjust = 0.7))
print(p_features)以上です。