Rで 機械学習:ランダムフォレスト を試みます。
本ポストはこちらの続きです。

1. ランダムフォレスト(Random Forest)とは
ランダムフォレストは、分類と回帰の両方に使用できる、教師あり学習のアンサンブル学習アルゴリズムです。アンサンブル学習とは、複数の学習器(モデル)を組み合わせて、単体モデルよりも高い精度や安定性を持つ一つの学習器を構築する手法です。
ランダムフォレストは、その名の通り「決定木(Decision Tree)」を多数集めて「森(Forest)」を作り、個々の木々の予測結果を統合して最終的な結論を出します。
ランダムフォレストの仕組み
ランダムフォレストは、前回のシミュレーションで見た決定木の「過学習しやすい」という弱点を克服するために、2種類の「ランダム性」を導入しています。この手法の基礎にはバギング(Bagging)という考え方があります。
1. データのランダムサンプリング(バギング)
元の訓練データから、ランダムにデータ点を復元抽出し(同じデータが何度も選ばれることを許す)、複数の異なるデータセットを作成します。これをブートストラップサンプリングと呼びます。 ランダムフォレストでは、このブートストラップサンプリングされたデータセットを使って、それぞれ異なる決定木を学習させます。これにより、多様性のある木々が生まれます。
2. 特徴量のランダムサンプリング
決定木が各ノードでデータを分割する際、通常は全ての利用可能な特徴量の中から最適な分割点を探します。 しかし、ランダムフォレストでは、全ての特徴量を使うのではなく、ランダムに選ばれた一部の特徴量の中から最適な分割点を探します。
なぜこの2つのランダム性が重要なのか?
- もし特定の影響力が強い特徴量があった場合、通常の決定木はどれも同じような構造になりがちです。
- 特徴量をランダムに制限することで、個々の木は異なる特徴量に注目せざるを得なくなり、より多様で、互いに相関の低い木が多数生成されます。
- この「多様な専門家(決定木)たち」の意見を多数決(分類の場合)や平均(回帰の場合)でまとめることで、一つの木が訓練データに過剰に適合してしまう「過学習」が抑制され、モデル全体の汎化性能が向上します。
ランダムフォレストの特徴
長所:
- 過学習しにくい: 多数決で結果を出すため、個々の木が過学習していても、その影響が全体として緩和されます。
- 特徴量の重要度がわかる: どの特徴量が予測に大きく貢献したかを数値化できます。これにより、モデルの解釈のヒントが得られます。
- 安定性が高い: 決定木と異なり、訓練データが多少変動してもモデル全体の結果は安定しています。
- OOB誤差 (Out-of-Bag Error): ブートストラップサンプリングの際に選ばれなかったデータ(Out-of-Bagサンプル)を使って、モデルの汎化性能を評価できます。これにより、別途テストデータを用意しなくてもモデルの性能を推定できます。
短所:
- 解釈性の低下: 多数の木が組み合わさっているため、決定木のように「なぜその結論に至ったのか」を単純な
if-thenルールで説明することは困難です(ブラックボックスモデル)。 - 計算コスト: 多くの木を構築するため、計算時間とメモリ消費量が大きくなることがあります。
2. シミュレーションのシナリオ
舞台: 最先端のスマート農業ファーム
あなたは、最新のセンサー技術を導入したスマート農業ファームのデータサイエンティストです。このファームでは、収穫されたトマトの品質を自動で判定し、市場に出荷する際の価格設定やブランディングに役立てるプロジェクトが進行中です。
あなたの仕事は、センサーから得られる5つの測定データを用いて、トマトが「高品質」か「標準品質」かを判定する高精度な機械学習モデルを、ランダムフォレストで構築することです。
判定に使用する特徴量(センサーデータ):
-
sugar_content(糖度): 甘さの指標。 -
acidity(酸度): 甘みとのバランスを取る酸味の指標。 -
firmness(硬度): 果肉のしっかり具合。輸送耐性にも関わる。 -
color_hue(色相): AIカメラで測定した色の鮮やかさ。 -
weight(重量): トマト一個あたりの重さ。
シナリオのステップ:
- ランダムフォレストモデルの構築と性能評価:
- 5つの特徴量を持つトマトのデータセットを使って、ランダムフォレストモデルを学習させます。
- 学習結果のサマリーを確認し、特に「OOB推定誤差率 (OOB estimate of error rate)」に注目して、モデルの汎化性能を評価します。
- 特徴量の重要度の可視化:
- モデルの学習結果から「特徴量の重要度」を算出し、プロットします。
- これにより、どのセンサーデータがトマトの品質判定に最も寄与しているのかを特定し、将来の栽培方法の改善やセンサー選定の参考にします。
- OOB誤差率の収束過程の確認:
- ランダムフォレストを構成する決定木の数を増やしていくと、OOB誤差率がどのように変化していくかをプロットします。
- これにより、ある程度の数の木があれば、モデルの性能が安定し、過学習が抑制される様子を視覚的に理解します。
3. R言語によるシミュレーションコード
それでは、シナリオに沿ってランダムフォレストのシミュレーションを実行します。
準備:必要なライブラリの読み込み
# ライブラリの読み込み
library(randomForest)
library(ggplot2)
library(dplyr)
library(tidyr)ステップ1:ランダムフォレストモデルの構築と性能評価
# 再現性のための乱数シード設定
seed <- 20250812
set.seed(seed)
# データ生成
# スマートファームで収穫されたトマトのセンサーデータを生成します。
# 特徴量は「糖度」「酸度」「硬度」「色相」「重量」の5つです。
n <- 250 # 各クラスのデータ数
# 高品質トマトのデータ
premium_tomato <- data.frame(
sugar_content = rnorm(n, mean = 8.5, sd = 0.8),
acidity = rnorm(n, mean = 0.4, sd = 0.05),
firmness = rnorm(n, mean = 12, sd = 1.0),
color_hue = rnorm(n, mean = 25, sd = 3),
weight = rnorm(n, mean = 150, sd = 15),
quality = "高品質"
)
# 標準品質トマトのデータ
standard_tomato <- data.frame(
sugar_content = rnorm(n, mean = 6.5, sd = 1.0),
acidity = rnorm(n, mean = 0.5, sd = 0.08),
firmness = rnorm(n, mean = 10, sd = 1.5),
color_hue = rnorm(n, mean = 35, sd = 5),
weight = rnorm(n, mean = 130, sd = 20),
quality = "標準品質"
)
tomato_data <- rbind(premium_tomato, standard_tomato)
tomato_data$quality <- as.factor(tomato_data$quality)
# 各特徴量の分布をバイオリンプロットで比較
tomato_data_jp <- tomato_data %>%
rename(
糖度 = sugar_content,
酸度 = acidity,
硬度 = firmness,
色相 = color_hue,
重量 = weight,
品質 = quality
)
# データをプロットしやすい「ロング形式」に変換
tomato_long <- tomato_data_jp %>%
pivot_longer(
cols = c(糖度, 酸度, 硬度, 色相, 重量),
names_to = "特徴量",
values_to = "値"
)
# バイオリンプロットの作成
p_violin <- ggplot(tomato_long, aes(x = 品質, y = 値, fill = 品質)) +
geom_violin(trim = FALSE, alpha = 0.6) + # バイオリンプロット
geom_boxplot(width = 0.15, fill = "white", outlier.shape = NA) + # 箱ひげ図を重ねる
facet_wrap(~特徴量, scales = "free_y", ncol = 5) + # 特徴量ごとにプロットを分割
scale_fill_manual(values = c("高品質" = "#F8766D", "標準品質" = "#00BFC4")) +
labs(
title = "トマトの品質別 センサーデータ分布",
subtitle = "各センサー値について「高品質」と「標準品質」の分布を比較",
x = "トマトの品質",
y = "センサー測定値"
) +
theme_bw() +
theme(
legend.position = "none", # 凡例は不要
axis.text.x = element_text(angle = 0, vjust = 0),
strip.text = element_text(size = 12)
) # 各プロットのタイトルサイズ
print(p_violin)
# GGallyパッケージのggpairs関数でペアプロットを作成
library(GGally)
p_pairs <- ggpairs(
tomato_data_jp,
columns = 1:5, # 1から5列目(特徴量)を使用
mapping = aes(color = 品質, shape = 品質, alpha = 0.7),
title = "トマトのセンサーデータ相関分析(品質別)",
upper = list(continuous = wrap("cor", size = 3)), # 上半分は相関係数を表示
lower = list(continuous = wrap("points", size = 1.5)), # 下半分は散布図を表示
diag = list(continuous = wrap("densityDiag", alpha = 0.5)) # 対角線は密度プロットを表示
) +
scale_fill_manual(values = c("高品質" = "#F8766D", "標準品質" = "#00BFC4")) +
scale_shape_manual(values = c("高品質" = 1, "標準品質" = 2)) +
theme_bw() +
theme(strip.text = element_text(size = 10))
print(p_pairs)
# ランダムフォレストモデルを500本の決定木で学習させます
# importance=TRUE にして特徴量の重要度を計算させる
rf_model <- randomForest(quality ~ ., data = tomato_data, ntree = 500, importance = TRUE)
# モデルの概要を出力
print(rf_model)
Call:
randomForest(formula = quality ~ ., data = tomato_data, ntree = 500, importance = TRUE)
Type of random forest: classification
Number of trees: 500
No. of variables tried at each split: 2
OOB estimate of error rate: 2.2%
Confusion matrix:
高品質 標準品質 class.error
高品質 244 6 0.024
標準品質 5 245 0.020Figure 1 読み方
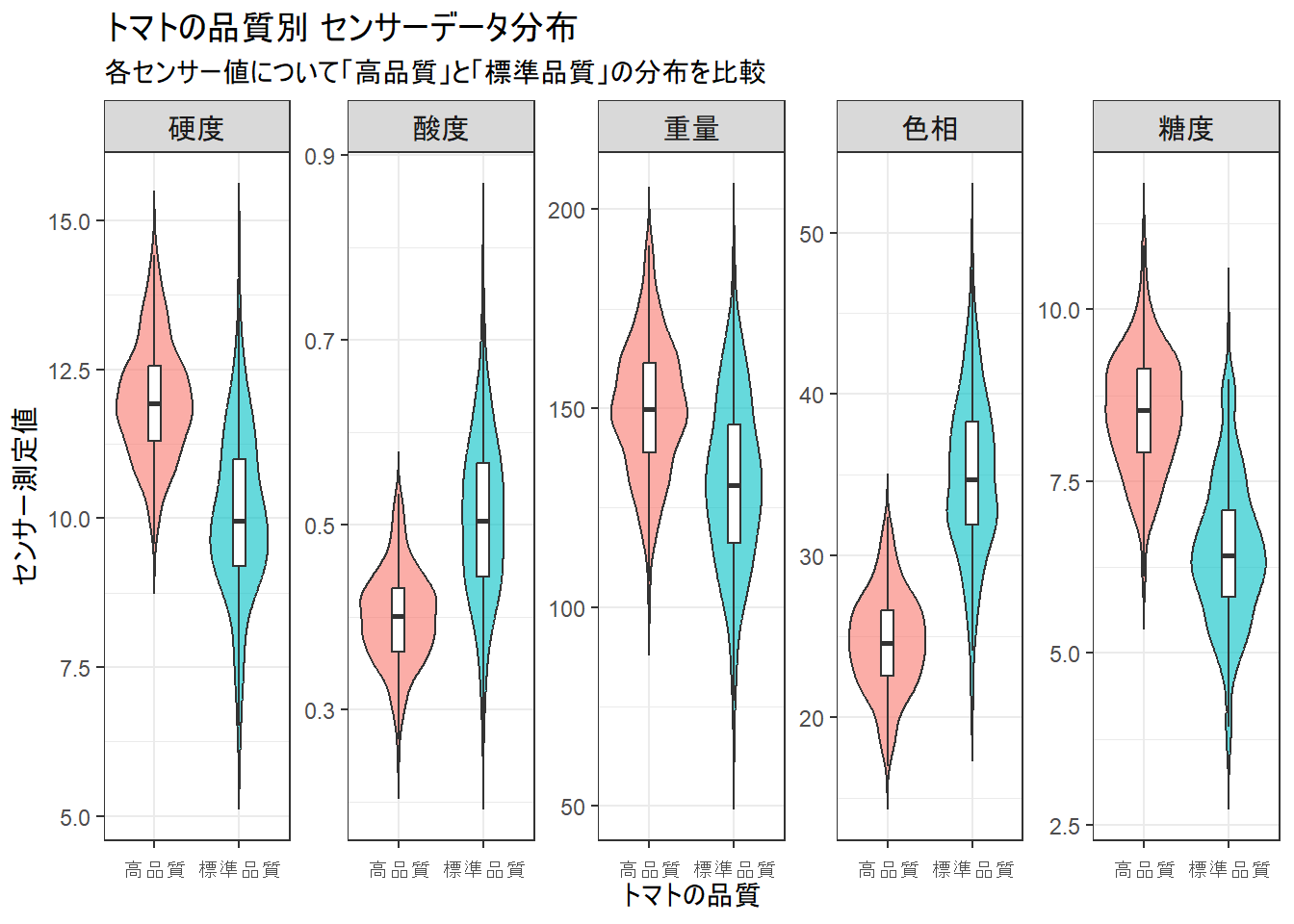
Figure 1 は、高品質トマトと標準品質トマトで、各センサーの値がどのように違うかを示したものです。
例えば一番左の『硬度』のグラフを見ると、高品質トマト(赤色)は全体的に標準品質トマト(青色)よりも高い値に分布していることが分かります。
同様に『重量』や『糖度』も高品質トマトの方が高い傾向にあります。
一方で、『酸度』や『色相』は高品質トマトの方が低い値を示す傾向があります。
両グループで分布がはっきりと分かれている特徴量ほど、品質を見分ける上で重要な指標であると言えます。
Figure 2 の読み方
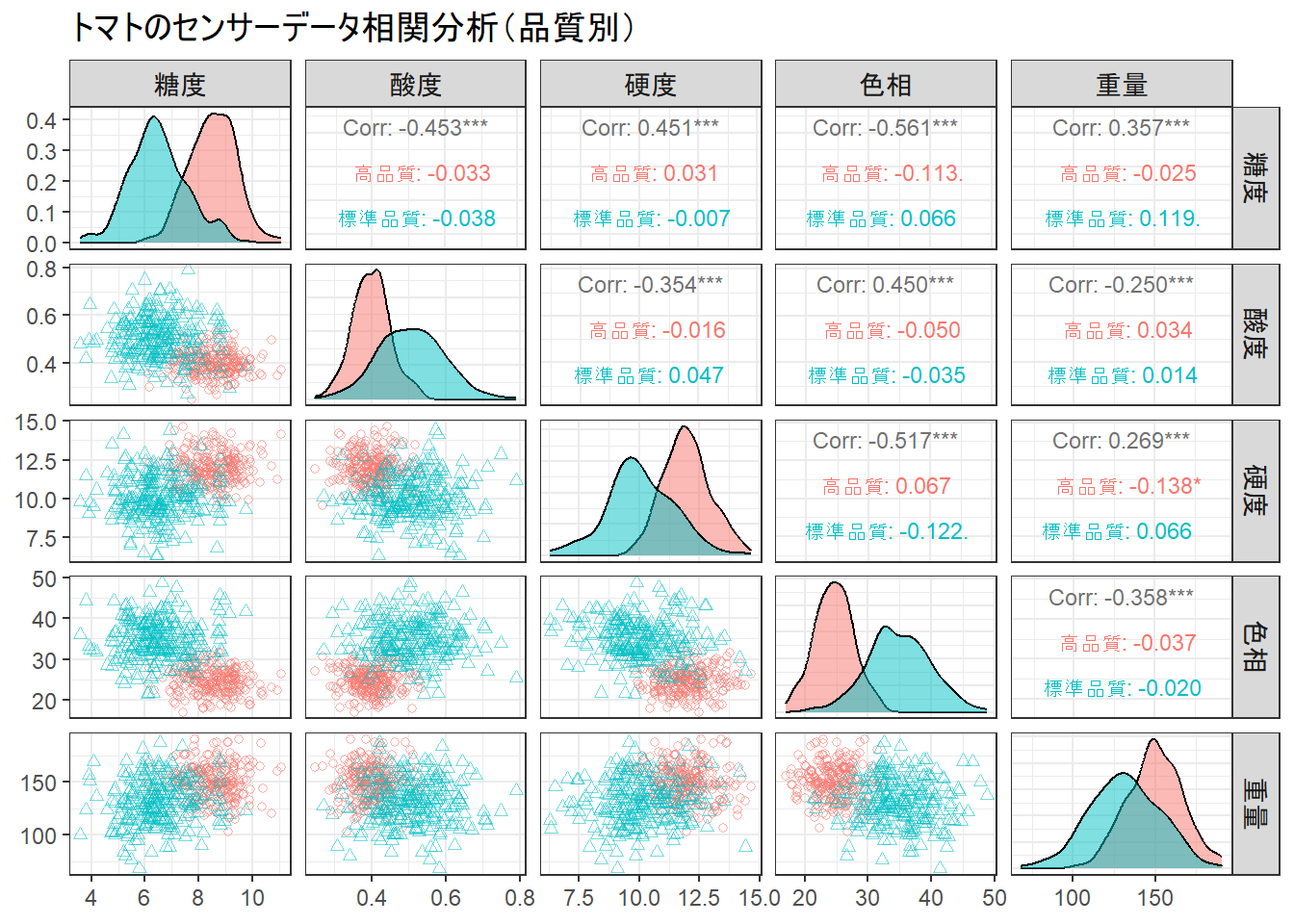
Figure 2 は、5つのセンサーデータそれぞれを他の4つのデータと比較したものです。データ全体の傾向を俯瞰的に捉えることができます。
まず、対角線上のグラフ(『糖度』と『糖度』が交差するマスなど)は、各センサー値の分布を示しています。
先ほどのバイオリンプロットと同様に、高品質(赤)と標準品質(青)で分布が異なることがわかります。
左下のエリアは散布図です。例えば、『糖度』(横軸)と『色相』(縦軸)のマスを見ると、2つのグループが比較的きれいに分かれていることがわかります。これは、この2つの特徴量を組み合わせると品質を判別しやすいことを意味します。
右上のエリアは相関係数です。絶対値が大きいほど強い関係があることを示します。
出力結果の説明
-
Type of random forest: classification:- 「分類」モデルであることを意味します。これは、目的変数(
quality)が「高品質」、「標準品質」のようなカテゴリカルなデータであるためです。もし目的変数が数値(例:トマトの糖度そのもの)であれば、regression(回帰)と表示されます。
- 「分類」モデルであることを意味します。これは、目的変数(
-
No. of variables tried at each split: 2:- 決定木の各ノード(分岐点)で分割ルールを決定する際に、候補としてランダムに選ばれた説明変数の数を示します。このモデルでは、5つの特徴量(糖度、酸度、硬度、色相、重量)の中から、毎回ランダムに2つだけを選び出し、その2つの中で最もデータをうまく分割できるルールを探す、という処理が繰り返されたことを意味します。通常、分類問題の場合は全特徴量の数の平方根(√5 ≒ 2.23 なので、デフォルトで2)が自動的に設定されます。
-
OOB estimate of error rate: 2.2%:- OOB(Out-of-Bag)データによる推定誤分類率です。これは、このモデルの汎化性能(未知のデータに対する予測精度)を測るための指標です。
- ランダムフォレストは、学習データを復元抽出し(ブートストラップサンプリング)、複数のデータセットを作って個々の木を学習させます。このとき、各データセットには元のデータの一部しか含まれません。あるデータ(例:トマトA)の視点から見ると、自分を学習データに含んでいない木が森の中に多数存在します。
- この「自分を学習に使わなかった木々」だけを使ってトマトAの品質を予測させ、実際の品質と合っているかをテストします。これを全てのデータに対して行い、間違えた割合を計算したものがOOB誤差率です。
-
2.2%ということは、このモデルは学習データに全く含まれていなかった未知のデータに対しても、約97.8%の正解率が期待できる、ということを示唆しています。
-
Confusion matrix::- 混同行列です。これもOOBデータを使って計算されており、モデルがどのクラスをどのクラスに間違えやすいかを示しています。
- 行: 実際のクラス(正解)
- 列: モデルの予測結果
-
高品質行: 実際に「高品質」だった250個のトマトのうち、-
244個は正しく「高品質」と予測された。 -
6個は誤って「標準品質」と予測された。
-
-
標準品質行: 実際に「標準品質」だった250個のトマトのうち、-
5個は誤って「高品質」と予測された。 -
245個は正しく「標準品質」と予測された。
-
-
class.error列: 各クラスごとの誤分類率です。- 高品質クラスの誤分類率:
6 / (244 + 6) = 6 / 250 = 0.024 (2.4%) - 標準品質クラスの誤分類率:
5 / (5 + 245) = 5 / 250 = 0.020 (2.0%)
- 高品質クラスの誤分類率:
- 全体のOOB誤差率は、全ての誤分類の合計を全データ数で割ったものになります:
(6 + 5) / (250 + 250) = 11 / 500 = 0.022 (2.2%)。これは上記のOOB estimate of error rateの値と一致します。
ステップ2:特徴量の重要度の可視化
# どの特徴量がトマトの品質判定に重要だったかを可視化します
# 特徴量の重要度データを取得
importance_data <- as.data.frame(importance(rf_model))
importance_data$feature <- rownames(importance_data)
# 日本語の特徴量名を追加
importance_data$feature_jp <- factor(c("糖度", "酸度", "硬度", "色相", "重量"))
# MeanDecreaseGini(ジニ不純度の減少量平均)を使ってプロット
p_importance <- ggplot(importance_data, aes(x = reorder(feature_jp, MeanDecreaseGini), y = MeanDecreaseGini)) +
geom_col(fill = "skyblue", color = "black") +
coord_flip() + # 横向きの棒グラフにする
labs(
title = "特徴量の重要度(トマトの品質判定)",
subtitle = "値が大きいほど、品質の分類に大きく貢献した特徴量であることを示す",
x = "特徴量",
y = "重要度 (Mean Decrease Gini)"
) +
theme_bw()
print(p_importance)Figure 3 の読み方
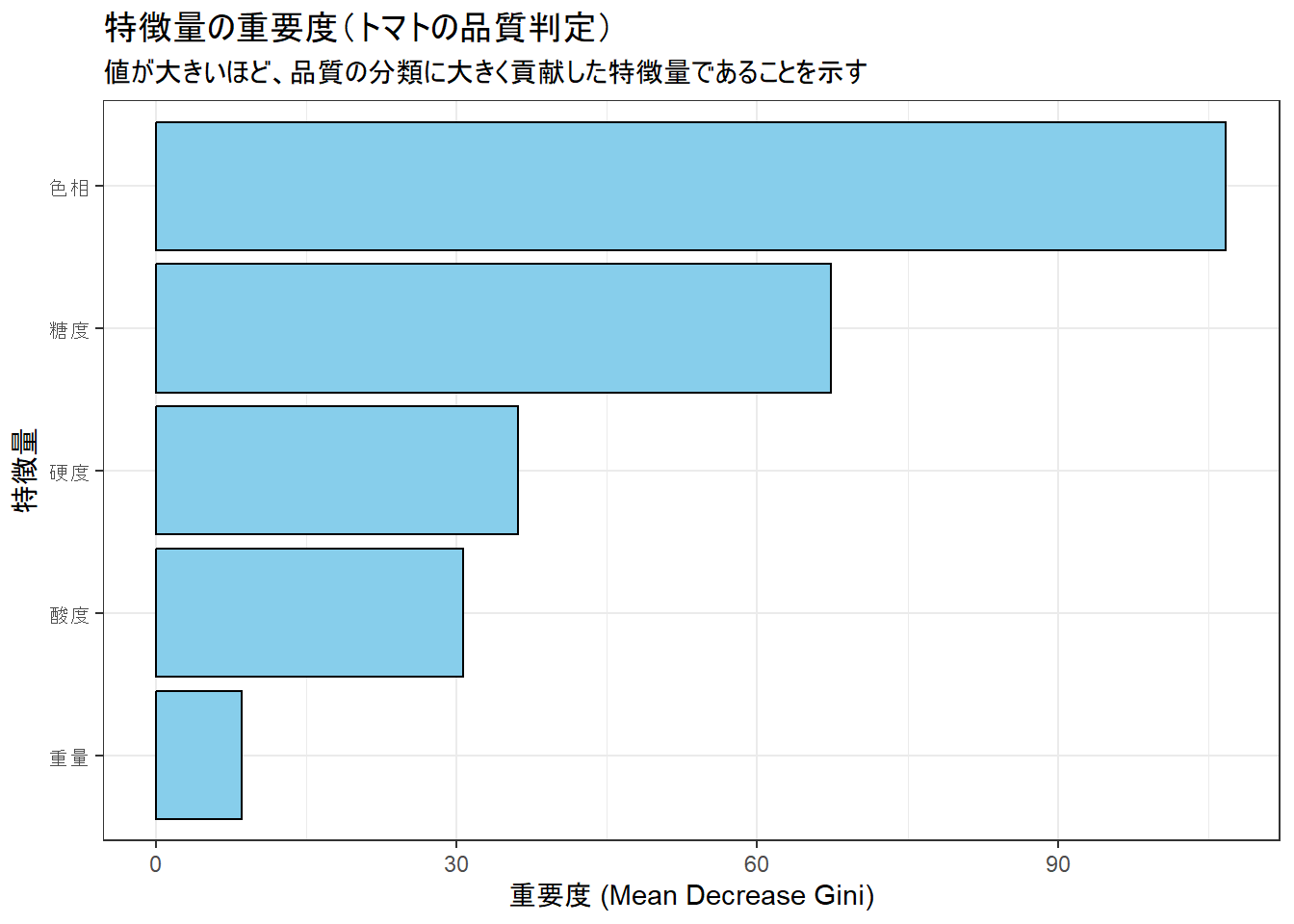
- Figure 3 は、各特徴量がモデルの予測精度向上にどれだけ貢献したかを示しています。
- 今回は「色相」が最も重要な特徴量であり、次いで「糖度」、「硬度」、「酸度」、「重量」の順になっていることがわかります。
- この結果から、高品質なトマトを生産するためには、特に色、そして糖度を管理することが重要であるという知見が得られます。
ステップ3:OOB誤差率の収束過程の確認
# 決定木の数を増やしていくとOOB誤差率がどのように変化するか確認します
# OOB誤差率のデータを抽出してデータフレームに変換
oob_error_data <- as.data.frame(rf_model$err.rate)
oob_error_data$num_trees <- 1:nrow(oob_error_data)
# データをプロットしやすい形式(ロング形式)に変換
oob_error_long <- oob_error_data %>%
pivot_longer(cols = -num_trees, names_to = "error_type", values_to = "error_rate") %>%
mutate(error_type_jp = case_when(
error_type == "OOB" ~ "全体 (OOB)",
error_type == "高品質" ~ "高品質クラス",
error_type == "標準品質" ~ "標準品質クラス"
))
# OOB誤差率の推移をプロット
p_oob <- ggplot(oob_error_long, aes(x = num_trees, y = error_rate, color = error_type_jp)) +
geom_line(linewidth = 1) +
labs(
title = "決定木の数とOOB誤差率の関係",
subtitle = "木の数が増えるにつれて誤差率が収束し、モデルが安定していく様子",
x = "決定木の数",
y = "OOB誤差率",
color = "誤差の種類"
) +
scale_y_continuous(labels = scales::percent_format()) + # y軸をパーセント表示に
theme_bw() +
theme(legend.position = "bottom")
print(p_oob)Figure 4 の読み方
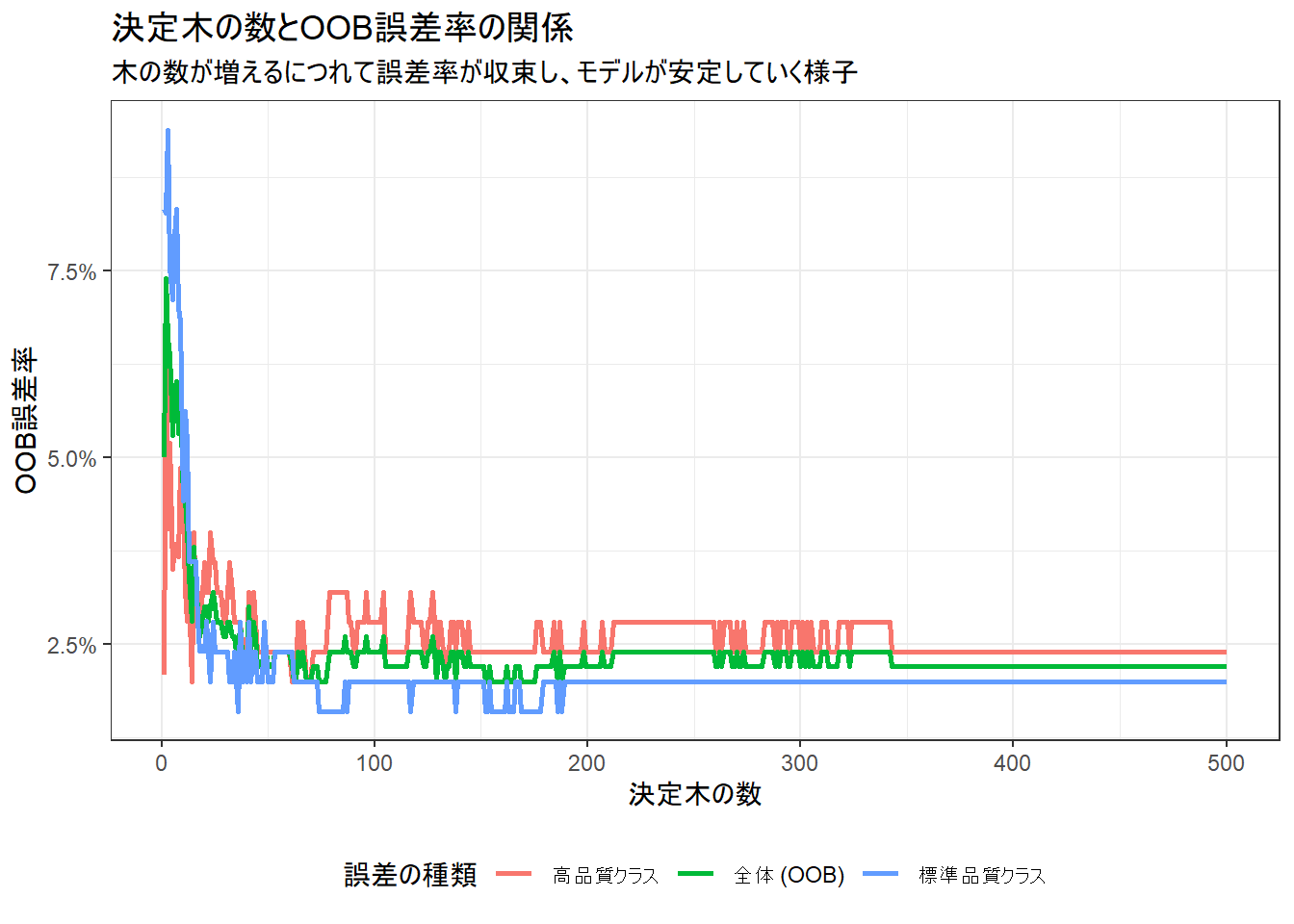
- 横軸が森を構成する決定木の数、縦軸がOOB誤差率です。
- 木の数が少ないうちは誤差率の変動が激しいですが、数が増えるにつれて(今回は100本程度で)誤差率が安定した値に収束していくのがわかります。
- これは、多くの多様な木の意見を集約することで、モデル全体として安定し、過学習が抑制されていることを示唆しています。
以上です。