Rで機械学習:勾配ブースティング(回帰)

基本的なアイデア：間違いから学ぶ専門家チーム

勾配ブースティングの仕組みは、「間違いを修正しながら学習を進める専門家チーム」に例えることができます。

1. 最初の専門家（1本目の木）:
   • まず、非常にシンプルなモデル（通常は決定木、特に深さの浅い「弱学習器」）が、全てのデータに対して大雑把な予測を行います。当然、この予測には多くの誤差（間違い）が含まれます。
2. 2人目の専門家（2本目の木）:
   • 次に、2人目の専門家が登場します。この専門家は、元のデータを予測するのではなく、1人目の専門家が犯した「間違い」そのものを予測するように学習します。
3. チームの予測を更新:
   • 最初の専門家の予測に、2人目の専門家が予測した「間違いの修正分」を少しだけ加えます。これにより、チーム全体の予測は、最初の予測よりも少しだけ正解に近づきます。
4. 3人目以降の専門家:
   • 3人目の専門家は、更新された「チーム全体の予測」が依然として犯している残りの間違いを予測するように学習します。
   • そして、その修正分をさらにチームの予測に少しだけ加えます。
5. 繰り返し:
   • この「現在のチームの間違いを、新しい専門家が学習して修正する」というプロセスを、指定された回数（例えば100回）繰り返します。

最終的に、この多数の専門家（決定木）の予測を足し合わせたものが、勾配ブースティングモデルの最終的な予測となります。

「勾配」の意味

「勾配」という言葉は、この「間違いを修正する」プロセスが、損失関数（モデルの予測がどれだけ悪いかを示す指標）の勾配（最も急な坂）を下る方向に行われていることに由来します。各ステップで、モデルは損失が最も減少する方向に予測を少しずつ修正していきます。

重要なハイパーパラメータ

• 木の数 (n.trees): チームに何人の専門家（決定木）を加えるか。多すぎると過学習のリスクがあります。
• 学習率 (learning rate / shrinkage): 新しい専門家の修正分を、どれくらいの重みでチームの予測に加えるか。小さい値（例: 0.01-0.1）にすると、一歩一歩慎重に学習が進み、過学習を防ぐ効果があります。
• 木の深さ (max_depth): 個々の専門家（決定木）がどれだけ複雑なルールを持てるか。通常は浅い木（例: 深さ4-8）が使われます。

準備：必要なライブラリの読み込み

# ライブラリの読み込み
library(xgboost)
library(caret)
library(dplyr)

シミュレーションの実行と定量的評価

• 勾配ブースティングによりシェアサイクルの需要を予測します。
• 天候データなど5つの特徴量から、1日のレンタル数を予測します。
• データは訓練用(80%)とテスト用(20%)に分割します。

# 再現性のための乱数シード設定
seed <- 20250817
set.seed(seed)

# データ生成
n_days <- 500
bike_data <- data.frame(
  temperature = runif(n_days, 5, 35),
  humidity = runif(n_days, 30, 90),
  wind_speed = runif(n_days, 2, 12),
  is_weekend = factor(sample(c("はい", "いいえ"), n_days, replace = TRUE, prob = c(2 / 7, 5 / 7))),
  is_holiday = factor(sample(c("はい", "いいえ"), n_days, replace = TRUE, prob = c(0.05, 0.95)))
)

# レンタル数を、特徴量との関係性＋ノイズで生成
bike_data <- bike_data %>%
  mutate(
    rentals = 200 +
      (temperature - 20) * 30 - # 気温20度が基準
      (humidity - 60) * 5 - # 湿度60%が基準
      (wind_speed - 7) * 20 + # 風速7m/sが基準
      ifelse(is_weekend == "はい", 300, 0) +
      ifelse(is_holiday == "はい", 400, 0) +
      rnorm(n_days, 0, 150) # ノイズ
  ) %>%
  # 負のレンタル数は0に補正
  mutate(rentals = pmax(0, rentals))

# 1. データを訓練用とテスト用に分割
train_indices <- createDataPartition(bike_data$rentals, p = 0.8, list = FALSE)
train_data <- bike_data[train_indices, ]
test_data <- bike_data[-train_indices, ]

# 2. クロスバリデーションの設定
# 訓練データ内で最適なハイパーパラメータを見つけるために10分割交差検証を行う
cv_control <- trainControl(method = "cv", number = 10)

# 3. チューニングするハイパーパラメータのグリッドを作成
xgb_grid <- expand.grid(
  nrounds = c(50, 100), # 木の数
  max_depth = c(3, 6), # 木の深さ
  eta = c(0.1, 0.3), # 学習率
  gamma = 0, # これらは固定
  colsample_bytree = 0.8, # これらは固定
  min_child_weight = 1, # これらは固定
  subsample = 0.8 # これらは固定
)


# 4. モデルの学習とチューニング
# caret::train関数が、CVとグリッドサーチを実行
# ハイパーパラメータの全組み合わせ（2 * 2 * 2 = 8通り）について、
# それぞれ10分割交差検証
xgb_model <- train(
  rentals ~ .,
  data = train_data,
  method = "xgbTree",
  trControl = cv_control,
  tuneGrid = xgb_grid,
  verbosity = 0 # 途中のログ出力を抑制
)

cat("--- 評価結果 ---\n")
# CVでの各パラメータの性能と、最も良かったパラメータを表示
cat("■ クロスバリデーションによるチューニング結果:\n")
print(xgb_model)

cat("\n■ 最適なハイパーパラメータ:\n")
print(xgb_model$bestTune)

# 5. 最終的なモデル性能の評価
cat("\n■ テストデータによる最終性能評価:\n")
cat("チューニングで得られた最適なモデルを、未知のテストデータに適用し、その性能を評価します。\n")

# テストデータで予測
predictions <- predict(xgb_model, test_data)

# 性能指標を計算
final_performance <- postResample(pred = predictions, obs = test_data$rentals)
print(final_performance)

--- 評価結果 ---
■ クロスバリデーションによるチューニング結果:
eXtreme Gradient Boosting 

400 samples
  5 predictor

No pre-processing
Resampling: Cross-Validated (10 fold) 
Summary of sample sizes: 360, 360, 360, 360, 360, 360, ... 
Resampling results across tuning parameters:

  eta  max_depth  nrounds  RMSE      Rsquared   MAE     
  0.1  3           50      140.1622  0.8140762  103.3082
  0.1  3          100      139.7122  0.8133012  103.5700
  0.1  6           50      153.3769  0.7752598  113.5181
  0.1  6          100      155.8635  0.7665298  116.6074
  0.3  3           50      146.4849  0.7934220  109.7146
  0.3  3          100      154.2157  0.7721010  115.9992
  0.3  6           50      164.8853  0.7391187  126.4735
  0.3  6          100      165.9841  0.7354237  127.1377

Tuning parameter 'gamma' was held constant at a value of 0
Tuning

Tuning parameter 'min_child_weight' was held constant at a value of 1

Tuning parameter 'subsample' was held constant at a value of 0.8
RMSE was used to select the optimal model using the smallest value.
The final values used for the model were nrounds = 100, max_depth = 3, eta
 = 0.1, gamma = 0, colsample_bytree = 0.8, min_child_weight = 1 and subsample
 = 0.8.

■ 最適なハイパーパラメータ:
  nrounds max_depth eta gamma colsample_bytree min_child_weight subsample
2     100         3 0.1     0              0.8                1       0.8

■ テストデータによる最終性能評価:
チューニングで得られた最適なモデルを、未知のテストデータに適用し、その性能を評価します。
      RMSE   Rsquared        MAE 
155.445663   0.748766 114.914836 

■ 評価指標の解説:

• RMSE (Root Mean Squared Error): 予測誤差の平均的な大きさを示します。計算過程で誤差を二乗するため、大きな誤差（外れ値）の影響を強く受けやすい特徴があります。値が小さいほど、予測精度が高いことを意味します。（単位はレンタル数）
• Rsquared (R-squared, 決定係数): モデルがデータの変動をどれだけうまく説明できているかを示す指標（0-1）。1に近いほど、モデルがデータによく適合していることを意味します。今回の結果(約0.75)は、レンタル数の変動の約75%をこのモデルで説明できている(5つの特徴量（気温、湿度、風速、週末、祝日）で説明できている)ことを示しています。
• MAE (Mean Absolute Error): 予測誤差の絶対値の平均です。RMSEと異なり、誤差を二乗しないため、外れ値の影響を受けにくく、予測誤差の大きさをより直感的に理解しやすいという利点があります。この結果(約115)は、『このモデルの予測は、平均するとおよそ115台くらい実際の数とズレる』、例えば、モデルが「明日は1000台レンタルされる」と予測した場合、実際の結果はだいたい 1000 ± 115 の範囲（885台から1115台）に収まることが多い、と解釈できます。

# 6. 特徴量の重要度を可視化
plot(varImp(xgb_model))

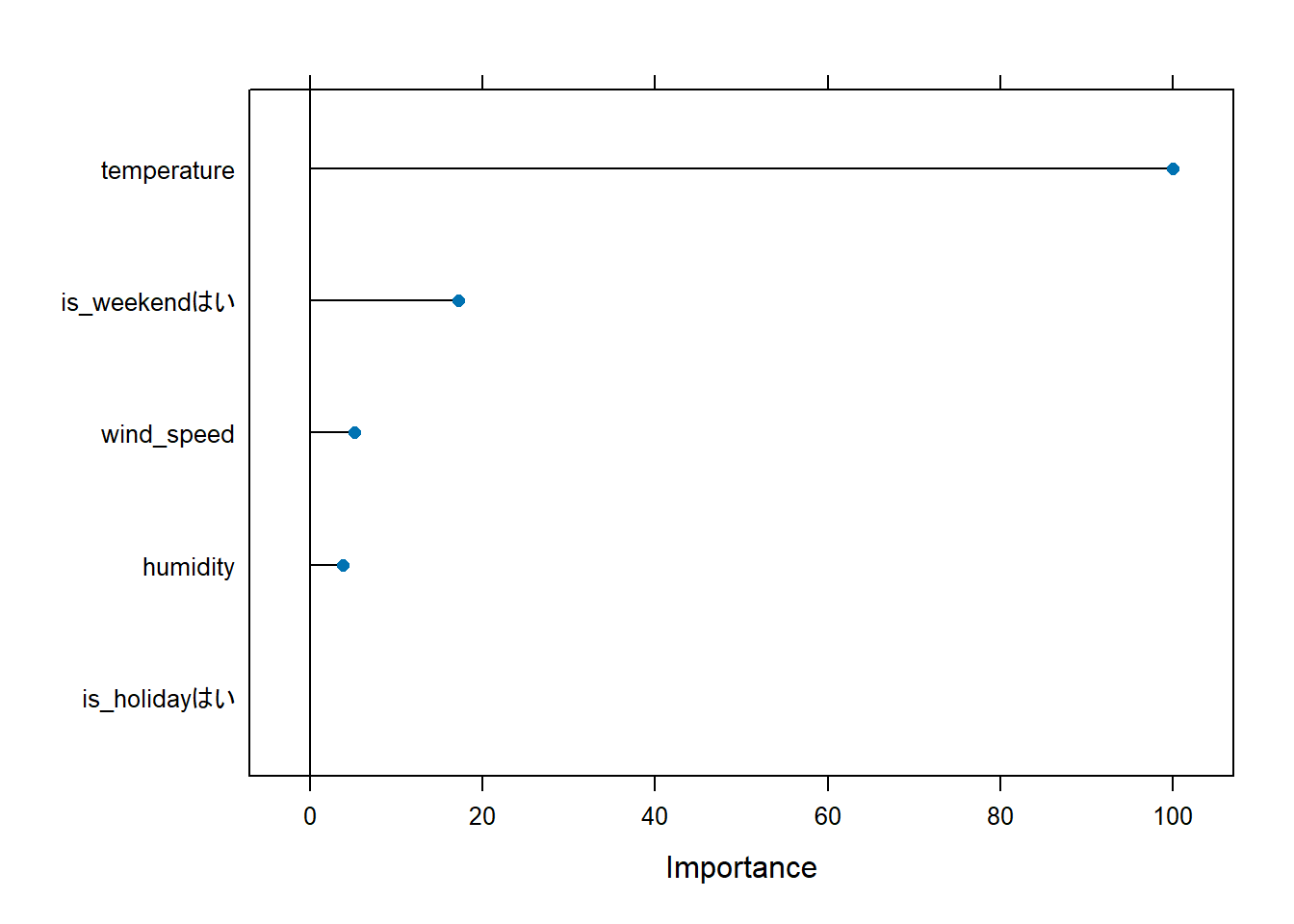
■ Figure 1 の解説

Figure 1 は、構築された勾配ブースティングモデルが、どの特徴量を「重要」と判断してレンタル数を予測したかを可視化したものです。横軸のImportance（重要度）は、最も重要な特徴量を100とした場合の相対的なスコアを示しています。

1. temperature (気温): 重要度が100となっており、圧倒的に最も重要な特徴量であることがわかります。これは「気温が快適かどうか」が、人々が自転車に乗るかどうかを決定する最大の要因であることを、モデルがデータから学習したことを示しています。
2. is_weekendはい (週末かどうか): 2番目に重要な特徴量です。is_weekendは「はい」と「いいえ」の2つの値を取りますが、ここでは特に「はい」の場合（つまり週末であること）が予測に大きく貢献したことを示しています。平日の利用パターンと週末のレジャー利用パターンが明確に異なり、その区別が予測精度向上に大きく寄与したことがわかります。
3. wind_speed (風速) と humidity (湿度): 3番目、4番目に重要な特徴量として続いています。気温ほどではありませんが、風の強さや湿度の高さも、サイクリングの快適さを左右する要因として、モデルが無視できない重要性を持つと判断したことが読み取れます。
4. is_holidayはい (祝日かどうか): 最も重要度が低い特徴量となっています。これは、今回のデータセットにおいては「祝日であること」が、他の要因（特に気温や週末かどうか）ほどレンタル数に一貫した影響を与えなかったことを示唆しています。

以上です。