Rで 機械学習:勾配ブースティング(分類) を試みます。
本ポストはこちらの続きです。

1. 分類における勾配ブースティング
勾配ブースティングの基本的な考え方(間違いから逐次的に学ぶ専門家チーム)は、回帰も分類も同じです。しかし、「間違い」の定義が異なります。
- 回帰の場合: 「間違い」は、予測値と実際の数値との差(残差)でした。
- 分類の場合: 「間違い」は、各クラスに属する確率の予測が、実際のクラス(0か1か)からどれだけズレているか(対数尤度の勾配など)で測られます。
アルゴリズムは、この確率の予測誤差を最も減少させる方向に、次の決定木を学習させていきます。最終的に、全ての木の予測を統合し、「このデータはクラスAに属する確率が85%」といった形で、確率として予測結果を出力します。
2. シミュレーションのシナリオ
舞台: 大手通信キャリアの顧客維持戦略チーム
あなたは、この通信キャリアのデータ分析官です。近年、顧客の解約(チャーン)率の上昇が問題となっており、経営陣から「解約しそうな顧客を事前に予測し、解約を防ぐための対策を打ちたい」という特命が下されました。
あなたのミッションは、顧客の契約情報や利用状況のデータから、その顧客が翌月に解約するかどうかを予測する高精度な分類モデルを、勾配ブースティングで構築することです。
予測に使用する特徴量(5つ):
-
tenure(契約期間 月数): 契約期間が短いほど解約しやすい傾向がある。 -
monthly_charges(月額料金): 料金が高いほど、不満による解約のリスクが高まる。 -
technical_support_calls(テクニカルサポートへの電話回数): 頻繁に電話している顧客は、何らかの問題を抱えている可能性が高い。 -
contract_type(契約タイプ): 「月契約」、「1年契約」、「2年契約」の3種類。月契約の顧客が最も解約しやすい。 -
has_streaming_tv: 付加サービスである「ストリーミングTV」を契約しているか (はい/いいえ)。複数サービス契約者は解約しにくい傾向がある。
目的変数:
-
churn: 翌月に解約したか (はい/いいえ)
3. R言語によるシミュレーションコード
分類タスクにおける、モデルの評価指標とする混同行列(Confusion Matrix)やROC曲線下の面積(AUC)などを caretパッケージにより求めます。
準備:必要なライブラリの読み込み
# ライブラリの読み込み
library(xgboost)
library(caret)
library(dplyr)シミュレーションの実行と定量的評価
- 5つの顧客情報から、翌月の解約を予測します。
# 再現性のための乱数シード設定
seed <- 20250817
set.seed(seed)
# データ生成
n_customers <- 1000
# 解約する顧客のデータ (リスクが高いプロファイル)
churn_yes <- data.frame(
tenure = rpois(200, lambda = 8),
monthly_charges = rnorm(200, mean = 90, sd = 15),
technical_support_calls = rpois(200, lambda = 3),
contract_type = factor(sample(c("月契約", "1年契約", "2年契約"), 200, replace = TRUE, prob = c(0.8, 0.15, 0.05))),
has_streaming_tv = factor(sample(c("はい", "いいえ"), 200, replace = TRUE, prob = c(0.4, 0.6))),
churn = "はい"
)
# 継続する顧客のデータ (リスクが低いプロファイル)
churn_no <- data.frame(
tenure = rpois(800, lambda = 40),
monthly_charges = rnorm(800, mean = 65, sd = 20),
technical_support_calls = rpois(800, lambda = 0.8),
contract_type = factor(sample(c("月契約", "1年契約", "2年契約"), 800, replace = TRUE, prob = c(0.3, 0.4, 0.3))),
has_streaming_tv = factor(sample(c("はい", "いいえ"), 800, replace = TRUE, prob = c(0.6, 0.4))),
churn = "いいえ"
)
customer_data <- rbind(churn_yes, churn_no)
customer_data$churn <- factor(customer_data$churn, levels = c("はい", "いいえ")) # 「はい」を陽性クラスに
# 1. データを訓練用とテスト用に分割
# データを訓練用(80%)とテスト用(20%)に分割します。
train_indices <- createDataPartition(customer_data$churn, p = 0.8, list = FALSE)
train_data <- customer_data[train_indices, ]
test_data <- customer_data[-train_indices, ]
# 2. クロスバリデーションの設定
# 分類タスクでは、ROCなどを計算するためsummaryFunctionとclassProbsを設定
cv_control <- trainControl(
method = "cv", number = 10,
summaryFunction = twoClassSummary,
classProbs = TRUE
)
# 3. チューニングするハイパーパラメータのグリッドを作成
xgb_grid_class <- expand.grid(
nrounds = c(50, 100),
max_depth = 6,
eta = 0.1,
gamma = 0,
colsample_bytree = 0.8,
min_child_weight = 1,
subsample = 0.8
)
# 4. モデルの学習とチューニング
# 評価指標(metric)として、クラスの不均衡に強い"ROC"を指定
xgb_model_class <- train(
churn ~ .,
data = train_data,
method = "xgbTree",
trControl = cv_control,
tuneGrid = xgb_grid_class,
metric = "ROC",
verbosity = 0
)
cat("--- 定量的な評価結果 ---\n")
cat("■ クロスバリデーションによるチューニング結果:\n")
print(xgb_model_class)
# 5. 最終的なモデル性能の評価
cat("\n■ テストデータによる最終性能評価:\n")
cat("チューニングで得られた最適なモデルを、未知のテストデータに適用し、その性能を評価します。\n")
predictions_class <- predict(xgb_model_class, test_data)
# 混同行列(Confusion Matrix)で性能を評価
# positive="はい"で、「はい」を正しく予測できたかを基準に評価
conf_matrix <- confusionMatrix(predictions_class, test_data$churn, positive = "はい")
print(conf_matrix)--- 定量的な評価結果 ---
■ クロスバリデーションによるチューニング結果:
eXtreme Gradient Boosting
800 samples
5 predictor
2 classes: 'はい', 'いいえ'
No pre-processing
Resampling: Cross-Validated (10 fold)
Summary of sample sizes: 720, 720, 720, 720, 720, 720, ...
Resampling results across tuning parameters:
nrounds ROC Sens Spec
50 0.9997559 1 0.9984375
100 0.9997559 1 0.9984375
Tuning parameter 'max_depth' was held constant at a value of 6
Tuning
parameter 'min_child_weight' was held constant at a value of 1
Tuning parameter 'subsample' was held constant at a value of 0.8
ROC was used to select the optimal model using the largest value.
The final values used for the model were nrounds = 50, max_depth = 6, eta
= 0.1, gamma = 0, colsample_bytree = 0.8, min_child_weight = 1 and subsample
= 0.8.
■ テストデータによる最終性能評価:
チューニングで得られた最適なモデルを、未知のテストデータに適用し、その性能を評価します。
Confusion Matrix and Statistics
Reference
Prediction はい いいえ
はい 40 0
いいえ 0 160
Accuracy : 1
95% CI : (0.9817, 1)
No Information Rate : 0.8
P-Value [Acc > NIR] : < 2.2e-16
Kappa : 1
Mcnemar's Test P-Value : NA
Sensitivity : 1.0
Specificity : 1.0
Pos Pred Value : 1.0
Neg Pred Value : 1.0
Prevalence : 0.2
Detection Rate : 0.2
Detection Prevalence : 0.2
Balanced Accuracy : 1.0
'Positive' Class : はい
■ チューニング結果の解説
print(xgb_model_class)の出力は、クロスバリデーションによる性能評価の結果を示しています。
-
ROCスコアが0.9997559: ROC曲線下の面積(AUC)は、モデルが解約する顧客としない顧客をどれだけうまく見分けられるかを示す指標で、1に近づくほど完璧なモデルを意味します。0.999という値は、モデルが両クラスをほぼ完璧に分離できていることを示しています。 -
Sens(感度) が1: 感度が1(100%)ということは、クロスバリデーションの過程で、実際に解約した顧客を一人も見逃さなかったことを意味します。 -
Spec(特異度) が0.998: 特異度が0.998(99.8%)ということは、解約しなかった顧客を誤って「解約しそう」と判断する間違いが、0.2%であったことを示しています。
これらの結果から、nrounds=50(木の数=50本)の時点で、すでに極めて高い性能に達していることがわかります。
■ 最終性能評価の解説
print(conf_matrix)で表示された混同行列は、未知のテストデータに対する最終的な答え合わせの結果です。
Reference
Prediction はい いいえ
はい 40 0
いいえ 0 160-
Accuracy : 1(正解率100%): テストデータ200人(解約者40人、継続者160人)全員を、一人も間違えることなく完璧に予測しました。 -
Sensitivity : 1.0: 実際に解約した40人のうち、全員(100%)を正しく「解約する」と予測できました。(解約者の見逃しゼロ) -
Specificity : 1.0: 実際には解約しなかった160人のうち、全員(100%)を正しく「解約しない」と予測できました。(優良顧客への誤った警告ゼロ)
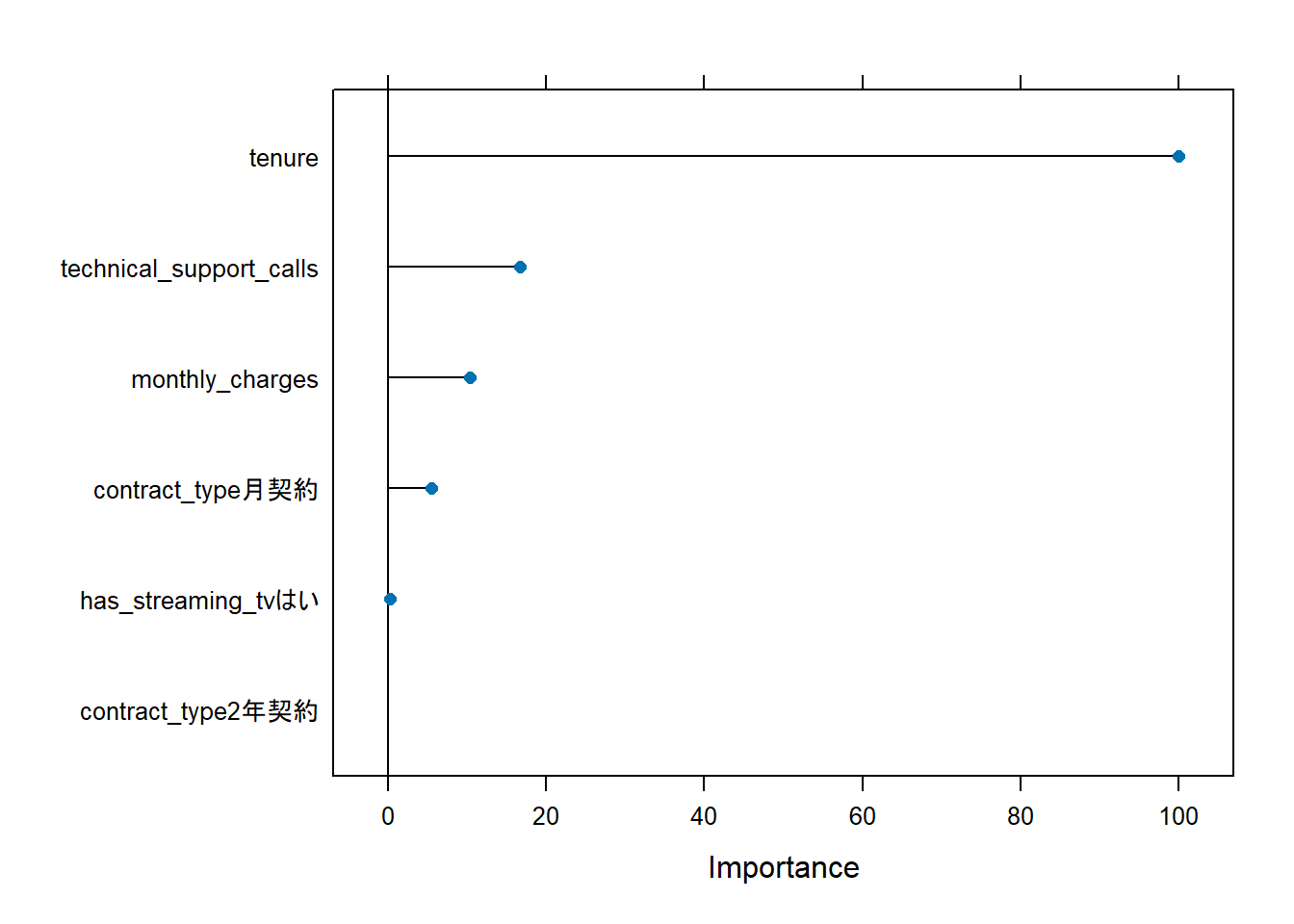
■ Figure 1 の解説
plot(varImp(xgb_model_class))の Figure 1 は、tenure (契約期間) が 圧倒的に最も重要な特徴量であることを示唆しており、顧客がどのくらいの期間サービスを契約しているかが、解約を予測する上で最大の鍵であることがわかります。
短期契約者と長期契約者とで、解約率に大きな差があること(差を付けたサンプルとしていること)をモデルは学習したと考えられます。
以上です。