Rで 機械学習:決定木 を試みます。
本ポストはこちらの続きです。

Rで機械学習:サポートベクターマシン
const typesetMath = (el) => { if (window.MathJax) { // MathJax Typeset window.MathJax.typeset(); } else if (window.katex...
1. 決定木(Decision Tree)とは
決定木は、その名の通り、木のような構造を用いて分類や回帰の問題を解く教師あり学習アルゴリズムです。特に分類問題でよく用いられ、そのモデルは人間にとって理解しやすいという特徴があります。
決定木の仕組み
決定木は、データを繰り返し分割していくことで予測モデルを構築します。その構造は以下の要素からなります。
- ノード(Node): 木の分岐点。各ノードでは、ある一つの特徴量に関する「質問」(例:「糖度は14以上か?」)が行われます。
- ブランチ(Branch): 質問に対する答え(例:「はい」または「いいえ」)によって分かれる経路。
- リーフ(Leaf): 木の末端。これ以上分割されないノードで、データの最終的な分類クラス(例:「フジリンゴ」)が割り当てられます。
モデルの学習は、データを最もよく分割できる質問を各ステップで見つけ出すことによって進められます。この「分割の良さ」を測る指標として、主に以下の2つが使われます。
- 情報利得(Information Gain): 親ノードのエントロピー(不純度・乱雑さ)から、子ノードのエントロピーの加重平均を引いたもの。この値が大きいほど、分割によってデータの純度が高まった(うまく分類できた)ことを意味します。
- ジニ不純度(Gini Impurity): あるノード内のデータが、どれだけ異なるクラスで混ざり合っているかを示す指標。ジニ不純度が低いほど、ノードの純度が高い状態です。決定木は、このジニ不純度が最も減少するような質問を見つけ出します。
決定木の特徴
長所:
- 解釈性が高い: モデルが「もしAならばX、もしBならばY」という単純なif-thenルールの集まりとして表現されるため、なぜその予測結果になったのかを人間が直感的に理解できます。これは「ホワイトボックスモデル」とも呼ばれます。
- 前処理が少ない: データのスケール変換(標準化など)が基本的に不要です。
- 非線形な関係も捉えられる: データを矩形領域に分割していくため、複雑な非線形の関係性も表現できます。
短所:
- 過学習しやすい: 訓練データに過剰に適合しようとして、木を深くしすぎる傾向があります。その結果、少しノイズが入っただけのデータも厳密に分けようとして、未知のデータに対する予測性能(汎化性能)が低下することがあります。
- 不安定さ: 訓練データが少し変わるだけで、全く異なる構造の木が生成される可能性があります。
この過学習を防ぐため、木の深さを制限したり、分割に必要な最小サンプル数を設定したり、学習後に不要な枝を刈り込む剪定(Pruning)といったテクニックが用いられます。
2. シミュレーションのシナリオ
舞台: 前回に引き続き、とある果樹園
前回と同じく、あなたは「フジリンゴ」と「オウシュウナシ」を「糖度」と「硬度」から仕分けるシステムを開発しています。今回は、SVMではなく決定木を使って、誰にでも分かりやすい「仕分けルール」を作成することを目指します。
シナリオのステップ:
- 決定木の構築とルールの可視化:
- 果物の糖度・硬度データから、決定木モデルを学習させます。
- 学習した結果を「木構造の図」としてプロットし、どのようなif-thenルール(例:「糖度が13.5未満ならオウシュウナシ」)が生成されたかを確認します。
- このルールによって、特徴空間(糖度-硬度平面)がどのように矩形の領域に分割されるかを可視化し、決定木の挙動を直感的に理解します。
- 過学習(オーバーフィッティング)の体験:
- 決定木の学習に制限をかけずに、意図的に「過学習」したモデルを作成します。
- 過学習した木は、訓練データの一つ一つに細かく対応しようとするため、非常に複雑な木構造と、細切れにされた特徴空間になります。
- これにより、「なぜ決定木は過学習しやすいのか」とその対策の重要性を学びます。
3. R言語によるシミュレーションコード
それでは、シナリオに沿って決定木のシミュレーションを実行します。
準備:必要なライブラリの読み込み
# ライブラリの読み込み
library(rpart)
library(rpart.plot)
library(ggplot2)
library(dplyr)ステップ1:決定木の構築とルールの可視化
まず、適切なサイズの決定木を構築し、そのルールを可視化します。
# 再現性のための乱数シード設定
seed <- 20250810
set.seed(seed)
# データ生成 (SVMの時とほぼ同じだが、少し重なりを大きくする)
# フジリンゴとオウシュウナシの糖度・硬度データを生成します。
# 今回は、2つのクラスの分布に少し重なりがあるデータを使用します。
n <- 70 # 各クラスのデータ数
# フジリンゴのデータ
fuji_apple <- data.frame(
sugar = rnorm(n, mean = 14.5, sd = 1.8),
hardness = rnorm(n, mean = 7.5, sd = 1.2),
class = "フジリンゴ"
)
# オウシュウナシのデータ
oushu_pear <- data.frame(
sugar = rnorm(n, mean = 12.5, sd = 1.8),
hardness = rnorm(n, mean = 5.5, sd = 1.2),
class = "オウシュウナシ"
)
# データを結合
fruit_data_tree <- rbind(fuji_apple, oushu_pear)
fruit_data_tree$class <- as.factor(fruit_data_tree$class)
# 決定木モデルの学習
# cp(complexity parameter)は、モデルの複雑さを制御するパラメータ。
# 値が小さいほど木は深くなるが、ここではデフォルトに近い値で適切に剪定させる。
tree_model <- rpart(class ~ ., data = fruit_data_tree, method = "class", cp = 0.02)
# 決定木の構造をプロット
# extra=104: 各ノードにクラスごとのデータ数と確率を表示
# box.palette="auto": クラスごとにノードの色を自動設定
rpart.plot(tree_model,
type = 4,
extra = 104,
under = TRUE,
cex = 0.8,
box.palette = "auto",
main = "決定木による果物の分類ルール"
)
# 特徴空間の分割を可視化
# グリッドデータを作成
grid_range_tree <- apply(fruit_data_tree[, 1:2], 2, range)
x_grid_tree <- seq(from = grid_range_tree[1, 1], to = grid_range_tree[2, 1], length.out = 200)
y_grid_tree <- seq(from = grid_range_tree[1, 2], to = grid_range_tree[2, 2], length.out = 200)
grid_df_tree <- expand.grid(sugar = x_grid_tree, hardness = y_grid_tree)
# グリッドの各点で予測
grid_df_tree$predicted_class <- predict(tree_model, grid_df_tree, type = "class")
# プロットの作成
p_tree_space <- ggplot(data = fruit_data_tree, aes(x = sugar, y = hardness)) +
# 予測領域を背景色で描画
geom_raster(data = grid_df_tree, aes(fill = predicted_class), alpha = 0.3, interpolate = TRUE) +
# 元のデータをプロット
geom_point(aes(color = class, shape = class), size = 3) +
scale_color_manual(values = c("フジリンゴ" = "red", "オウシュウナシ" = "darkgreen")) +
scale_fill_manual(values = c("フジリンゴ" = "red", "オウシュウナシ" = "darkgreen")) +
scale_shape_manual(values = c("フジリンゴ" = 16, "オウシュウナシ" = 17)) +
guides(fill = "none") + # 背景色の凡例は非表示
labs(
title = "決定木による特徴空間の分割",
subtitle = "学習したルールによって、空間が矩形領域に分割されている",
x = "糖度",
y = "硬度",
color = "果物の種類",
shape = "果物の種類"
) +
theme_bw() +
theme(legend.position = "bottom")
print(p_tree_space)Figure 1 の説明:
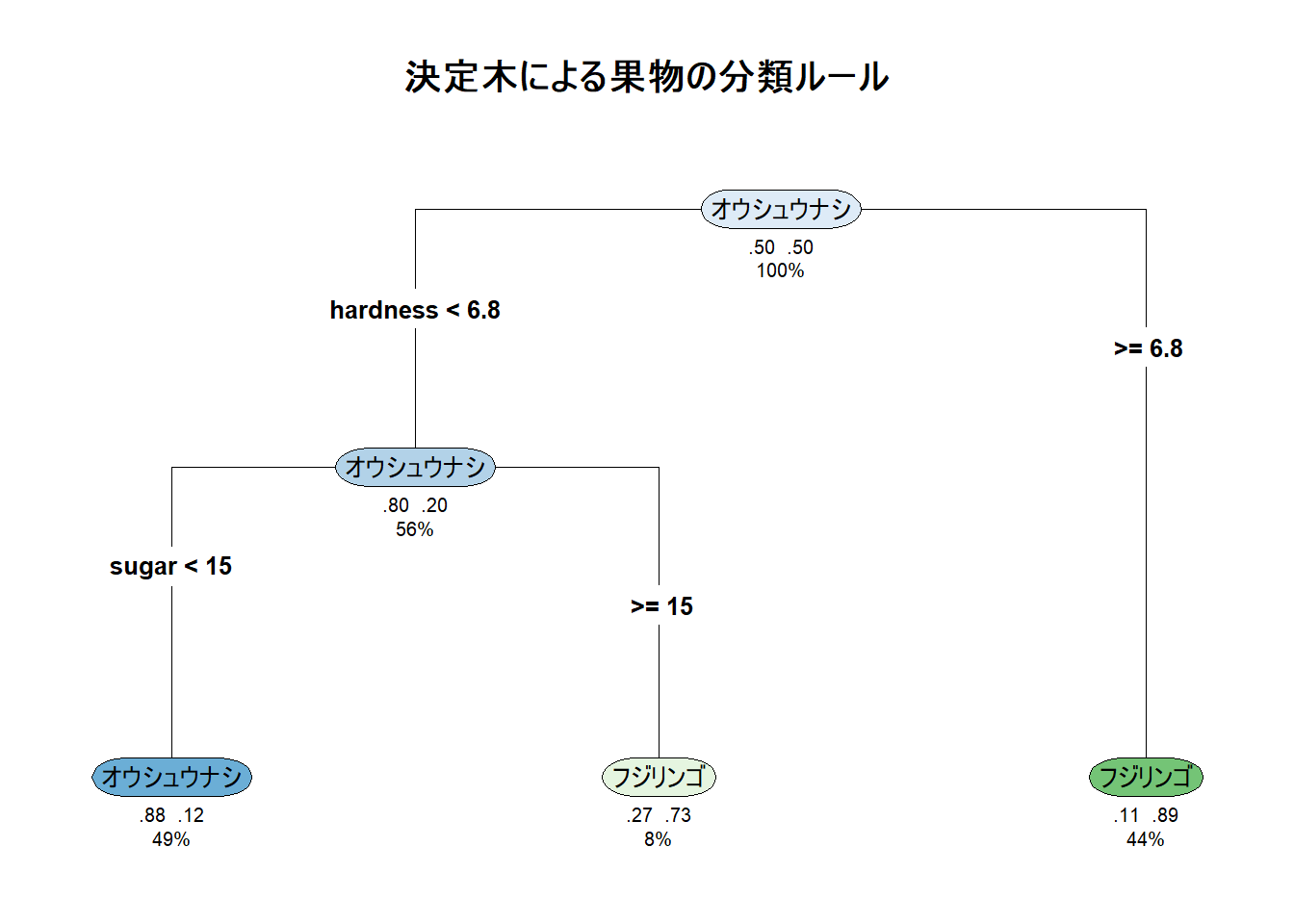
- 一番上のノード(ルートノード)から始まり、質問に答える形で下に分岐していきます。
- 各ノードには、分類の条件(例:hardness < 6.8, sugar < 15)、そのノードでの多数派クラス、クラスの確率、データ全体に占める割合が表示されています。
- この図を見るだけで、どのようなルールで果物が仕分けられるかが理解できます。
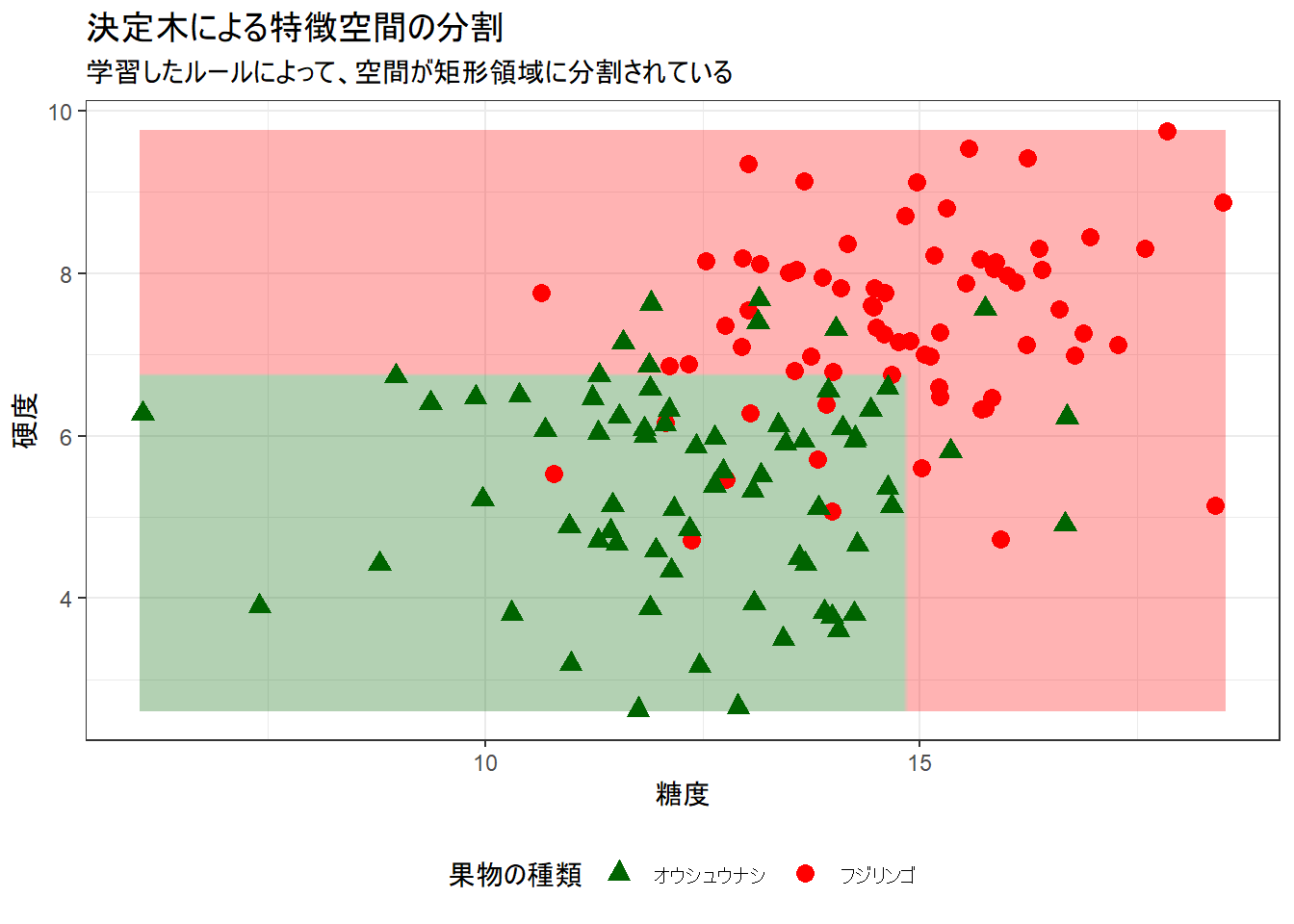
Figure 2 の説明:
- このプロットは、決定木のルールが糖度-硬度平面をどのように分割したかを示しています。
- 決定境界が、軸に平行な直線(矩形)で構成されていることがわかります。
ステップ2:過学習(オーバーフィッティング)の体験
次に、学習の制限を緩めて、意図的に過学習したモデルを作成します。
# 過学習した決定木モデル
# 決定木の学習パラメータを調整し、意図的に過学習したモデルを作成します。
# 具体的には、分割に必要な最小サンプル数を小さくし、cp値を0に近づけて剪定が行われないようにします。
# minsplit: ノードを分割するために必要な最小データ数
# cp: 0に設定すると、ごく僅かな改善でも分割を行うため、木が深くなる
overfit_tree_model <- rpart(class ~ .,
data = fruit_data_tree, method = "class",
control = rpart.control(minsplit = 2, cp = 0.0001)
)
# 過学習した木のプロット
rpart.plot(overfit_tree_model,
type = 4,
extra = 104,
under = TRUE,
cex = 0.6,
box.palette = "auto",
main = "過学習した決定木"
)
# 過学習モデルによる特徴空間の分割を可視化
grid_df_tree$predicted_class_overfit <- predict(overfit_tree_model, grid_df_tree, type = "class")
p_overfit_space <- ggplot(data = fruit_data_tree, aes(x = sugar, y = hardness)) +
geom_raster(data = grid_df_tree, aes(fill = predicted_class_overfit), alpha = 0.3, interpolate = TRUE) +
geom_point(aes(color = class, shape = class), size = 3) +
scale_color_manual(values = c("フジリンゴ" = "red", "オウシュウナシ" = "darkgreen")) +
scale_fill_manual(values = c("フジリンゴ" = "red", "オウシュウナシ" = "darkgreen")) +
scale_shape_manual(values = c("フジリンゴ" = 16, "オウシュウナシ" = 17)) +
guides(fill = "none") +
labs(
title = "過学習した決定木による特徴空間の分割",
subtitle = "訓練データの一つ一つを分類しようとして、空間が細かく分断されている",
x = "糖度",
y = "硬度",
color = "果物の種類",
shape = "果物の種類"
) +
theme_bw() +
theme(legend.position = "bottom")
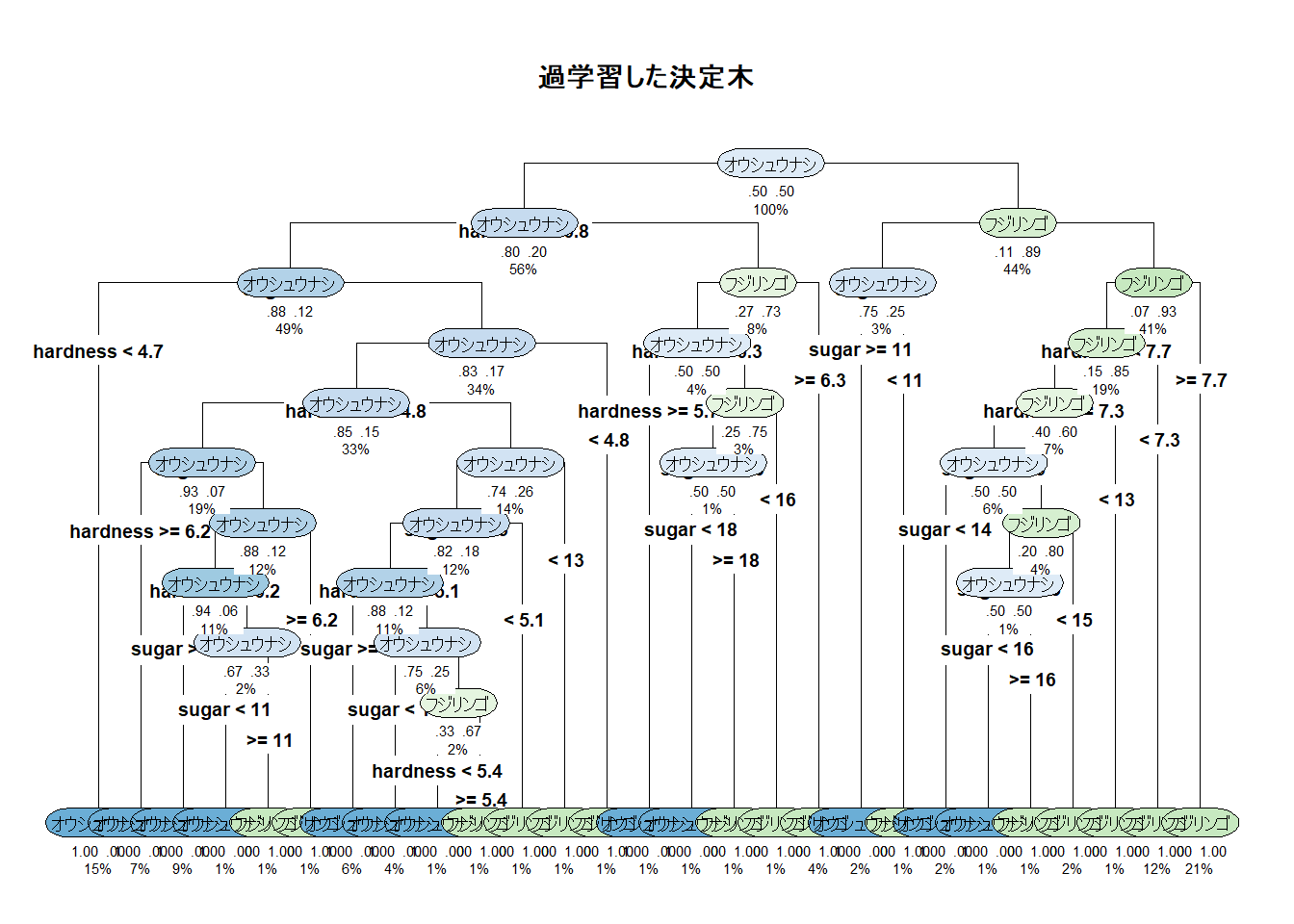
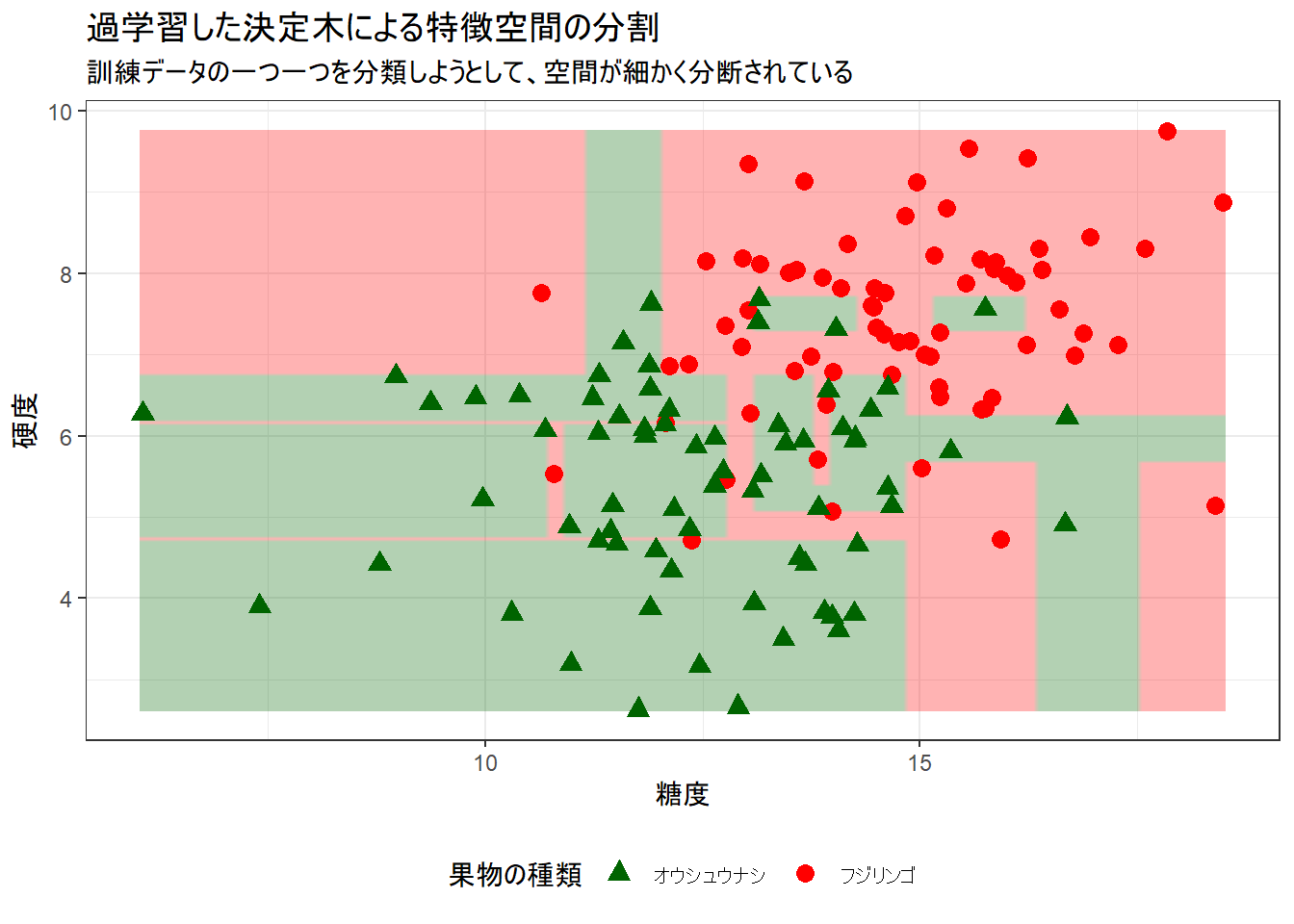
print(p_overfit_space)- 過学習したモデルでは、訓練データを完璧に分類しようとするあまり、非常に複雑なルールが生成されています。
- 特徴空間は、まるでモザイクアートのように細かく分割されています。これは「訓練データ」に対しては高い精度を出しますが、少しずれた「未知のデータ」が来た場合に、間違った分類をしてしまう可能性が高まります。
- この現象が「過学習」であり、これを防ぐために適切な剪定(pruning)やパラメータ調整が重要になります。
シミュレーションのまとめ
このシミュレーションでは、決定木がどのようにして分類ルールを学習し、それがどのように特徴空間の分割に対応するのかを確認しました。
- 解釈性の高さ: 学習したモデルは、人間が理解しやすい「if-thenルール」の木構造として表現され、なぜその予測になったのかを簡単に追跡できます。特徴空間は、そのルールに従って矩形に分割されます。
- 過学習のリスク: 決定木は、その柔軟さゆえに訓練データに過剰に適合しやすい性質を持ちます。パラメータを適切に制御しないと、汎化性能の低い、複雑すぎるモデルができてしまいます。
以上です。