Rで 相関係数:ケンドールの順位相関係数 を試みます。
本ポストはこちらの続きです。

1. ケンドールの順位相関係数とは
ケンドールの順位相関係数(Kendall’s Tau, \(\tau\))は、2つの変数の関係性を、ペアワイズでの順序の一致度に基づいて評価するノンパラメトリックな指標です。
データの中から任意の2つのペアを取り出し、その大小関係(順序)が2つの変数間で一致しているか(協和)、逆転しているか(不協和)を数え上げます。
- 協和ペア (Concordant Pair, C): 2つのデータペアの大小関係が、変数間で一致しているペア。
- 不協和ペア (Discordant Pair, D): 2つのデータペアの大小関係が、変数間で逆転しているペア。
データに同順位(タイ)がない場合、ケンドールのタウ(\(\tau_a\))は以下の式で計算されます。 \[ \tau_a = \dfrac{C - D}{C + D} = \dfrac{\text{協和ペア数} - \text{不協和ペア数}}{\text{総ペア数}} \] この指標は、データの値そのものではなく、順序のみに注目するため、外れ値(極端に大きな値や小さな値)の影響を受けにくい(頑健である)という特徴があります。
これに対し、ピアソンの積率相関係数は、データの値そのもの(平均からの距離)を用いて計算するため、外れ値が存在するとその値に大きく引きずられてしまい、データ全体の傾向を正しく表現できなくなることがあります。
2. シミュレーションに適したシナリオ
ピアソンとケンドールの違い、特に「外れ値への耐性」を明確にするため、以下のシナリオを設定します。
シナリオ:従業員の経験年数と生産性の関係
ある工場で、従業員の「勤続年数」と「1時間あたりの生産個数」の関係を調査しています。
- 変数X: 勤続年数
- 変数Y: 1時間あたりの生産個数
調査の結果、ほとんどの従業員は「勤続年数が長いほど、生産性も高い」という、綺麗な右上がりの直線的な関係にあることがわかりました。
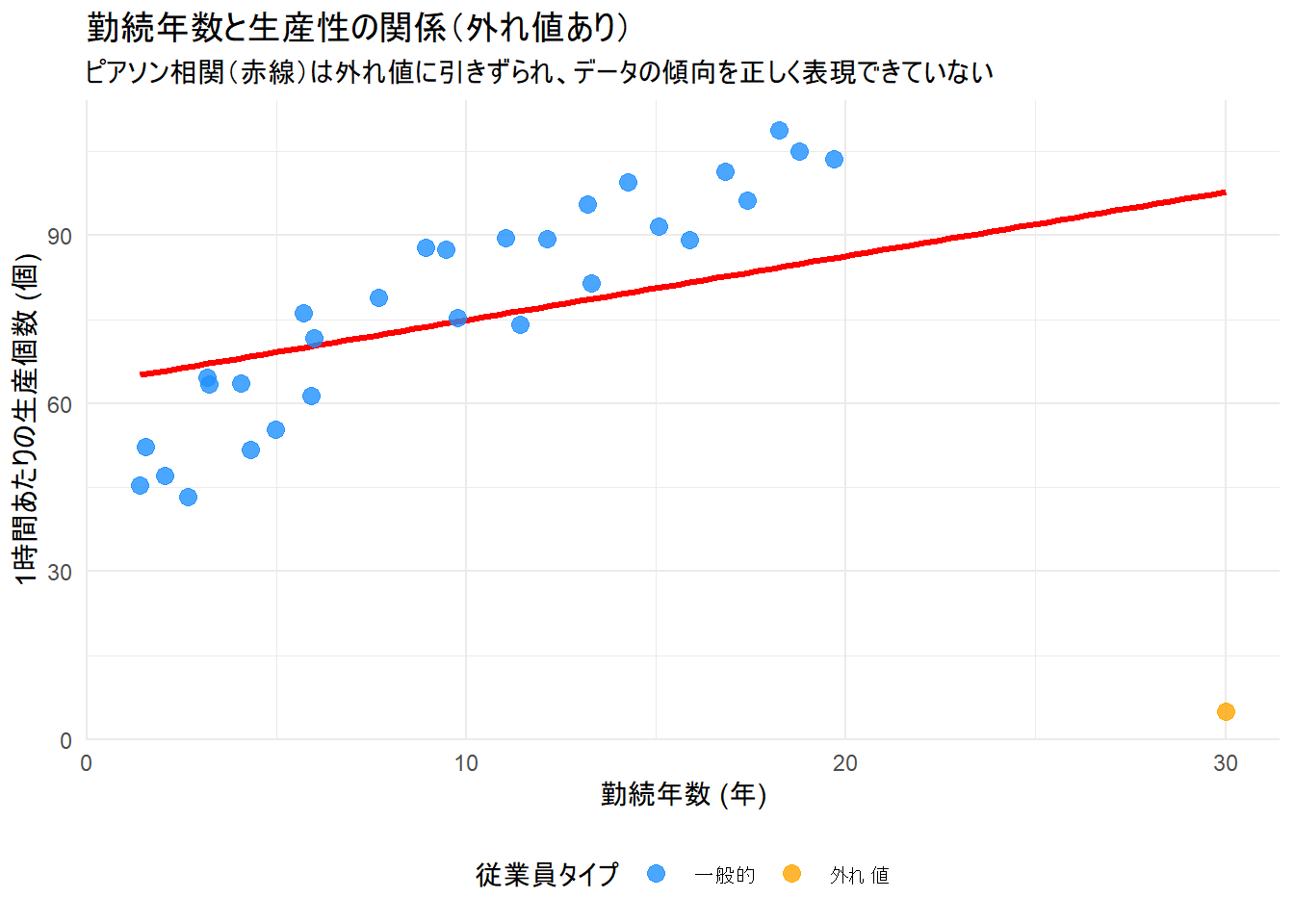
しかし、一人だけ例外的な従業員がいました。彼は勤続30年の大ベテランですが、何らかの理由で生産性が極端に低くなっています。このたった一人の外れ値が、相関関係の分析にどのような影響を与えるでしょうか?
- ピアソンの相関係数の予測: データの値そのものを使うため、この「勤続年数は最大なのに、生産性は最小」という外れ値データに強く引きずられ、全体の強い正の相関を過小評価してしまうはずです。
- ケンドールの順位相関係数の予測: データの順位を使うため、この外れ値の影響は限定的です。この従業員が関わるペアでは順序が逆転(不協和)しますが、他の大多数の従業員同士のペアでは順序が一致(協和)するため、データ全体の強い単調関係を頑健に捉えることができるはずです。
3. R言語によるシミュレーション
上記のシナリオに沿って、ピアソンとケンドールの相関係数およびp値を比較します。
# ライブラリの読み込み
library(ggplot2)
library(dplyr)
# 再現性のために乱数のシードを固定
seed <- 20250823
set.seed(seed)
# 1. データ生成
n_normal <- 29 # 一般的な従業員の数
n_outlier <- 1 # 外れ値の従業員の数
# n-1人の「一般的な」従業員データを生成
# 勤続年数と生産性の間に強い正の相関を持たせる
experience_normal <- runif(n_normal, 1, 20)
productivity_normal <- 50 + 3 * experience_normal + rnorm(n_normal, 0, 8)
# 1人の「外れ値」従業員データを生成
# 勤続年数は最長だが、生産性は極端に低い
experience_outlier <- 30
productivity_outlier <- 5
# データを結合
sim_data <- data.frame(
experience = c(experience_normal, experience_outlier),
productivity = c(productivity_normal, productivity_outlier),
type = c(rep("一般的", n_normal), "外れ値")
)
# 2. 相関係数とp値の計算と比較
# ピアソンの積率相関係数とp値の計算
pearson_test <- cor.test(sim_data$experience, sim_data$productivity, method = "pearson")
cat("--- ピアソンの検定結果 ---\n")
cat(paste0("相関係数 (r): ", round(pearson_test$estimate, 3), "\n"))
cat(paste0("p値: ", round(pearson_test$p.value, 3), "\n"))
# ケンドールの順位相関係数とp値の計算
kendall_test <- cor.test(sim_data$experience, sim_data$productivity, method = "kendall")
cat("--- ケンドールの検定結果 ---\n")
cat(paste0("相関係数 (τ): ", round(kendall_test$estimate, 3), "\n"))
cat(paste0("p値: ", format.pval(kendall_test$p.value, digits = 3, eps = 0.001), "\n"))
# 3. 可視化
g <- ggplot(sim_data, aes(x = experience, y = productivity)) +
# ピアソンが評価する直線(外れ値に大きく引きずられている)
geom_smooth(method = "lm", color = "red", se = FALSE, linewidth = 1.2, fullrange = TRUE) +
# 点をプロット(外れ値は色を変える)
geom_point(aes(color = type), size = 3, alpha = 0.8) +
scale_color_manual(name = "従業員タイプ", values = c("一般的" = "dodgerblue", "外れ値" = "orange")) +
labs(
title = "勤続年数と生産性の関係(外れ値あり)",
subtitle = "ピアソン相関(赤線)は外れ値に引きずられ、データの傾向を正しく表現できていない",
x = "勤続年数 (年)",
y = "1時間あたりの生産個数 (個)"
) +
theme_minimal() +
theme(legend.position = "bottom")
print(g)--- ピアソンの検定結果 ---
相関係数 (r): 0.333
p値: 0.072
--- ケンドールの検定結果 ---
相関係数 (τ): 0.651
p値: <0.001- ピアソンの相関検定では、たった一つの外れ値の影響で、相関係数は統計的に有意とは言えなくなっています(p > 0.05)。
- ケンドールの順位相関検定では、外れ値の影響を受けにくいため、依然として有意に正の相関を示しています。
4. スピアマンの順位相関とケンドールの順位相関の比較
スピアマンの順位相関係数(\(\rho_s\))とケンドールの順位相関係数(\(\tau\))は、どちらも2変数間の単調な関係(一方が増加すれば他方も増加/減少する傾向)を測定するための代表的なノンパラメトリック指標です。両者は外れ値に強く、非線形な関係も捉えることができるという共通点を持ちますが、その計算思想と特性において違いがあります。
1. 計算の基本思想の違い
スピアマン (\(\rho_s\)):順位の「距離」に基づく相関 スピアマンの相関係数は、各変数の値を順位に変換した後、その順位データに対してピアソンの積率相関係数を計算したものです。これは、2つの変数における「順位のズレ(距離)がどれくらい小さいか」を評価していると解釈できます。同順位がない場合の計算式は以下の通りです。 \[ \rho_s = 1 - \dfrac{6 \displaystyle\sum_{i=1}^{n} d_i^2}{n\left(n^2 - 1\right)} \] ここで、\(d_i\) は各データペアの順位の差です。この式が示すように、スピアマンは順位差の2乗 (\(d_i^2\)) に基づいており、順位が大きく離れているほど、相関係数を引き下げるペナルティが大きくなります。
ケンドール (\(\tau\)):ペアワイズでの「順序の一致」に基づく相関 ケンドールの相関係数は、データセットから取り出しうる全ての観測ペアについて、その順序関係を評価します。あるペアが一方の変数で
A > Bという順序なら、もう一方の変数でもA > Bとなっているか(協和)、それともA < Bとなっているか(不協和)を数え上げます。 \[ \tau = \dfrac{\text{協和ペアの数} - \text{不協和ペアの数}}{\text{総ペア数}} \] この指標は、ペアの順序が「一致しているか、していないか」の二値で判断します。順位が1つだけ違っていても、10違っていても、そのペアが不協和であることに変わりはなく、同じ「1カウント」として扱われます。つまり、順位差の大きさは考慮しません。
2. 感度と頑健性
この計算思想の違いは、外れ値やデータの乱れに対する感度の違いに繋がります。
| 特性 | スピアマンの \(\rho_s\) | ケンドールの \(\tau\) |
|---|---|---|
| 感度 | 順位の差の大きさに敏感。順位が大きくズレるデータ(例:1位と最下位の入れ替わり)があると、値が大きく変動する。 | 順位の差の大きさには鈍感。順序が逆転しているペアの数に敏感。一部の順位が大きくズレても、他の多くのペアの順序が一致していれば、値は比較的安定している。 |
| 頑健性 | 外れ値に強い。 | 外れ値に対して、スピアマンよりもさらに頑健であると言われる。これは、順位を大きく乱すような極端な外れ値の影響を、スピアマンほど受けないため。 |
3. 値の解釈と傾向
- 確率的な解釈: ケンドールの \(\tau\) は、「データからランダムに2つのペアを選んだ時、そのペアが協和である確率から、不協和である確率を引いた値」という、非常に直感的で明確な確率的解釈が可能です。スピアマンの \(\rho_s\) には、このような直接的な確率的解釈はありません。
- 値の大きさ: 同じデータセットに対して計算した場合、一般的にケンドールの \(\tau\) の絶対値は、スピアマンの \(\rho_s\) の絶対値よりも小さくなる傾向があります。ただし、これは常に成り立つわけではありません。
4. 相関係数の比較
ここでは、作成済みの sim_data を用い、以下の4つのケースで相関係数とp値を比較します。
- ピアソン(外れ値あり): 外れ値が分析に与える影響を確認します。
- ピアソン(外れ値なし): データの本質的な線形関係の強さ(基準値)を確認します。
- スピアマン(外れ値あり): 外れ値存在下での頑健性を評価します。
- ケンドール(外れ値あり): 外れ値存在下での頑健性を評価します。
# --- 4種類の相関係数とp値の比較 ---
cat("--- 4種類の相関係数とp値の比較 ---\n\n")
# 1. ピアソン(外れ値あり)
pearson_test_with_outlier <- cor.test(sim_data$experience, sim_data$productivity, method = "pearson")
cat("--- 1. ピアソン(外れ値あり) ---\n")
cat(paste0("相関係数 (r): ", round(pearson_test_with_outlier$estimate, 3), "\n"))
cat(paste0("p値: ", round(pearson_test_with_outlier$p.value, 3), "\n"))
# 外れ値を除いたデータセットを準備
sim_data_no_outlier <- sim_data %>% filter(type == "一般的")
# 2. ピアソン(外れ値なし)
pearson_test_no_outlier <- cor.test(sim_data_no_outlier$experience, sim_data_no_outlier$productivity, method = "pearson")
cat("--- 2. ピアソン(外れ値なし) ---\n")
cat(paste0("相関係数 (r): ", round(pearson_test_no_outlier$estimate, 3), "\n"))
cat(paste0("p値: ", format.pval(pearson_test_no_outlier$p.value, digits = 3, eps = 0.001), "\n"))
# 3. スピアマン(外れ値あり)
spearman_test <- cor.test(sim_data$experience, sim_data$productivity, method = "spearman", exact = FALSE)
cat("--- 3. スピアマン(外れ値あり) ---\n")
cat(paste0("相関係数 (ρs): ", round(spearman_test$estimate, 3), "\n"))
cat(paste0("p値: ", format.pval(spearman_test$p.value, digits = 3, eps = 0.001), "\n"))
# 4. ケンドール(外れ値あり)
kendall_test <- cor.test(sim_data$experience, sim_data$productivity, method = "kendall")
cat("--- 4. ケンドール(外れ値あり) ---\n")
cat(paste0("相関係数 (τ): ", round(kendall_test$estimate, 3), "\n"))
cat(paste0("p値: ", format.pval(kendall_test$p.value, digits = 3, eps = 0.001), "\n"))--- 4種類の相関係数とp値の比較 ---
--- 1. ピアソン(外れ値あり) ---
相関係数 (r): 0.333
p値: 0.072
--- 2. ピアソン(外れ値なし) ---
相関係数 (r): 0.93
p値: <0.001
--- 3. スピアマン(外れ値あり) ---
相関係数 (ρs): 0.745
p値: <0.001
--- 4. ケンドール(外れ値あり) ---
相関係数 (τ): 0.651
p値: <0.001まとめ
どちらの指標を選択するかは、分析者が「何を重視するか」によって決まります。
- スピアマンの \(\rho_s\) を選ぶ場合:
- 順位のズレが大きいことを、より大きなペナルティとして評価したい場合。
- ピアソンの相関係数のノンパラメトリック版として、広く一般的に使われている指標を用いたい場合。
- ケンドールの \(\tau\) を選ぶ場合:
- 順位差の大きさよりも、ペアの順序関係の一致度そのものを評価したい場合。
- 順位を大きく乱す可能性のある外れ値に対して、より頑健な指標を求める場合。
- 結果の確率的な解釈を重視する場合。
5. 「協和ペア」と「不協和ペア」の具体例
ここに、4人の従業員の「勤続年数」と「スキルスコア」のデータがあるとします。
| 従業員 | 勤続年数 (X) | スキルスコア (Y) |
|---|---|---|
| Aさん | 1年 | 60点 |
| Bさん | 3年 | 75点 |
| Cさん | 5年 | 70点 |
| Dさん | 8年 | 90点 |
この4人から、考えられる全てのペア(組み合わせ)を抜き出します。4人から2人を選ぶ組み合わせは6通りです。 (A, B), (A, C), (A, D), (B, C), (B, D), (C, D)
それでは、各ペアが「協和」か「不協和」かを一つずつ見ていきましょう。
1. ペア (Aさん, Bさん) の分析
- 勤続年数で比較: Aさん(1年) < Bさん(3年)
- スキルスコアで比較: Aさん(60点) < Bさん(75点)
両方の変数で「Aさん < Bさん」という順序関係が一致しています。 したがって、このペアは 協和 (Concordant) ペア です。
2. ペア (Aさん, Cさん) の分析
- 勤続年数で比較: Aさん(1年) < Cさん(5年)
- スキルスコアで比較: Aさん(60点) < Cさん(70点)
両方の変数で「Aさん < Cさん」という順序関係が一致しています。 したがって、このペアも 協和 (Concordant) ペア です。
3. ペア (Bさん, Cさん) の分析
- 勤続年数で比較: Bさん(3年) < Cさん(5年)
- スキルスコアで比較: Bさん(75点) > Cさん(70点)
勤続年数では「Bさん < Cさん」ですが、スキルスコアでは「Bさん > Cさん」と、順序関係が逆転しています。 したがって、このペアは 不協和 (Discordant) ペア です。
残りのペアも同様に分析します。
4. ペア (Aさん, Dさん): 勤続年数 A < D、スキルスコア A < D → 協和ペア
5. ペア (Bさん, Dさん): 勤続年数 B < D、スキルスコア B < D → 協和ペア
6. ペア (Cさん, Dさん): 勤続年数 C < D、スキルスコア C < D → 協和ペア
1. 結果の集計とケンドールのタウの計算
全てのペアを分析した結果、以下のことがわかりました。
- 協和ペア (C) の数: 5
- 不協和ペア (D) の数: 1
- 総ペア数: 6
これをケンドールのタウの公式に当てはめます。
\[ \tau = \dfrac{C - D}{C + D} = \dfrac{5 - 1}{5 + 1} = \dfrac{4}{6} \approx 0.667 \]
2. まとめ
この計算からわかるように、ケンドールの相関係数は、個々のデータの値の大きさ(例えば、BさんとCさんのスコアの差が5点であること)は一切考慮していません。
ただひたすらに、全てのペアについて「順序は同じ方向か?違う方向か?」という多数決を取っているのです。
今回の例では、6ペア中5ペアが同じ方向を向いており(協和)、1ペアだけが逆方向を向いていた(不協和)ため、全体として「強い正の相関がある」と結論付けられました。これがケンドールの順位相関係数の基本的な考え方です。
以上です。