Rで 相関係数:偏相関係数 を試みます。
1. 偏相関係数とは
偏相関係数(Partial Correlation Coefficient)とは、3つ以上の変数がある状況で、他の変数の影響を取り除いた後の2つの変数間の相関関係を示す指標です。
例えば、変数 \(X\), \(Y\), \(Z\) があるとします。このとき、\(Z\) の影響を統計的に統制(除去)した上での \(X\) と \(Y\) の間の相関を考えたい場合に偏相関係数を用います。これは、しばしば「見せかけの相関(疑似相関)」を特定するために利用されます。
変数 \(X\) と \(Y\) の相関係数を \(\rho_{XY}\)、変数 \(X\) と \(Z\) の相関係数を \(\rho_{XZ}\)、変数 \(Y\) と \(Z\) の相関係数を \(\rho_{YZ}\) とすると、\(Z\) の影響を取り除いた後の \(X\) と \(Y\) の偏相関係数 \(\rho_{XY \cdot Z}\) は、以下の式で計算されます。
\[
\rho_{XY \cdot Z} = \dfrac{\rho_{XY} - \rho_{XZ} \rho_{YZ}}{\sqrt{\left(1 - \rho_{XZ}^2\right)\left(1 - \rho_{YZ}^2\right)}}
\]
この式の意味を直感的に理解するには、線形回帰の「残差」を考えると分かりやすいです。
- 変数 \(X\) を変数 \(Z\) で説明する線形回帰を行い、その残差 \(e_{X \cdot Z}\) を求めます。この残差は、「\(Z\) では説明しきれなかった \(X\) の変動部分」を表します。
- 同様に、変数 \(Y\) を変数 \(Z\) で説明する線形回帰を行い、その残差 \(e_{Y \cdot Z}\) を求めます。この残差は、「\(Z\) では説明しきれなかった \(Y\) の変動部分」を表します。
- この2つの残差 \(e_{X \cdot Z}\) と \(e_{Y \cdot Z}\) の間の相関係数を計算すると、それが偏相関係数 \(\rho_{XY \cdot Z}\) となります。
つまり、偏相関係数は「互いの変数から第3の変数の影響を排除した、純粋な残り物同士の関係性」を測る指標と言えます。
2. シミュレーションに適したシナリオ
偏相関係数の概念を理解するために、典型的な「見せかけの相関」の例をシナリオとして設定します。
シナリオ:アイスクリームの売上と水難事故
ある町の統計データを分析したところ、以下の事実が判明しました。
- 変数X:アイスクリームの売上
- 変数Y:水難事故の発生件数
データを分析すると、「アイスクリームの売上が多い日ほど、水難事故の発生件数も多い」という強い正の相関が見られました。この結果だけを見ると、「アイスクリームの食べ過ぎが水難事故を引き起こすのでは?」という奇妙な結論に至るかもしれません。
しかし、ここには隠れた第3の変数が存在します。
- 変数Z:その日の最高気温
常識的に考えると、以下のような関係が推測されます。
- 気温が上がる(Z↑)と、人々は冷たいものを求めてアイスクリームを多く買う(X↑)。
- 気温が上がる(Z↑)と、人々は海や川へ涼みに行くため、結果として水難事故が増える(Y↑)。
つまり、アイスクリームの売上(X)と水難事故(Y)の間に直接的な因果関係はなく、共通の原因である「気温(Z)」によって、両者が同時に増減しているだけではないか、と推測できます。
この仮説を検証するために、「気温(Z)」の影響を取り除いたときの「アイスクリームの売上(X)」と「水難事故(Y)」の相関、すなわち偏相関係数を計算します。もし偏相関係数が0に近くなれば、当初見られた相関は「気温」による「見せかけの相関」であったと結論付けられます。
3. R言語によるシミュレーション
上記のシナリオに沿って、R言語でシミュレーションを行い、偏相関係数の効果を視覚的に確認します。
準備
まず、シミュレーションと可視化に必要なライブラリを読み込みます。偏相関係数の算出にはppcorを利用します。
# ライブラリの読み込み
library(ggplot2)
library(dplyr)
library(ppcor)シミュレーションコード
始めに単純な相関分析です。
# 再現性のために乱数のシードを固定
seed <- 20250822
set.seed(seed)
# データ数の設定
n <- 200
# 1. データ生成
# シナリオに基づいてデータを生成します
# 変数Z: 気温 (平均25度、標準偏差5度の正規分布に従うとする)
kion <- rnorm(n, mean = 25, sd = 5)
# 変数X: アイスクリームの売上
# 気温(kion)が高いほど売上が増えるように設定。
ice_uriage <- 50 * kion + rnorm(n, mean = 0, sd = 150)
# 変数Y: 水難事故の件数
# 気温(kion)が高いほど事故が増えるように設定。
jiko_kensu <- 1 * kion + rnorm(n, mean = 0, sd = 4)
# データをデータフレームにまとめる
sim_data <- data.frame(
ice_uriage = ice_uriage,
jiko_kensu = jiko_kensu,
kion = kion
)
# 2. 単純な相関分析
cat("--- 単純な相関分析 ---\n")
# アイスクリーム売上と水難事故件数の相関係数を計算
simple_cor <- cor(sim_data$ice_uriage, sim_data$jiko_kensu)
cat(paste0("アイスクリーム売上と水難事故件数の相関係数: ", round(simple_cor, 3), "\n"))
# 散布図で可視化
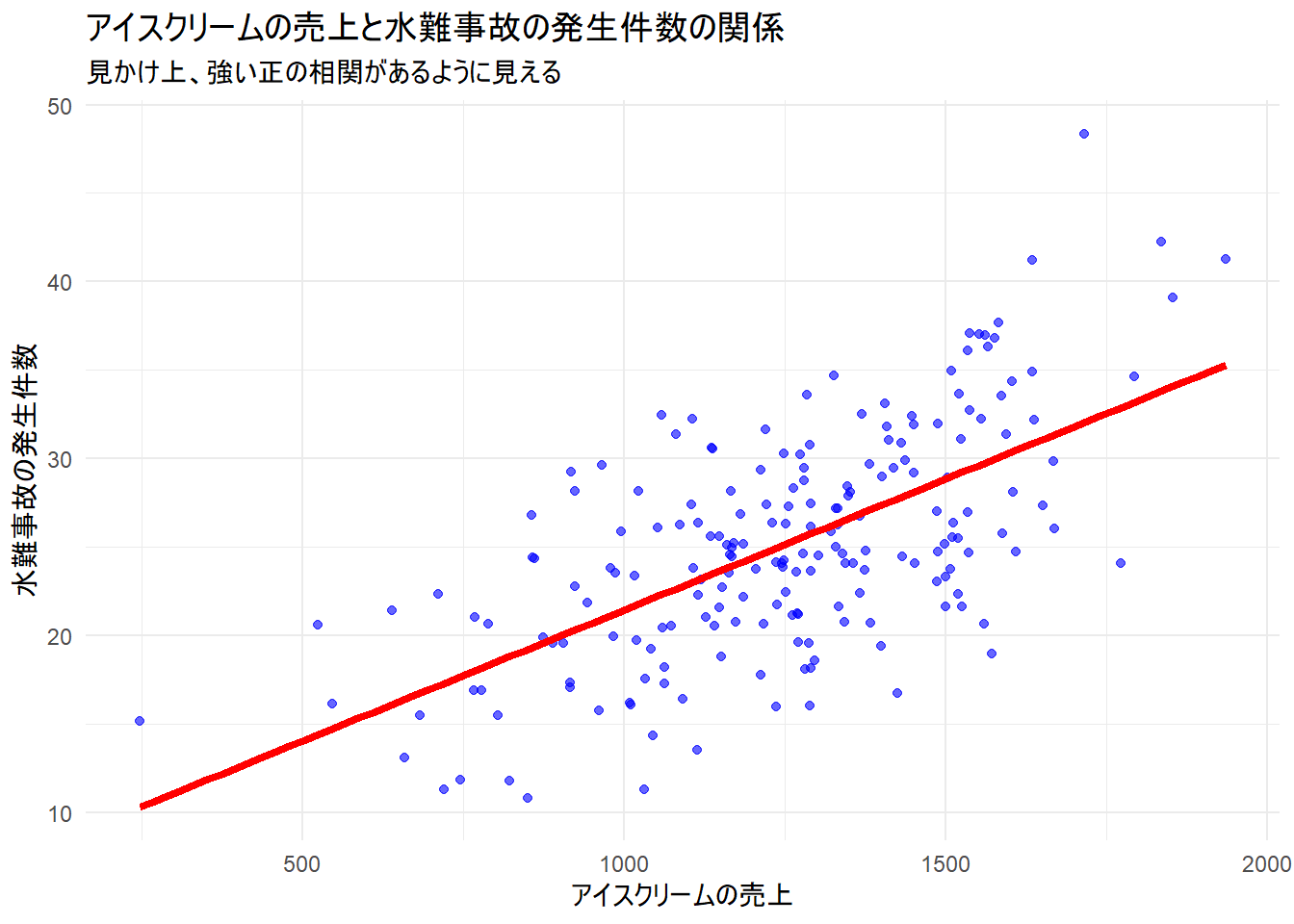
g1 <- ggplot(sim_data, aes(x = ice_uriage, y = jiko_kensu)) +
geom_point(alpha = 0.6, color = "blue") +
geom_smooth(method = "lm", se = FALSE, color = "red", linewidth = 1.5) +
labs(
title = "アイスクリームの売上と水難事故の発生件数の関係",
subtitle = "見かけ上、強い正の相関があるように見える",
x = "アイスクリームの売上",
y = "水難事故の発生件数"
) +
theme_minimal()
print(g1)--- 単純な相関分析 ---
アイスクリーム売上と水難事故件数の相関係数: 0.633アイスクリーム売上と水難事故件数には、強い正の相関が見られます。
続いて、偏相関分析を行います。
# 3. 偏相関分析
# 気温の影響を取り除いて、再度相関を分析します。
cat("--- 偏相関分析 ---\n")
# ppcorパッケージを使って偏相関係数を計算
partial_cor_result <- pcor.test(
sim_data$ice_uriage,
sim_data$jiko_kensu,
sim_data$kion
)
# 結果の表示
partial_cor <- partial_cor_result$estimate
p_value <- partial_cor_result$p.value
cat(paste0("気温の影響を除いた後の偏相関係数: ", round(partial_cor, 3), "\n"))
cat(paste0("p値: ", round(p_value, 3), "\n"))--- 偏相関分析 ---
気温の影響を除いた後の偏相関係数: -0.024
p値: 0.742偏相関係数はほぼ0になり、統計的に有意な相関はなくなりました。
このことから、当初見られた相関は「気温」という共通の原因による「見せかけの相関」であった可能性が高いと結論付けられます。
最後に、偏相関の概念を可視化(残差プロット)します。
偏相関は、各変数から気温の影響を取り除いた「残り物(残差)」同士の相関です。
# 4. 偏相関の概念を可視化(残差プロット)
# モデル1: アイスクリーム売上を気温で説明する
model_ice <- lm(ice_uriage ~ kion, data = sim_data)
# モデル2: 水難事故件数を気温で説明する
model_jiko <- lm(jiko_kensu ~ kion, data = sim_data)
# それぞれのモデルから残差(気温で説明できなかった部分)を抽出
sim_data <- sim_data %>%
mutate(
resid_ice = residuals(model_ice), # アイス売上の残差
resid_jiko = residuals(model_jiko) # 水難事故の残差
)
# 残差同士の相関係数を計算
resid_cor <- cor(sim_data$resid_ice, sim_data$resid_jiko)
cat("--- 残差同士の相関分析 ---\n")
cat(paste0("残差同士の相関係数: ", round(resid_cor, 3), "\n"))
# 残差の散布図を作成
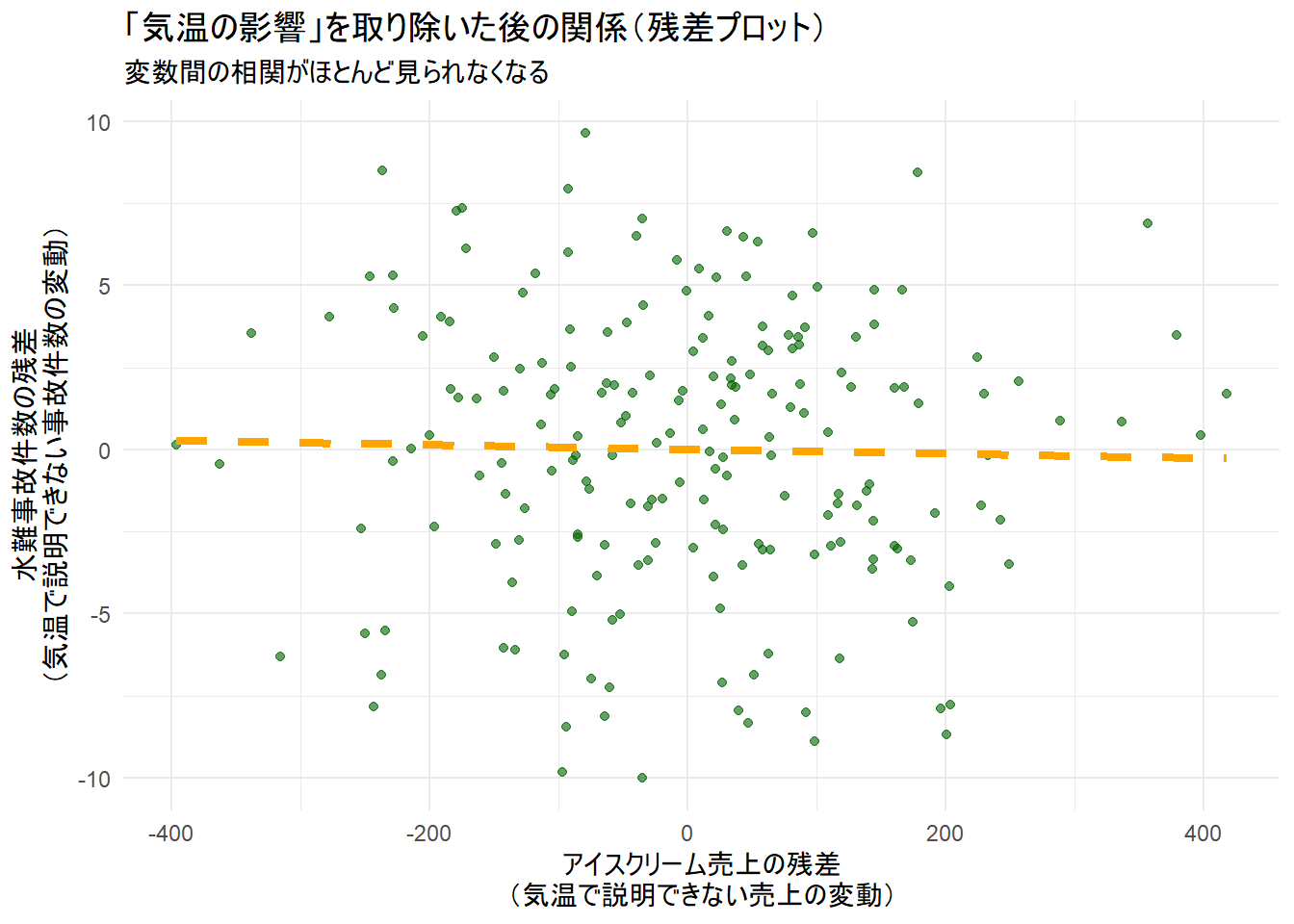
g2 <- ggplot(sim_data, aes(x = resid_ice, y = resid_jiko)) +
geom_point(alpha = 0.6, color = "darkgreen") +
geom_smooth(method = "lm", se = FALSE, color = "orange", linewidth = 1.5, linetype = "dashed") +
labs(
title = "「気温の影響」を取り除いた後の関係(残差プロット)",
subtitle = "変数間の相関がほとんど見られなくなる",
x = "アイスクリーム売上の残差\n(気温で説明できない売上の変動)",
y = "水難事故件数の残差\n(気温で説明できない事故件数の変動)"
) +
theme_minimal()
print(g2)--- 残差同士の相関分析 ---
残差同士の相関係数: -0.024この値は、先ほど計算した偏相関係数と一致します。
シミュレーション結果の解説
単純な相関分析: 最初の分析では、「アイスクリームの売上」と「水難事故の件数」の間に
0.633という強い正の相関が確認されました。散布図(Figure 1)を見ても、データは綺麗な右上がりの傾向を示しており、一見すると強い関係があるように見えます。偏相関分析: 次に、「気温」の影響を統制して偏相関係数を計算したところ、値は
-0.024とほぼ0になりました。これは、気温という共通の要因を取り除くと、アイスクリームの売上と水難事故の間にはもはや何の関係もないことを示唆しています。偏相関の概念の可視化: 最後の残差プロット(Figure 2)は、偏相関係数の意味を視覚的に示しています。
- 横軸は「気温では説明しきれなかったアイスクリーム売上の変動」
- 縦軸は「気温では説明しきれなかった水難事故件数の変動」
- Figure 2 では、点がランダムに散らばっており、明確な傾向(相関)は見られません。2つの変数の残差同士の相関係数も
-0.024となり、偏相関係数の値と一致していることが確認できます。
このシミュレーションを通じて、2つの変数間に強い相関が見られたとしても、それが必ずしも直接的な因果関係を意味するわけではなく、第3の変数による「見せかけの相関」である可能性を考慮することの重要性、そしてその検証に偏相関係数が有用であることが理解できます。
以上です。