Rで確率分布:ガンマ分布

Rで 確率分布:ガンマ分布 を試みます。

本ポストはこちらの続きです。

const typesetMath = (el) => { if (window.MathJax) { // MathJax Typeset window.MathJax.typeset(); } else if (window.katex...

1. ガンマ分布とは

ガンマ分布（Gamma Distribution）は、正の値をとる連続確率変数をモデル化するための、柔軟性の高い確率分布です。この分布は、指数分布やカイ2乗分布を一般化したものと見なすことができます。

ガンマ分布を理解する上で最も直感的なのは、「あるイベントがk回発生するまでの待ち時間」の分布という解釈です。指数分布が「イベントが1回起こるまでの待ち時間」をモデル化するのに対し、ガンマ分布はこれを一般化します。

確率密度関数 (Probability Density Function, PDF)

ガンマ分布に従う確率変数 \(X\) の確率密度関数 \(f(x)\) は、2つのパラメータを用いて以下のように定義されます。（Rの実装に合わせて、形状パラメータとレートパラメータで記述します）

\[f(x | \alpha, \beta) = \dfrac{\beta^\alpha}{\Gamma(\alpha)} x^{\alpha-1} e^{-\beta x} \quad (x \ge 0)\]

この関数は、2つのパラメータによってその形状が決定されます。

\(\alpha\) (アルファ): 形状パラメータ (shape parameter)
- 分布の形状を決定するパラメータです。「待ち時間」の文脈では、待つべきイベントの発生回数に相当します。
- \(\alpha\) が大きくなるにつれて、分布の歪みは小さくなり、左右対称な山型に近づいていきます。
\(\beta\) (ベータ): レートパラメータ (rate parameter)
- イベントが発生する平均的な頻度（レート）を表します。尺度パラメータ \(\theta\) とは \(\beta = 1/\theta\) の逆数の関係にあります。
- この値が大きくなると、イベントが頻繁に起こるため待ち時間は短くなり、分布は左に圧縮されます。
- この値が小さくなると、イベントが稀にしか起こらないため待ち時間は長くなり、分布は右に引き伸ばされます。

また、式中の \(\Gamma(\alpha)\) はガンマ関数と呼ばれ、階乗を実数や複素数に拡張したものです。\(\Gamma(\alpha) = \displaystyle\int_0^\infty t^{\alpha-1}e^{-t}dt\) で定義されます。

主な特徴

定義域: 確率変数は常に非負の値 (\(x \ge 0\)) をとります。
形状の多様性: 形状パラメータ \(\alpha\) の値によって、指数分布のような単調減少する形から、正規分布に似た対称な山型まで、様々な形状をとることができます。
代表値:
- 平均 (Mean): \(E[X] = \dfrac{\alpha}{\beta}\)
- 分散 (Variance): \(V[X] = \dfrac{\alpha}{\beta^2}\)
他の分布との関係（一般化としての役割）:
- 指数分布: 形状パラメータ \(\alpha=1\) のガンマ分布は、レートパラメータが \(\beta\) の指数分布と一致します。
- カイ2乗分布: 自由度 \(k\) のカイ2乗分布は、形状パラメータ \(\alpha=k/2\)、レートパラメータ \(\beta=1/2\) のガンマ分布と一致します。
- アーラン分布: 形状パラメータ \(\alpha\) が整数に限定されたガンマ分布は、アーラン分布と呼ばれます。

2. ガンマ分布の応用例

その柔軟性から、様々な分野で応用されています。

待ち行列理論・信頼性工学
- 顧客が \(k\) 人到着するまでの合計時間や、ある機械システムで \(k\) 個の部品が故障するまでの合計時間など、複数のイベントの累積待ち時間のモデル化に用いられます。
保険数理
- 保険会社が受け取る保険金請求の合計額をモデル化するのに使われます。個々の請求額が特定の分布に従うとき、その合計額の分布としてガンマ分布がしばしば現れます。
気象学
- 月間や年間の総降水量など、常に正の値を取り、右に裾を引くようなデータの分布をモデル化するのに適しています。
ベイズ統計学
- ポアソン分布や指数分布のレートパラメータ、または正規分布の精度（分散の逆数）に対する共役事前分布として用いられます。

3. R言語によるシミュレーション

ここでは、形状パラメータ \(\alpha\) とレートパラメータ \(\beta\) を変更した4つのガンマ分布を1枚のチャートに描画します。これにより、2つのパラメータが分布の形状に与える影響を視覚的に理解します。

ケース1: α=1, β=1 （指数分布と同一）
ケース2: α=2, β=1 （形状パラメータを大きくする → 山型に）
ケース3: α=5, β=1 （形状パラメータをさらに大きくする → より対称な山型に）
ケース4: α=5, β=0.5 （レートパラメータを小さくする → 分布が右に広がる）

# 必要なライブラリを読み込みます
library(ggplot2)
library(dplyr)
library(tidyr)

# 1. 描画範囲となるx軸の値を生成
x_vals <- seq(0, 20, length.out = 1000)

# 2. 異なるパラメータを持つガンマ分布の確率密度を計算
# dgamma(x, shape, rate) を使用。shapeがα, rateがβ
df <- tibble(
  x = x_vals
) %>%
  mutate(
    `α=1, β=1`   = dgamma(x, shape = 1, rate = 1),
    `α=2, β=1`   = dgamma(x, shape = 2, rate = 1),
    `α=5, β=1`   = dgamma(x, shape = 5, rate = 1),
    `α=5, β=0.5` = dgamma(x, shape = 5, rate = 0.5)
  )

# 3. ggplotで描画しやすいように、データを「ロングフォーマット」に変換
df_long <- df %>%
  pivot_longer(
    cols = -x,
    names_to = "parameters",
    values_to = "density"
  ) %>%
  # 凡例の順序を調整
  mutate(parameters = factor(parameters, levels = c(
    "α=1, β=1",
    "α=2, β=1",
    "α=5, β=1",
    "α=5, β=0.5"
  )))

# 4. 各分布に割り当てる色を定義
manual_colors <- c(
  `α=1, β=1`   = "blue",
  `α=2, β=1`   = "red",
  `α=5, β=1`   = "darkgreen",
  `α=5, β=0.5` = "purple"
)

# 5. ggplotを使用してチャートを描画
p <- ggplot(df_long, aes(x = x, y = density, color = parameters)) +
  geom_line(linewidth = 1.2) +
  scale_color_manual(values = manual_colors) +
  labs(
    title = "パラメータ(α, β)によるガンマ分布の変化",
    subtitle = "形状(α)は山の形、レート(β)は横のスケールを決定する",
    x = "待ち時間 (x)",
    y = "確率密度",
    color = "パラメータ (α, β)"
  ) +
  theme_minimal(base_size = 14) +
  theme(
    legend.position = "top",
    plot.title = element_text(face = "bold"),
    plot.subtitle = element_text(color = "gray40")
  )

# チャートの表示
print(p)

Figure 1 の解説

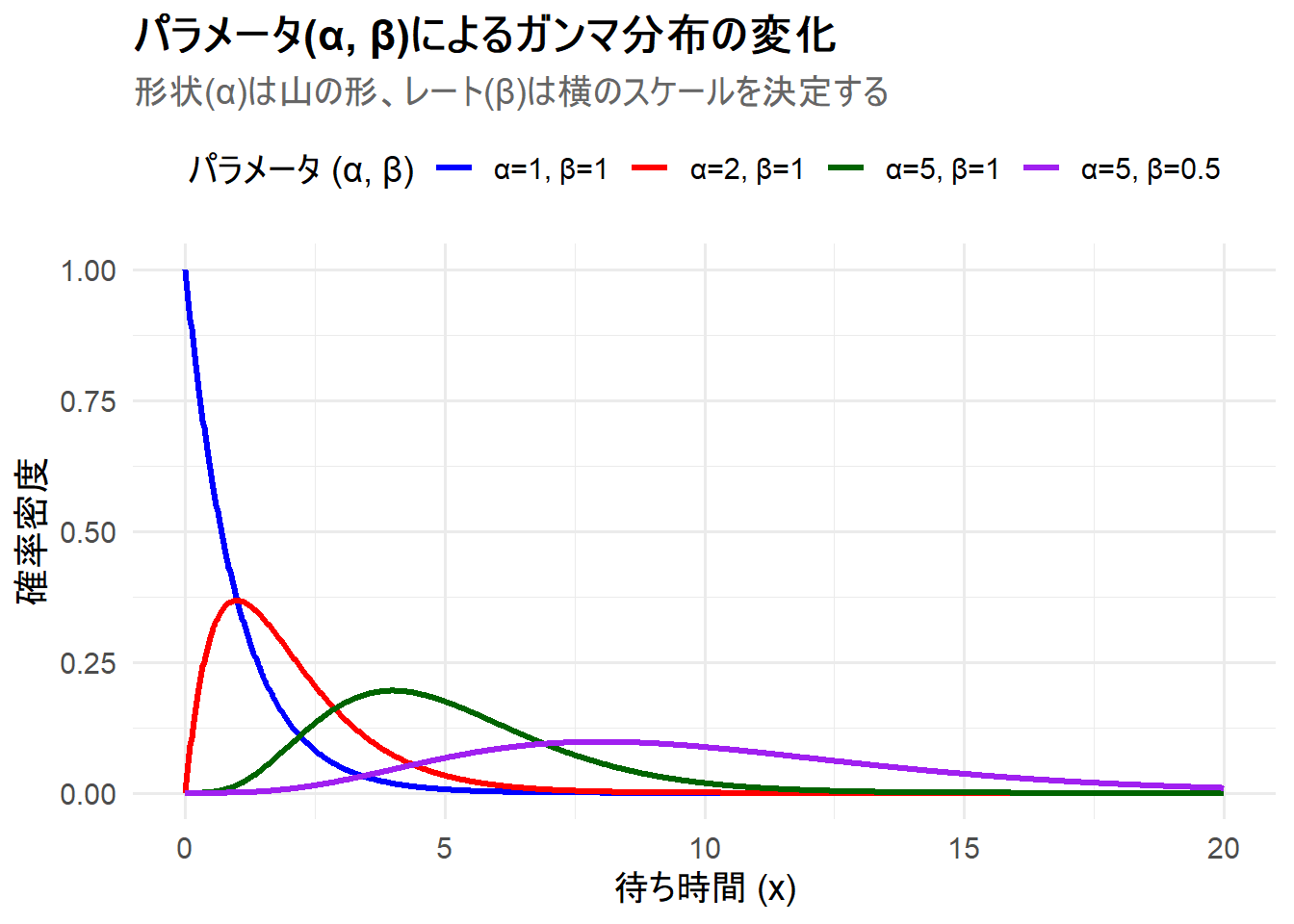
上記のRコードを実行すると、4つのガンマ分布が描画されたチャート Figure 1 が生成されます。

α=1, β=1 (青線): 形状パラメータが1ですので、これはレートが1の指数分布と一致します。
α=2, β=1 (赤線): 形状パラメータが2になり、分布は右に歪んだ山型になりました。これは「イベントが2回起こるまでの待ち時間」の分布に相当します。
α=5, β=1 (緑線): 形状パラメータが5に増えたことで、分布の山はさらに右にシフトし（平均が\(\alpha/\beta=5\)に）、形状もより左右対称に近づいています。
α=5, β=0.5 (紫線): 緑線と同じ形状パラメータですが、レートパラメータが半分になっています。これにより、平均は\(\alpha/\beta=10\)、分散は\(\alpha/\beta^2=20\)となり、緑線と比べて分布が大きく右にシフトし、より平たく広がっていることがわかります。これは、イベントの発生頻度が低いと、待ち時間が長くなり、ばらつきも大きくなるという直感に対応します。

以上です。