Rで 確率分布:グンベル分布 を試みます。
本ポストはこちらの続きです。

1. グンベル分布とは
グンベル分布(Gumbel Distribution)は、極値統計学(Extreme Value Theory, EVT)における3種類の極値分布(タイプI, II, III)のうち、タイプIに分類される連続確率分布です。
この分布は、正規分布や指数分布のような「軽い裾」を持つ分布から独立に抽出された多数の標本について、その標本ごとの最大値(または最小値)が従う分布をモデル化します。
確率密度関数 (Probability Density Function, PDF)
グンベル分布に従う確率変数 \(X\) の確率密度関数 \(f(x)\) は、2つのパラメータを用いて以下のように定義されます。
\[f\left(x | \mu, \sigma\right) = \dfrac{1}{\sigma} \exp\left(-\left(\dfrac{x-\mu}{\sigma} + e^{-(x-\mu)/\sigma}\right)\right)\]
この分布は、2つのパラメータによってその形状が決定されます。
- \(\mu\): 位置パラメータ (location parameter)
- 分布の最頻値(Mode)の位置を決定します。分布のピークがこの値になります。
- \(\sigma\): 尺度パラメータ (scale parameter)
- 分布の広がり(ばらつき)を決定する正のパラメータです。この値が大きいほど、分布は広く平たくなります。
主な特徴
- 定義域: 確率変数は実数全体(\(-\infty < x < \infty\))をとります。
- 形状: 非対称な形状をしており、最頻値よりも右側に長く裾を引く(右に歪んだ)分布です。これは、極端な最大値は青天井に大きくなりうるが、最小値側にはある程度の限界があるという直感に対応します。
- 代表値:
- 平均 (Mean): \(E[X] = \mu + \sigma \gamma\) (\(\gamma \approx 0.5772\) はオイラー・マスケローニ定数)
- 分散 (Variance): \(V[X] = \dfrac{\pi^2 \sigma^2}{6}\)
- 最頻値 (Mode): \(\mu\)
- 中央値 (Median): \(\mu - \sigma \ln(\ln 2)\)
- 理論的背景(フィッシャー・ティペット・グネデンコの定理): 正規分布、指数分布、ガンマ分布、ワイブル分布など、多くの一般的な分布からサンプリングされた最大値の分布は、サンプルサイズを大きくするとグンベル分布に収束することが知られています。
2. グンベル分布の応用例
「最大値」が問題となる様々な分野で応用されます。
- 水文学・気象学
- 年間最大降水量、年間最大風速、河川の年間最大流量、高潮の最大水位など、自然災害のリスク評価に不可欠です。これにより、堤防の設計に必要な「100年確率降水量」などを推定します。
- 構造工学
- 高層ビルや橋が、その耐用年数中に経験するであろう最大風圧や最大地震動を予測し、安全設計に役立てます。
- 金融・保険
- ある期間における資産の最大損失額や、保険金の最大請求額をモデル化し、リスク管理に利用されます。
- 材料科学
- 材料の最も弱い部分の強度(破壊強度)の分布をモデル化する際に、最小値の極値分布として利用されることがあります(最小値の分布は、最大値の分布の符号を反転させたものと等価です)。
3. R言語によるシミュレーション
ここでは、位置パラメータ \(\mu\) と尺度パラメータ \(\sigma\) を変更した3つのグンベル分布を1枚のチャートに描画します。これにより、各パラメータが分布の形状に与える影響を視覚的に理解します。
- ケース1:
μ=0, σ=1(標準グンベル分布) - ケース2:
μ=2, σ=1(位置パラメータをシフト → ピークが移動) - ケース3:
μ=0, σ=2(尺度パラメータを大きくする → 分布が広がる)
Rコード
# 必要なライブラリを読み込みます
library(evd)
library(ggplot2)
library(dplyr)
library(tidyr)
# 1. 描画範囲となるx軸の値を生成
x_vals <- seq(-5, 15, length.out = 1000)
# 2. 異なるパラメータを持つグンベル分布の確率密度を計算
# dgumbel(x, loc, scale) を使用
df <- tibble(
x = x_vals
) %>%
mutate(
`μ=0, σ=1` = dgumbel(x, loc = 0, scale = 1),
`μ=2, σ=1` = dgumbel(x, loc = 2, scale = 1),
`μ=0, σ=2` = dgumbel(x, loc = 0, scale = 2)
)
# 3. ggplotで描画しやすいように、データを「ロングフォーマット」に変換
df_long <- df %>%
pivot_longer(
cols = -x,
names_to = "parameters",
values_to = "density"
) %>%
# 凡例の順序を調整
mutate(parameters = factor(parameters, levels = c(
"μ=0, σ=1",
"μ=2, σ=1",
"μ=0, σ=2"
)))
# 4. 各分布に割り当てる色を定義
manual_colors <- c(
`μ=0, σ=1` = "blue",
`μ=2, σ=1` = "red",
`μ=0, σ=2` = "darkgreen"
)
# 5. ggplotを使用してチャートを描画
p <- ggplot(df_long, aes(x = x, y = density, color = parameters)) +
geom_line(linewidth = 1.2) +
scale_color_manual(values = manual_colors) +
labs(
title = "パラメータ(μ, σ)によるグンベル分布の変化",
subtitle = "最大値の分布をモデル化するのに適した、右に歪んだ形状を持つ",
x = "xの値",
y = "確率密度",
color = "パラメータ (μ, σ)"
) +
theme_minimal(base_size = 14) +
theme(
legend.position = "top",
plot.title = element_text(face = "bold"),
plot.subtitle = element_text(color = "gray40")
)
# チャートの表示
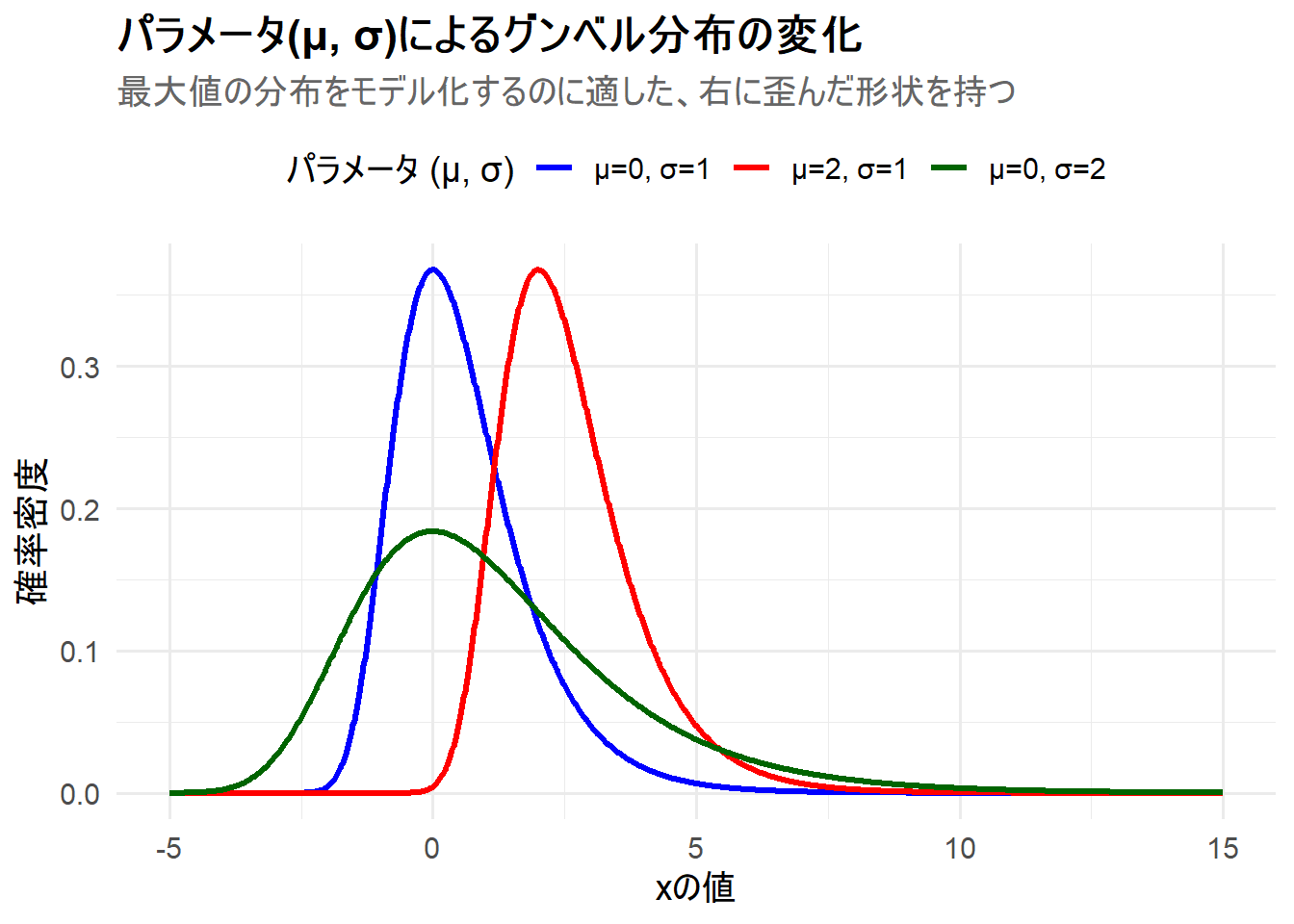
print(p)Figure 1 の解説
上記のRコードを実行すると、3つのグンベル分布が描画されたチャート Figure 1 が生成されます。
-
μ=0, σ=1(青線): 基準となる標準グンベル分布です。ピーク(最頻値)が\(x=0\)にあり、右側に長く裾を引く非対称な形状をしていることがわかります。 -
μ=2, σ=1(赤線): 位置パラメータ \(\mu\) を2にしたことで、分布の形状はそのままに、ピークが\(x=2\)の位置に平行移動しています。 -
μ=0, σ=2(緑線): 尺度パラメータ \(\sigma\) を2倍にしたことで、分布のピークは\(x=0\)のままですが、山は低くなり、全体としてより広く平たい分布になっています。これは、最大値のばらつきがより大きい状況を表しています。
4. フィッシャー・ティペット・グネデンコの定理のシミュレーション
この定理は「十分に多くの独立同分布に従う確率変数があるとき、その中の最大値(または最小値)が従う分布は、サンプルサイズを大きくしていくと、グンベル分布、フレシェ分布、ワイブル分布(の逆)のいずれかの極値分布族に収束する」というものです。
元の分布が正規分布や指数分布のような「軽い裾」を持つ場合、最大値の分布はグンベル分布に収束します。ここでは、この定理が実際に成り立つ様子を、シミュレーションを通じて可視化します。
シミュレーションのステップ
- 元の分布を決める: ここでは、標準正規分布 \(N(0, 1)\) を選びます。
- サンプリング:
- 正規分布から、\(n\) 個の乱数を1セットとしてサンプリングします。
- そのセットの中から最大値を一つだけ取り出します。
- このプロセスを、多数回(10,000回)繰り返します。
- 分布の確認:
- 集めた10,000個の「最大値たち」の分布をヒストグラムで可視化します。
- そのヒストグラムに、理論的に予測されるグンベル分布の確率密度関数を重ねて描き、両者がどれだけ一致するかを確認します。
- サンプルサイズ \(n\) の影響:
- ステップ2のサンプルサイズ \(n\) を、小さい値(\(n=10\))から大きい値(\(n=100, n=10000\))へと変えていき、分布の形状がどのようにグンベル分布に収束していくかを観察します。
Rコード
# シミュレーションの設定
seed <- 20250808
set.seed(seed)
num_simulations <- 10000
sample_sizes <- c(10, 100, 10000)
# シミュレーションの実行
simulation_results <- lapply(sample_sizes, function(n) {
max_values <- replicate(num_simulations, max(rnorm(n)))
tibble(
n = paste0("n = ", n),
max_value = max_values
)
}) %>%
bind_rows()
# 理論的なグンベル分布のパラメータを計算
gumbel_params <- tibble(
n_val = sample_sizes
) %>%
mutate(
c_n = sqrt(2 * log(n_val)),
d_n = c_n - (log(log(n_val)) + log(4 * pi)) / (2 * c_n),
loc = d_n,
scale = 1 / c_n,
n = paste0("n = ", n_val)
)
# 可視化
p_simulation <- ggplot(simulation_results, aes(x = max_value)) +
# ヒストグラムを描画
geom_histogram(aes(y = after_stat(density)), bins = 50, fill = "lightblue", color = "black") +
# 理論的なグンベル分布の曲線を描画
# 別のデータフレーム(gumbel_params)を使うため、geom_line() を使用
geom_line(
data = . %>% distinct(n) %>% left_join(gumbel_params, by = "n") %>%
rowwise() %>%
mutate(x_range = list(seq(min(simulation_results$max_value[simulation_results$n == n]),
max(simulation_results$max_value[simulation_results$n == n]),
length.out = 200
))) %>%
unnest(x_range) %>%
mutate(density = dgumbel(x_range, loc = loc, scale = scale)),
aes(x = x_range, y = density, color = "理論値 (グンベル分布)"),
linewidth = 1.2,
# ggplot() の aes(x = max_value) を継承しない
inherit.aes = FALSE
) +
# ファセットで分割
facet_wrap(~n, scales = "free") +
scale_color_manual(values = c("理論値 (グンベル分布)" = "red")) +
labs(
title = "フィッシャー・ティペット・グネデンコの定理のシミュレーション",
subtitle = "正規分布からの最大値の分布は、サンプルサイズ(n)が大きいほどグンベル分布に近づく",
x = "各サンプルセットの最大値",
y = "確率密度",
color = ""
) +
theme_minimal(base_size = 14) +
theme(
legend.position = "top",
plot.title = element_text(face = "bold"),
plot.subtitle = element_text(color = "gray40", size = 12),
strip.text = element_text(face = "bold", size = 12)
)
# チャートの表示
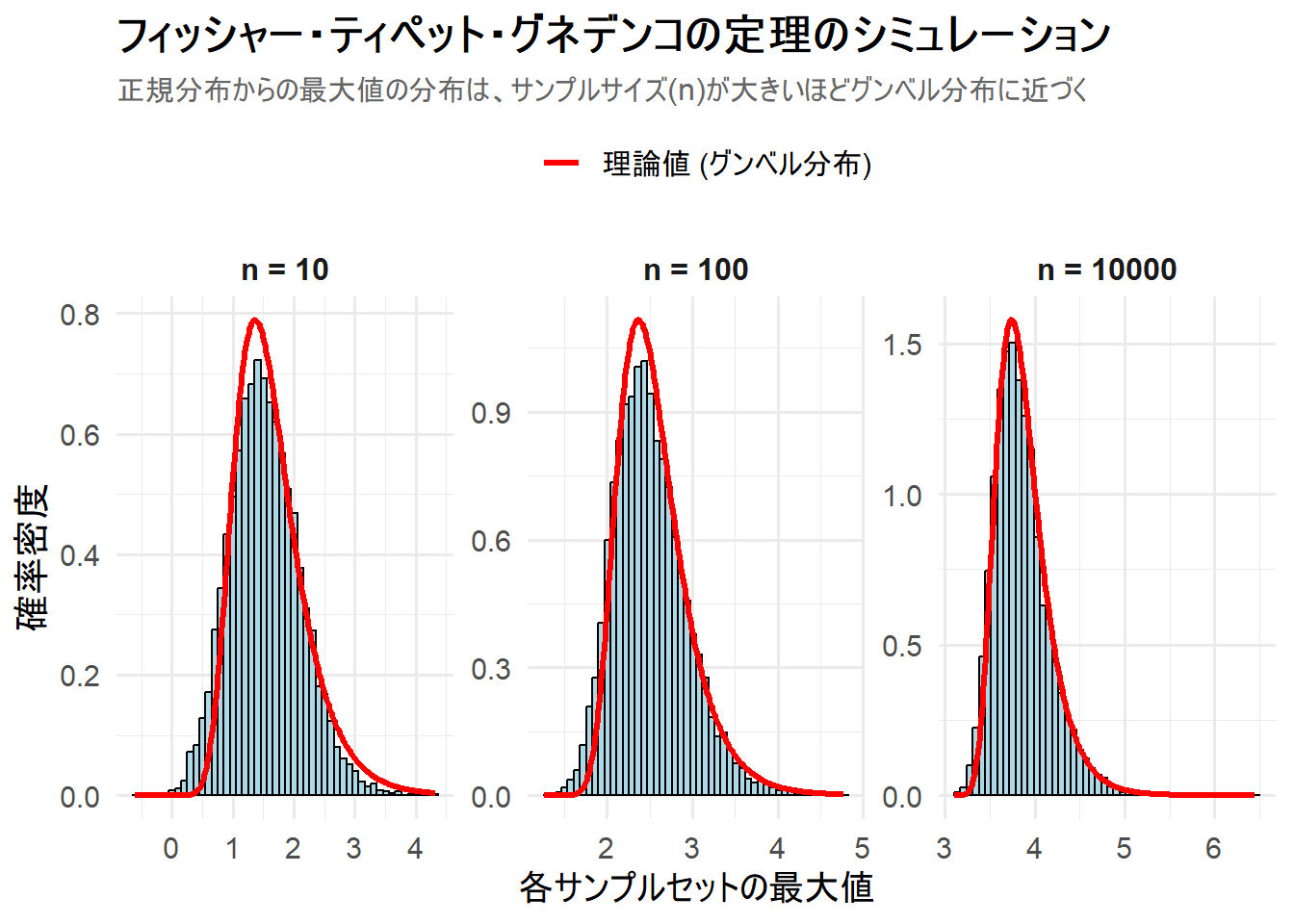
print(p_simulation)Figure 2 の解説
上記のRコードを実行すると、3つのサンプルサイズにおける最大値の分布を可視化したチャート Figure 2 が生成されます。
-
n = 10(左パネル):- 正規分布から10個だけサンプリングした場合、その最大値の分布(ヒストグラム)は、まだ少し左右対称に近い形をしています。
- しかし、既に右に裾を引く非対称な形状の兆候が見られ、理論的なグンベル分布の曲線(赤線)に大まかには沿っていますが、まだ完全には一致していません。
-
n = 100(中パネル):- サンプルサイズが100に増えると、最大値の分布はより顕著に右に歪んだ形状になります。
- ヒストグラムの形状は、理論的なグンベル分布の曲線(赤線)に非常によくフィットするようになっています。
-
n = 10000(右パネル):- サンプルサイズが10000になると、最大値の分布(ヒストグラム)と理論的なグンベル分布の曲線(赤線)は、ほぼ一致します。
- また、最大値の分布全体が、n=100の時よりもさらに右にシフトしていることもわかります。これは、より多くのサンプルの中から最大値を選ぶため、より大きな値が出やすくなるという直感と一致します。
以上です。