Rで コンドルセの陪審定理 を試みます。
1. コンドルセの陪審定理とは
コンドルセの陪審定理(Condorcet’s Jury Theorem)とは、集団による意思決定の正しさに関する確率的な定理です。18世紀のフランスの思想家、数学者であるコンドルセ侯爵によって提唱されました(陪審定理)。
この定理の要点は以下の通りです。
ある集団(陪審員、専門家、投票者など)が、2つの選択肢(例:有罪か無罪、正しいか間違いか)の中から多数決で1つを選ぶ状況を考えます。
- 個々のメンバーの判断が「正しい」確率 (
p) が50%をわずかでも超えている場合(p > 0.5):- 集団の人数を増やせば増やすほど、集団全体が多数決によって「正しい」判断を下す確率は100%(確率1)に近づきます。
- 個々のメンバーの判断が「正しい」確率 (
p) が50%未満の場合(p < 0.5):- 集団の人数を増やせば増やすほど、集団全体が多数決によって「正しい」判断を下す確率は0%(確率0)に近づきます。
- つまり、間違った判断をする傾向のある人々をいくら集めても、より悪い結果を招くだけということになります。これは「衆愚」に陥る危険性を示唆します。
- 個々のメンバーの判断が「正しい」確率 (
p) がちょうど50%の場合(p = 0.5):- 集団の人数を増やしても、集団全体が正しい判断をする確率は50%のまま変わりません。これは、コイン投げで決めるのと変わらない状態です。
この定理は、「三人寄れば文殊の知恵」のような「集団の意思決定は常に優れている」と無条件に主張するものではなく、「個々のメンバーの質(正解率が50%を超えているか)が決定的に重要である」という重要な示唆を与えてくれます。
2. シミュレーションのシナリオ
シナリオ:新製品「コンドルセ」発売の是非
ある飲料メーカーが、これまでにない革新的な健康飲料「コンドルセ」を開発しました。このドリンクは、市場に受け入れられれば大ヒット商品になる可能性を秘めていますが、消費者の好みに合わなければ全く売れずに大失敗に終わるリスクも抱えています。
経営陣は、この「コンドルセ」を発売すべきかどうかの最終判断を下すために、社内の様々な部署から専門家を集めて評価チームを結成し、多数決で意思決定を行うことにしました。
ここで、「コンドルセ」は本当に消費者に支持され、発売すれば「ヒットする」のが隠された真実だとします。つまり、チームが「発売すべき」と判断することが「正しい決定」です。
このシミュレーションでは、専門家チームの特性によって2つのケースを考えます。
- ケースA:先進的な専門家チーム(個々の正解率 p = 0.6)
- メンバーは市場のトレンドに明るく、新しいコンセプトを受け入れる能力が高い。
- 各メンバーが「この商品はヒットする」と正しく見抜く確率は60%です。
- ケースB:保守的な専門家チーム(個々の正解率 p = 0.4)
- メンバーは過去の成功体験に囚われ、革新的な製品に対して懐疑的。
- 各メンバーが「この商品はヒットする」と正しく見抜く確率は40%しかありません(つまり、60%の確率で「失敗するだろう」と誤った判断をします)。
シミュレーションの問い: この2つのチームで、人数を増やしていくと、チーム全体として「発売すべき」という正しい決定を下す確率はどのように変化するでしょうか?
3. R言語によるシミュレーションコードと結果
以下に、上記のシナリオに基づいたシミュレーションを実行するRコードと、その結果のプロット、そして解説を示します。
Rコード
seed <- 20250801
set.seed(seed)
# 必要なライブラリを読み込む
library(ggplot2)
library(dplyr)
library(scales) # y軸をパーセント表示にするために使用
# ---- パラメータ設定 ----
# 専門家チームの人数 (1人から101人までの奇数)
# 奇数にして、多数決における『同数(引き分け)』の発生を避け、シミュレーションを単純化する
n_values <- seq(1, 101, by = 2)
# 専門家個人の正解率 (p)
# ケースA: 先進的なチーム (p=0.6)
# ケースB: 保守的なチーム (p=0.4)
p_values <- c(0.6, 0.4)
# 各設定でのシミュレーション試行回数
n_sims <- 2000
# 結果を格納するデータフレームを作成
results <- expand.grid(n = n_values, p = p_values)
results$correct_decision_prob <- NA # 結果を格納する列を追加
# ---- シミュレーション実行 ----
for (i in 1:nrow(results)) {
n <- results$n[i]
p <- results$p[i]
# n_sims回、多数決シミュレーションを行う
# rbinomで、n人の専門家がpの確率で正しい判断(1)をする試行をn_sims回行う
sim_results <- rbinom(n_sims, n, p)
# 多数決で正しい判断となるのは、正しい判断をした人数が半数を超える場合
correct_decisions <- sum(sim_results > (n / 2))
# 集団が正しい判断をした確率を計算
results$correct_decision_prob[i] <- correct_decisions / n_sims
}
# ---- 結果の可視化 ----
# 凡例ラベル用のファクターを作成
results$team_type <- factor(
results$p,
levels = c(0.6, 0.4),
labels = c("先進的なチーム (p=0.6)", "保守的なチーム (p=0.4)")
)
# グラフの作成
g <- ggplot(results, aes(x = n, y = correct_decision_prob, color = team_type)) +
geom_line(linewidth = 1.2) +
geom_hline(yintercept = 0.5, linetype = "dashed", color = "black") +
scale_y_continuous(labels = scales::percent_format(accuracy = 1), limits = c(0, 1)) +
scale_color_manual(values = c("先進的なチーム (p=0.6)" = "#0072B2", "保守的なチーム (p=0.4)" = "#D55E00")) +
labs(
title = "コンドルセの陪審定理シミュレーション:専門家チームの人数と判断の正しさ",
subtitle = "新製品「コンドルセ」を発売すべきか?",
x = "専門家チームの人数",
y = "チームが「発売すべき」と正しく判断する確率",
color = "専門家チームのタイプ"
) +
theme_minimal() +
theme(
legend.position = "bottom",
plot.title = element_text(face = "bold", size = 14),
plot.subtitle = element_text(size = 14)
)
# グラフを表示
print(g)実行結果
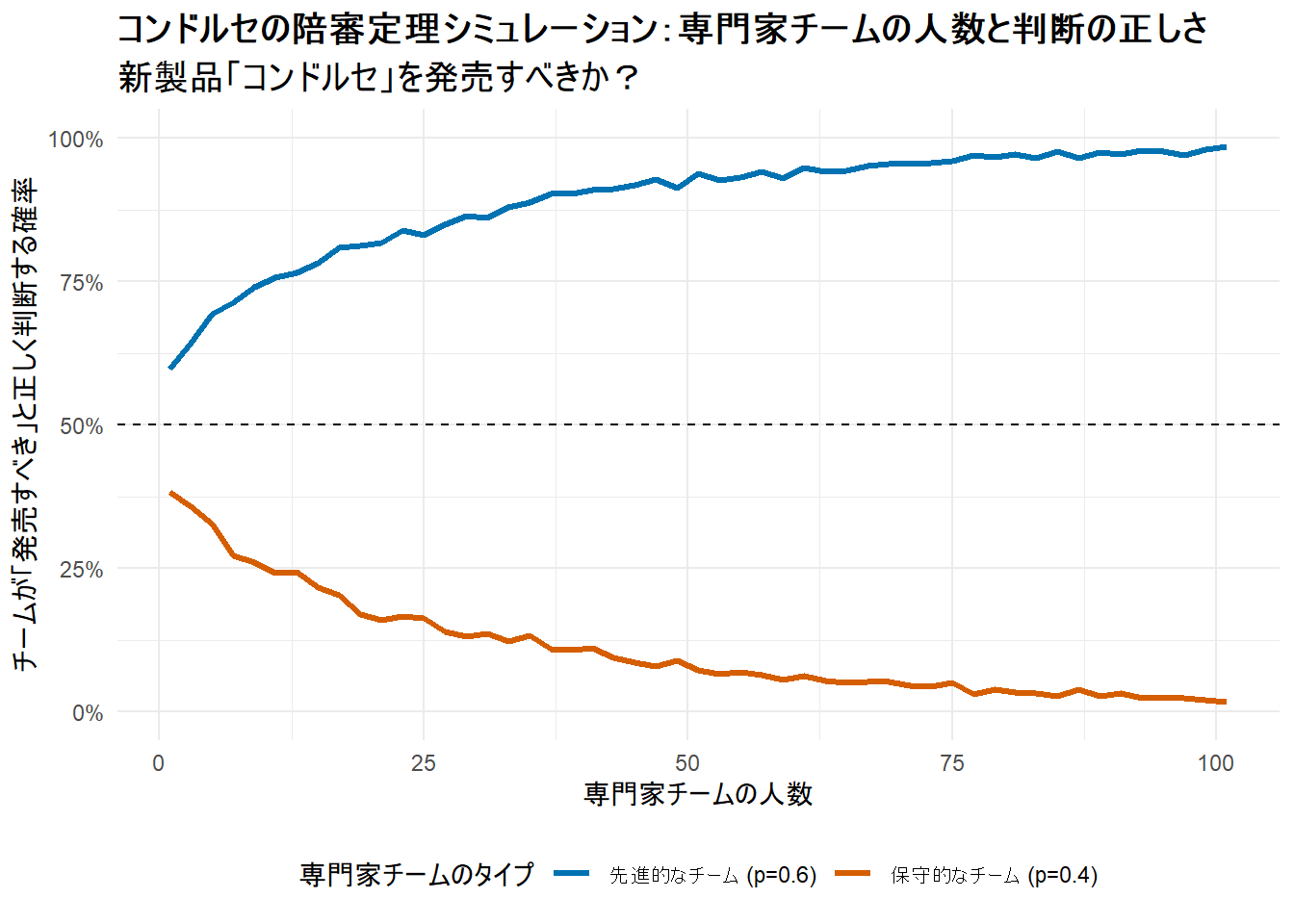
Figure 1 は、専門家チームの人数(横軸)が増えるにつれて、チーム全体が「コンドルセ」を発売すべきだと正しく判断する確率(縦軸)がどう変化するかを示しています。
先進的なチーム(青い線, p=0.6)
個々のメンバーが60%の確率で正しい判断をするこのチームでは、人数が増えるほど、集団としての判断が正しくなる確率が上昇し続け、100%に近づいています。
これは、個々のわずかな知恵が集まることで、賢明な「衆知」が生まれることを示しています。
保守的なチーム(オレンジの線, p=0.4)
個々のメンバーの正解率が40%しかないこのチームでは、全く逆の結果になっています。
人数を増やせば増やすほど、集団として正しい判断をする確率は下がり続け、0%に近づいていきます。
これは、誤った見識を持つメンバーを増やすと、集団はより確実に間違った結論(この場合はヒット商品を見逃す)に至る「衆愚」の状態を表しています。
結論
このシミュレーションは、コンドルセの陪審定理が示すように、多数決が常に良い結果を生むとは限らないことを示しています。
集団による意思決定の質は、メンバーを増やすこと以上に、その集団を構成する個々のメンバーの質(判断の正しさが50%を超えているか)に根本的に依存しているのです。
以上です。