Rで 確率分布:フォン・ミーゼス分布 を試みます。
本ポストはこちらの続きです。

1. フォン・ミーゼス分布とは
フォン・ミーゼス分布(von Mises Distribution)は、円周上のデータ(角度データ)のモデル化に利用させる連続確率分布です。
データの定義域が \([0, 2\pi)\) や \((-\pi, \pi]\) といった、周期的な性質を持つ角度や方向、時刻などを扱う際に有用です。
確率密度関数 (Probability Density Function, PDF)
フォン・ミーゼス分布に従う角度 \(\theta\) の確率密度関数 \(f(\theta)\) は、2つのパラメータを用いて以下のように定義されます。
\[f\left(\theta | \mu, \kappa\right) = \dfrac{e^{\kappa \cos(\theta - \mu)}}{2\pi I_0(\kappa)} \quad (0 \le \theta < 2\pi)\]
この分布は、2つのパラメータによってその形状が決定されます。
- \(\mu\): 平均方向 (mean direction)
- 分布の中心となる角度を決定します。確率密度が最も高くなる方向(最頻値)です。
- \(\kappa\): 集中度パラメータ (concentration parameter)
- 分布が平均方向 \(\mu\) の周りにどれだけ集中しているかを表す正のパラメータです。正規分布の精度(分散の逆数)に似た役割を果たします。
- \(\kappa = 0\): データはどの方向にも均等に分布します。これは円周上の一様分布と一致します。
- \(\kappa\) が大きい: データは平均方向 \(\mu\) の周りに強く集中し、分布はシャープで尖った形状になります。\(\kappa\) が大きいとき、この分布は平均 \(\mu\)、分散 \(1/\kappa\) の正規分布で近似できます。
- 分布が平均方向 \(\mu\) の周りにどれだけ集中しているかを表す正のパラメータです。正規分布の精度(分散の逆数)に似た役割を果たします。
また、式中の \(I_0(\kappa)\) は0次の第1種変形ベッセル関数と呼ばれ、確率密度関数の面積が1になるように調整する正規化定数です。
主な特徴
- 定義域: 円周上、すなわち \([0, 2\pi)\) のような周期的な区間です。
- 形状: 平均方向 \(\mu\) を中心に左右対称な釣鐘型をしています。
- 周期性: \(f(\theta) = f(\theta + 2\pi)\) という周期性を持ちます。
- 他の分布との関係:
- 集中度 \(\kappa=0\) のとき、円周上の一様分布になります。
- 集中度 \(\kappa\) が大きいとき、正規分布で近似されます。
2. フォン・ミーゼス分布の応用例
角度や方向、周期的な時間など、円周上のデータを扱う様々な分野で応用されます。
- 生物学
- 渡り鳥が飛ぶ方角、ウミガメが産卵のために帰る海岸の方向、動物の帰巣本能における移動方向など、動物行動学で利用されます。
- 地球科学・気象学
- 風向、海流の方向、地層の断層面の向きといった方向データの統計的モデリングに用いられます。
- 医学・神経科学
- 概日リズム(サーカディアンリズム)における活動のピーク時刻や、ニューロンの発火位相など、周期的な生命現象の分析に活用されます。
- 画像処理・バイオインフォマティクス
- タンパク質の二面角の分布や、画像中のテクスチャの方向性の分析などに使われます。
3. R言語によるシミュレーション
ここでは、集中度パラメータ \(\kappa\) と平均方向 \(\mu\) を変更した4つのフォン・ミーゼス分布を1枚のチャートに描画します。これにより、パラメータが分布の形状に与える影響を視覚的に理解します。
- ケース1:
μ=0, κ=0(円周上の一様分布) - ケース2:
μ=0, κ=1(少し集中した分布) - ケース3:
μ=0, κ=4(強く集中した分布) - ケース4:
μ=π, κ=4(平均方向をシフト)
Rコード
# 必要なライブラリを読み込みます
library(circular)
library(ggplot2)
library(dplyr)
library(tidyr)
# 1. 描画範囲となるx軸(角度)の値を生成 (0から2πラジアンまで)
x_vals <- seq(0, 2 * pi, length.out = 1000)
# 2. 異なるパラメータを持つフォン・ミーゼス分布の確率密度を計算
# dvonmises(x, mu, kappa) を使用
df <- tibble(
x = x_vals
) %>%
mutate(
`μ=0, κ=0` = dvonmises(x, mu = circular(0), kappa = 0),
`μ=0, κ=1` = dvonmises(x, mu = circular(0), kappa = 1),
`μ=0, κ=4` = dvonmises(x, mu = circular(0), kappa = 4),
`μ=π, κ=4` = dvonmises(x, mu = circular(pi), kappa = 4)
)
# 3. ggplotで描画しやすいように、データを「ロングフォーマット」に変換
df_long <- df %>%
pivot_longer(
cols = -x,
names_to = "parameters",
values_to = "density"
) %>%
# 凡例の順序を調整
mutate(parameters = factor(parameters, levels = c(
"μ=0, κ=0",
"μ=0, κ=1",
"μ=0, κ=4",
"μ=π, κ=4"
)))
# 4. 各分布に割り当てる色を定義
manual_colors <- c(
`μ=0, κ=0` = "black",
`μ=0, κ=1` = "blue",
`μ=0, κ=4` = "red",
`μ=π, κ=4` = "darkgreen"
)
# 5. ggplotを使用してチャートを描画
p <- ggplot(df_long, aes(x = x, y = density, color = parameters)) +
geom_line(linewidth = 1.2) +
scale_color_manual(values = manual_colors) +
# x軸のラベルをラジアン表記にする
scale_x_continuous(
breaks = c(0, pi / 2, pi, 3 * pi / 2, 2 * pi),
labels = c("0", "π/2", "π", "3π/2", "2π")
) +
labs(
title = "フォン・ミーゼス分布の変化",
subtitle = "集中度(κ)は分布の鋭さ、平均方向(μ)はピークの位置を決定する",
x = "角度 θ (ラジアン)",
y = "確率密度",
color = "パラメータ (μ, κ)"
) +
theme_minimal(base_size = 14) +
theme(
legend.position = "top",
plot.title = element_text(face = "bold"),
plot.subtitle = element_text(color = "gray40")
) +
guides(color = guide_legend(nrow = 2))
# チャートの表示
print(p)Figure 1 の解説
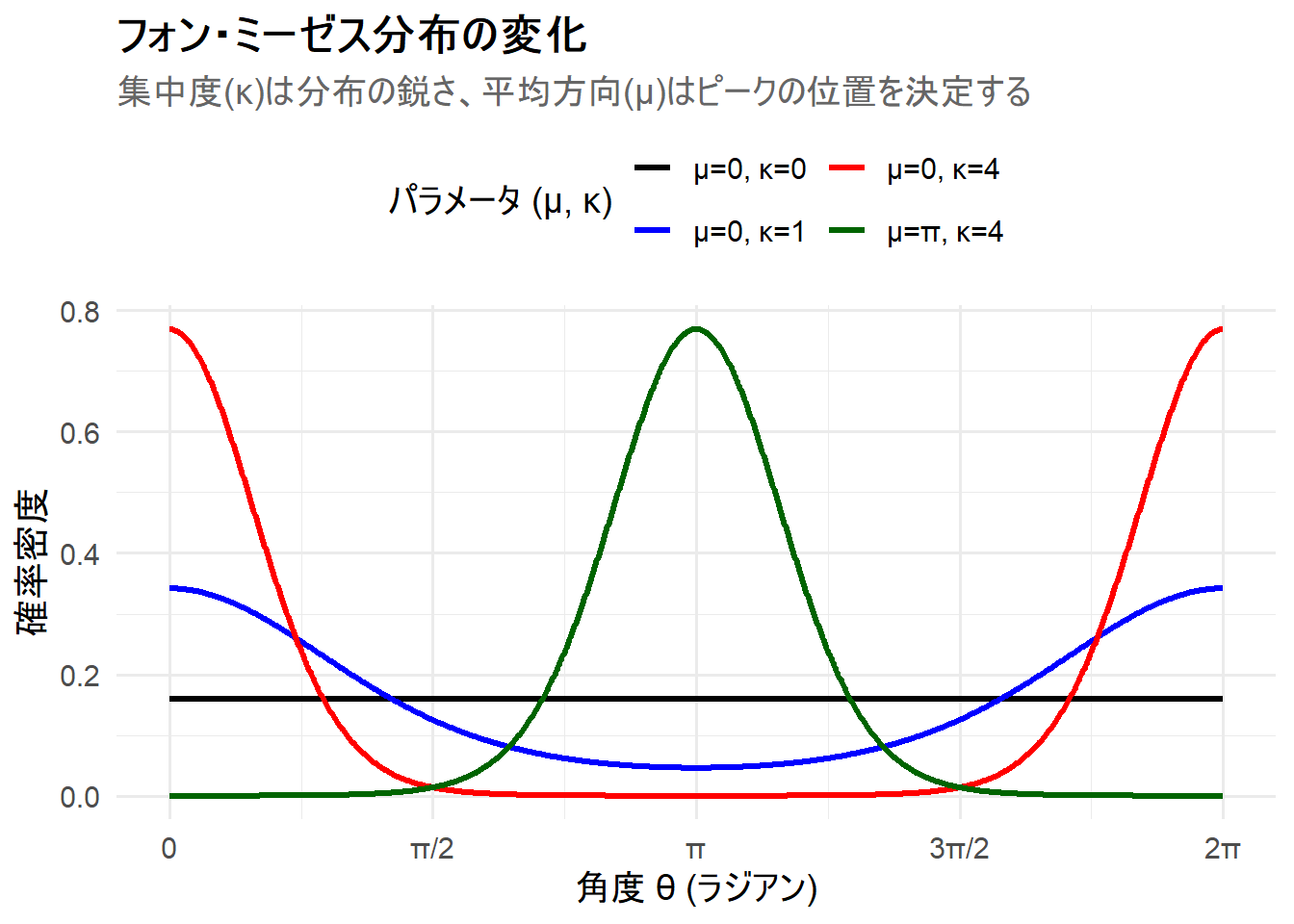
上記のRコードを実行すると、4つのフォン・ミーゼス分布が描画されたチャート Figure 1 が生成されます。
-
μ=0, κ=0(黒線): 集中度パラメータ \(\kappa\) が0なので、確率密度はどの角度でも一定の値をとります。これは円周上の一様分布であり、完全に平らな直線になっています。 -
μ=0, κ=1(青線): 集中度が1となり、平均方向である0ラジアンを中心に盛り上がった分布になっています。 -
μ=0, κ=4(赤線): 集中度が4に増えたことで、分布は0ラジアンを中心にさらに強く集中し、鋭く尖った山型の形状になっています。 -
μ=π, κ=4(緑線): 集中度は赤線と同じ4ですが、平均方向が \(\pi\)(180度)に設定されています。そのため、赤線と全く同じ形状の分布が、中心を \(\pi\) にして平行移動していることがわかります。
このシミュレーションから、フォン・ミーゼス分布がパラメータ \(\kappa\) によって「方向のばらつき具合」を、\(\mu\) によって「中心となる方向」を、それぞれ独立にコントロールできる、角度データを扱う上で有用な分布であることが理解できます。
以上です。