Rで 確率分布:フレシェ分布 を試みます。
本ポストはこちらの続きです。

1. フレシェ分布とは
フレシェ分布(Fréchet Distribution)は、極値統計学(EVT)における3種類の極値分布のうち、タイプIIに分類される連続確率分布です。
この分布は、パレート分布やコーシー分布のような裾が非常に重い(ヘビーテール)分布から独立に抽出された多数の標本について、その標本ごとの最大値が従う分布をモデル化します。グンベル分布が「軽い裾」の分布の最大値を扱うのに対し、フレシェ分布は「重い裾」の分布の最大値を扱う点が本質的な違いです。
確率密度関数 (Probability Density Function, PDF)
フレシェ分布に従う確率変数 \(X\) の確率密度関数 \(f(x)\) は、3つのパラメータを用いて以下のように定義されます。
\[f\left(x | \alpha, \sigma, \mu\right) = \dfrac{\alpha}{\sigma} \left(\dfrac{x-\mu}{\sigma}\right)^{-1-\alpha} \exp\left(-\left(\dfrac{x-\mu}{\sigma}\right)^{-\alpha}\right) \quad (x > \mu)\]
この分布は、3つのパラメータによってその形状が決定されます。
- \(\mu\): 位置パラメータ (location parameter)
- 分布の下限を決定します。確率変数 \(X\) は常に \(\mu\) より大きい値をとります。
- \(\sigma\): 尺度パラメータ (scale parameter)
- 分布の広がりを決定する正のパラメータです。
- \(\alpha\): 形状パラメータ (shape parameter)
- 分布の裾の重さを決定する正のパラメータです。この値が小さいほど、裾はより重くなります。
主な特徴
- 定義域: 確率変数は、位置パラメータ \(\mu\) より大きい値 (\(x > \mu\)) をとります。
- 形状: 右に非常に長く重い裾を持つ、非対称な(右に歪んだ)形状をしています。
- 平均・分散の存在条件: パレート分布と同様に、形状パラメータ \(\alpha\) の値によって平均や分散が存在しない場合があります。
- 平均 (Mean): \(\mu + \sigma \Gamma(1-1/\alpha)\) (ただし、\(\alpha > 1\) の場合のみ存在)
- 分散 (Variance): \(\sigma^2 (\Gamma(1-2/\alpha) - (\Gamma(1-1/\alpha))^2)\) (ただし、\(\alpha > 2\) の場合のみ存在)
- 理論的背景(フィッシャー・ティペット・グネデンコの定理): パレート分布、コーシー分布、t分布など、裾がべき乗的に減衰する分布からサンプリングされた最大値の分布は、サンプルサイズを大きくするとフレシェ分布に収束します。
2. フレシェ分布の応用例
グンベル分布と同様に「最大値」が問題となりますが、特に極端な値がより発生しやすいと考えられる現象に適用されます。
- 金融・保険
- 株式市場の最大損失、保険金の最大請求額など、潜在的に青天井であり、かつ壊滅的な規模になりうる極端なイベントのモデリング。グンベル分布よりもさらに保守的な(より大きなリスクを見積もる)リスク評価が可能になります。
- 水文学
- 特に「非常に稀だが極めて大規模な」洪水(例: 1000年確率洪水)の流量をモデル化する際に、グンベル分布よりも現実的な結果を与えることがあります。
- 材料科学
- 脆性材料の破壊強度など、材料中の最も重大な欠陥によって全体の強度が決まるような現象のモデリング。
- インターネットトラフィック
- ファイルサイズやダウンロード時間など、ごく一部の非常に大きなファイルが全体のトラフィックに大きな影響を与えるような状況の分析。
3. R言語によるシミュレーション
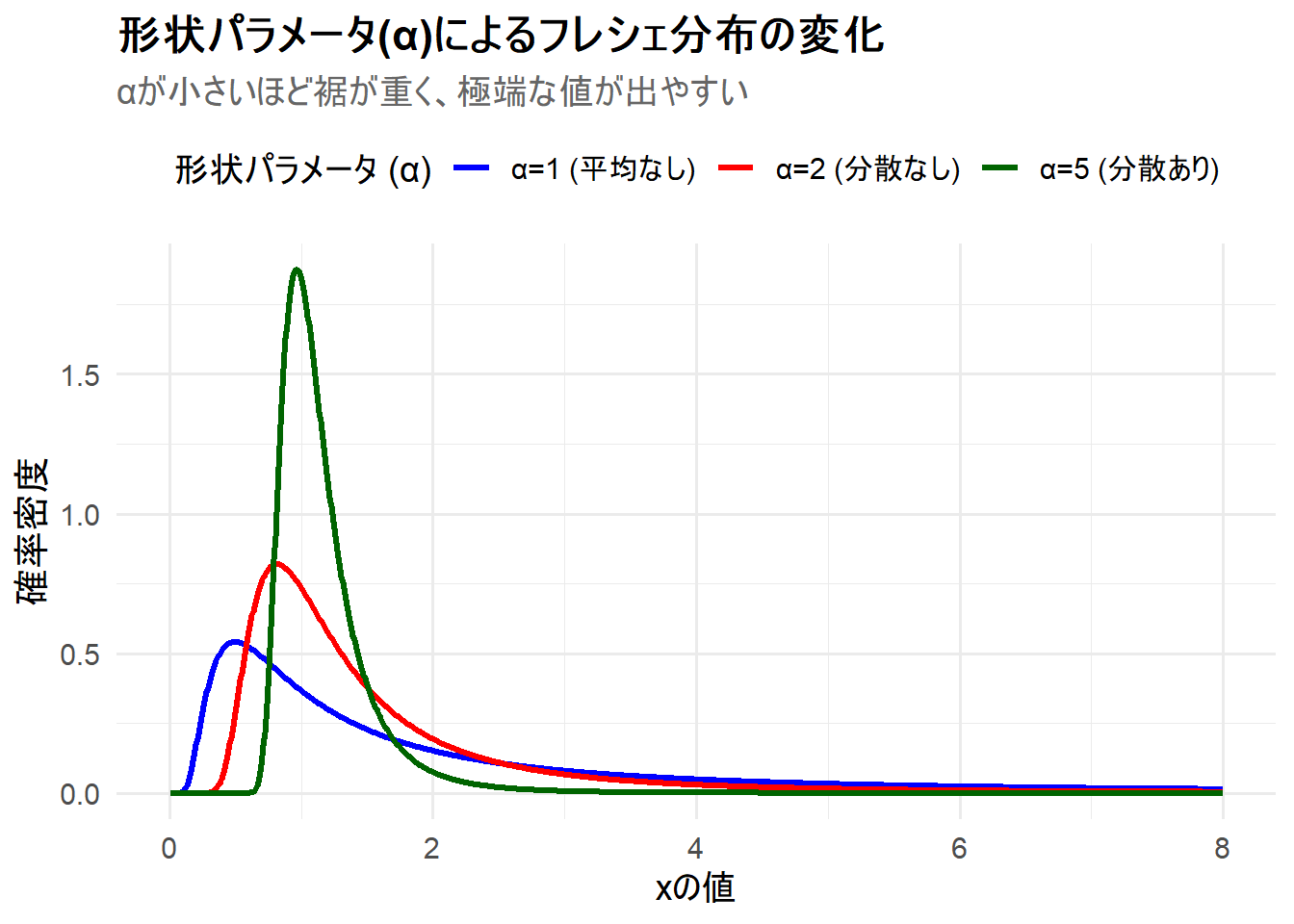
ここでは、形状パラメータ \(\alpha\) を変更した3つのフレシェ分布を1枚のチャートに描画します。
- ケース1:
α=1(裾が非常に重く、平均が存在しない) - ケース2:
α=2(平均は存在するが、分散が存在しない) - ケース3:
α=5(平均・分散ともに存在する、裾が比較的軽い)
Rコード
# 必要なライブラリを読み込みます
library(evd)
library(ggplot2)
library(dplyr)
library(tidyr)
# 1. 描画範囲となるx軸の値を生成
x_vals <- seq(0.01, 8, length.out = 1000)
# 2. 異なるパラメータを持つフレシェ分布の確率密度を計算
# dfrechet(x, loc, scale, shape) を使用
df <- tibble(
x = x_vals
) %>%
mutate(
`α=1 (平均なし)` = dfrechet(x, loc = 0, scale = 1, shape = 1),
`α=2 (分散なし)` = dfrechet(x, loc = 0, scale = 1, shape = 2),
`α=5 (分散あり)` = dfrechet(x, loc = 0, scale = 1, shape = 5)
)
# 3. ggplotで描画しやすいように、データを「ロングフォーマット」に変換
df_long <- df %>%
pivot_longer(
cols = -x,
names_to = "parameters",
values_to = "density"
) %>%
# 凡例の順序を調整
mutate(parameters = factor(parameters, levels = c(
"α=1 (平均なし)",
"α=2 (分散なし)",
"α=5 (分散あり)"
)))
# 4. 各分布に割り当てる色を定義
manual_colors <- c(
`α=1 (平均なし)` = "blue",
`α=2 (分散なし)` = "red",
`α=5 (分散あり)` = "darkgreen"
)
# 5. ggplotを使用してチャートを描画
p <- ggplot(df_long, aes(x = x, y = density, color = parameters)) +
geom_line(linewidth = 1.2) +
scale_color_manual(values = manual_colors) +
labs(
title = "形状パラメータ(α)によるフレシェ分布の変化",
subtitle = "αが小さいほど裾が重く、極端な値が出やすい",
x = "xの値",
y = "確率密度",
color = "形状パラメータ (α)"
) +
coord_cartesian(xlim = c(0, 8)) +
theme_minimal(base_size = 14) +
theme(
legend.position = "top",
plot.title = element_text(face = "bold"),
plot.subtitle = element_text(color = "gray40")
)
# チャートの表示
print(p)Figure 1 の解説
上記のRコードを実行すると、3つのフレシェ分布が描画されたチャート Figure 1 が生成されます。
-
α=1(青線): 形状パラメータが最も小さく、裾が最も重いケースです。ピークが左に寄っており、確率密度の減少が非常に緩やかです。 -
α=2(赤線): \(\alpha\)が大きくなったことで、分布のピークは右にシフトし、裾の減少が少し速くなっています。 -
α=5(緑線): 形状パラメータが最も大きく、裾が最も軽いケースです。分布はより中央に集中し、ピークはさらに右にシフトしています。
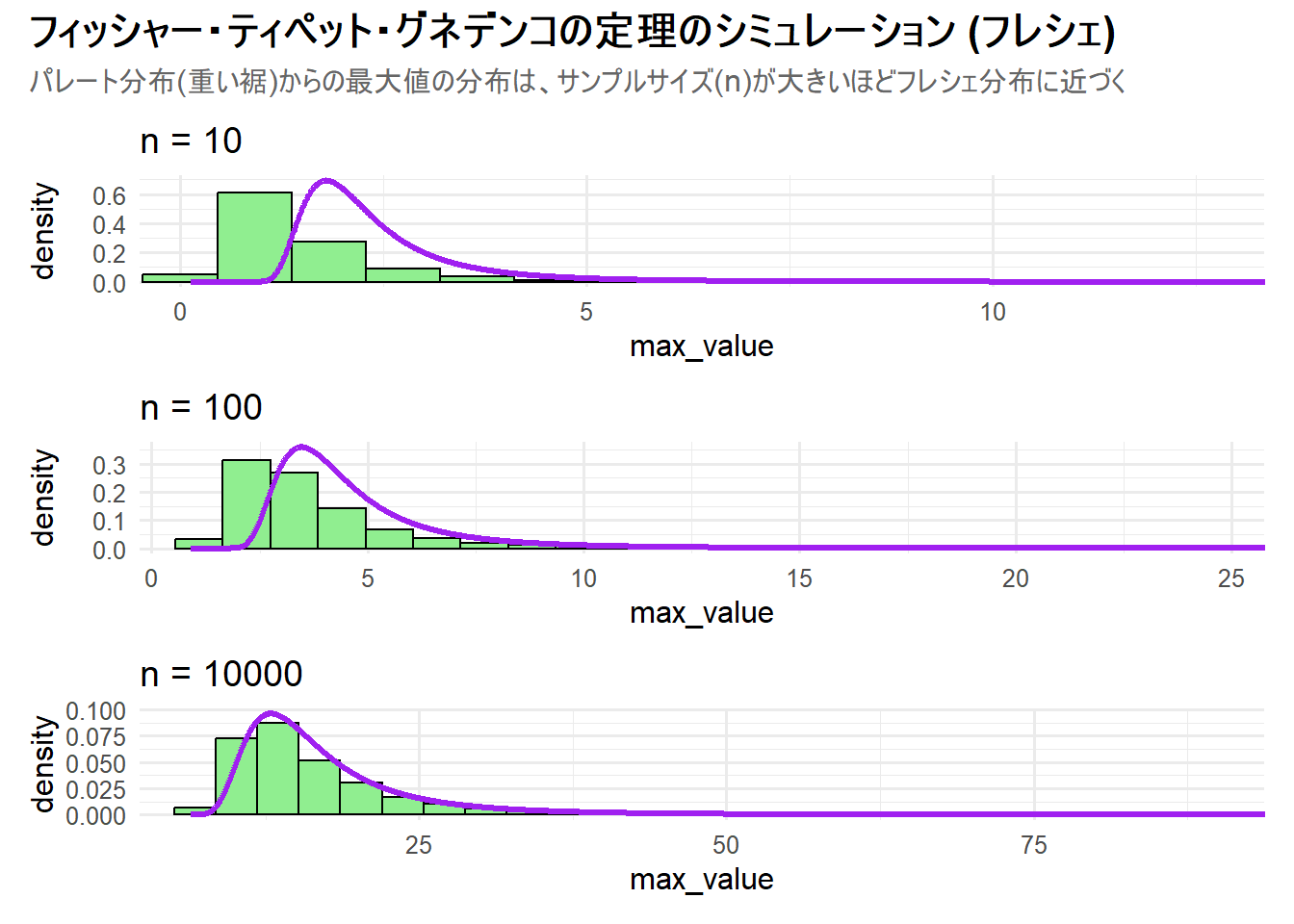
4. フィッシャー・ティペット・グネデンコの定理のシミュレーション
ここでは、定理の主張通り、裾が重い分布(今回はパレート分布)からサンプリングされた最大値の分布が、サンプルサイズを大きくするとフレシェ分布に収束することを確認します。
シミュレーションのステップ
- 元の分布: 形状パラメータ \(\alpha=3.5\) のパレート分布を選びます。
- サンプリング: パレート分布から \(n\) 個の乱数を1セットとし、その最大値を取り出します。これを10,000回繰り返します。
- 分布の確認: 集めた最大値の分布をヒストグラムで可視化し、理論的なフレシェ分布の曲線を重ねて比較します。
- サンプルサイズ \(n\) の影響: \(n=10, 100, 10000\) と変えて、収束の様子を観察します。
(注意):フレシェ分布への収束を見やすくするために、描画範囲を 99.9%タイル として、巨大な値を除外しています。
Rコード
# 必要なパッケージ
library(patchwork)
library(actuar)
# シミュレーションの設定
seed <- 20250808
set.seed(seed)
num_simulations <- 10000
sample_sizes <- c(10, 100, 10000)
pareto_alpha <- 3.5 # 元のパレート分布の形状パラメータ
# シミュレーションの実行
simulation_results_fr <- lapply(sample_sizes, function(n) {
# パレート分布(shape=3.5, scale=1)からn個サンプリングし、最大値を取得
max_values <- replicate(num_simulations, max(rpareto(n, shape = pareto_alpha, scale = 1)))
tibble(
n_val = n,
max_value = max_values
)
}) %>%
bind_rows()
# 理論的なフレシェ分布のパラメータを計算
# 元の分布がパレート(xm, α_p)の場合、最大値の分布は
# Frechet(shape = α_p, scale = xm*(n)^(1/α_p), loc = 0) で近似できる
frechet_params <- tibble(
n_val = sample_sizes
) %>%
mutate(
shape = pareto_alpha,
scale = (n_val)^(1 / pareto_alpha),
loc = 0 # loc=0ではなく、loc=scale となる場合もあるが、ここでは単純化
)
# 可視化
# 各サンプルサイズ(ファセット)に対応するプロットを個別に生成する関数
create_plot_for_n <- function(sample_n, sim_data, param_data) {
# 対象となるnのデータとパラメータを抽出
data_n <- sim_data %>% filter(n_val == sample_n)
params_n <- param_data %>% filter(n_val == sample_n)
# 描画範囲を決定 (99.9%タイル)して巨大な値を描画から除外。あくまでも描画のため。
plot_range <- quantile(data_n$max_value, c(0, 0.999))
# 個別のggplotオブジェクトを作成
p <- ggplot(data_n, aes(x = max_value)) +
geom_histogram(aes(y = after_stat(density)), bins = 50, fill = "lightgreen", color = "black") +
stat_function(
fun = dfrechet,
args = list(loc = params_n$loc, scale = params_n$scale, shape = params_n$shape),
aes(color = "理論値 (フレシェ分布)"),
linewidth = 1.2,
n = 5001
) +
# 描画範囲を個別に設定
coord_cartesian(xlim = plot_range) +
scale_color_manual(values = c("理論値 (フレシェ分布)" = "purple")) +
labs(title = paste("n =", sample_n)) +
theme_minimal(base_size = 12) +
theme(legend.position = "none") # 凡例は結合後に一つだけ表示
return(p)
}
# 各サンプルサイズでプロットを生成
plot_n10 <- create_plot_for_n(sample_sizes[1], simulation_results_fr, frechet_params)
plot_n100 <- create_plot_for_n(sample_sizes[2], simulation_results_fr, frechet_params)
plot_n10000 <- create_plot_for_n(sample_sizes[3], simulation_results_fr, frechet_params)
# patchworkを使ってプロットを結合
p_simulation_fr <- (plot_n10 / plot_n100 / plot_n10000) +
plot_layout(guides = "collect") + # 凡例をまとめる
plot_annotation(
title = "フィッシャー・ティペット・グネデンコの定理のシミュレーション (フレシェ)",
subtitle = "パレート分布(重い裾)からの最大値の分布は、サンプルサイズ(n)が大きいほどフレシェ分布に近づく",
theme = theme(
plot.title = element_text(face = "bold", size = 16),
plot.subtitle = element_text(color = "gray40", size = 12),
legend.position = "top"
)
)
# 最終的なチャートの表示
print(p_simulation_fr)Figure 2 の解説
上記のRコードを実行すると、3つのサンプルサイズにおける最大値の分布を可視化したチャート Figure 2 が生成されます。
-
n = 10(上段パネル): パレート分布から10個サンプリングした場合、その最大値の分布(ヒストグラム)は既に右に歪んだ形状をしていますが、理論的なフレシェ分布の曲線(紫色)からは離れています。 -
n = 100(中段パネル): サンプルサイズが100に増えると、最大値の分布全体が右にシフトしていますが、同じく理論曲線からは離れています。 -
n = 10000(下段パネル): サンプルサイズが10000になると、最大値の分布と理論的なフレシェ分布の曲線は、n=10、n=100の場合よりも、理論曲線に近くなっています。
以上です。