Rで確率分布:ベータ分布

Rで 確率分布:ベータ分布 を試みます。

本ポストはこちらの続きです。

const typesetMath = (el) => { if (window.MathJax) { // MathJax Typeset window.MathJax.typeset(); } else if (window.katex...

1. ベータ分布とは

ベータ分布（Beta Distribution）は、定義域が[0, 1]に限定された連続確率分布です。この特徴から、確率、割合、比率など、0から1の間の値をとる確率変数をモデル化するのに利用されます。

特に、ベイズ統計学の世界では、二項分布の成功確率 \(p\) に対する事前分布や事後分布として利用されます。

ベイズ統計における解釈（共役事前分布として）

ベータ分布のパラメータ \(\alpha, \beta\) は、ベイズ統計の文脈で直感的な意味を持ちます。コインの表が出る確率 \(p\) を推定する例で考えます。

まず、\(p\) の不確かさを事前分布 \(Beta(\alpha_{prior}, \beta_{prior})\) で表現します。
次に、コインを投げて「成功（表）が \(s\) 回、失敗（裏）が \(f\) 回」というデータを観測します。
すると、\(p\) の事後分布は、パラメータを単純に足し合わせるだけで更新でき、新しいベータ分布 \(Beta(\alpha_{prior}+s, \beta_{prior}+f)\) となります。

この更新則から、\(\alpha\) と \(\beta\) はしばしば「成功」と「失敗」の観測回数を数えるカウンターのようなものと解釈されます。例えば、情報がない状態を示す一様分布 \(Beta(1,1)\) を事前分布として用いた場合、事後分布は \(Beta(1+s, 1+f)\) となります。このため、「\(\alpha\) は成功回数+1、\(\beta\) は失敗回数+1」と解釈されます。

確率密度関数 (Probability Density Function, PDF)

ベータ分布に従う確率変数 \(X\) の確率密度関数 \(f(x)\) は、2つの正の形状パラメータ \(\alpha, \beta\) を用いて以下のように定義されます。

\[f(x | \alpha, \beta) = \dfrac{x^{\alpha-1}(1-x)^{\beta-1}}{B(\alpha, \beta)} \quad (0 \le x \le 1)\]

この関数は、2つのパラメータによってその形状が決定されます。

\(\alpha\) (アルファ): 形状パラメータ1 (shape1)
\(\beta\) (ベータ): 形状パラメータ2 (shape2)

式中の \(B(\alpha, \beta)\) はベータ関数と呼ばれ、確率密度関数の面積が1になるように調整する正規化定数です。\(B(\alpha, \beta) = \displaystyle\int_0^1 t^{\alpha-1}(1-t)^{\beta-1}dt\) で定義されます。

主な特徴

定義域: 確率変数は常に [0, 1] の範囲の値をとります。
形状の多様性: パラメータ \(\alpha, \beta\) の値によって、その形状は変化します。
- \(\alpha = \beta = 1\): 一様分布になります。
- \(\alpha = \beta > 1\): 0.5を中心とする左右対称な釣鐘型になります。
- \(\alpha > \beta > 1\): ピークが右に寄った（左に歪んだ）分布になります。
- \(\beta > \alpha > 1\): ピークが左に寄った（右に歪んだ）分布になります。
- \(\alpha, \beta < 1\): 両端が高くなるU字型の分布になります。
代表値:
- 平均 (Mean): \(E[X] = \dfrac{\alpha}{\alpha+\beta}\)
- 最頻値 (Mode): \(\dfrac{\alpha-1}{\alpha+\beta-2}\) （ただし、\(\alpha, \beta > 1\)の場合）
他の分布との関係:
- 一様分布: \(\alpha=1, \beta=1\) のベータ分布は、[0, 1]上の一様分布です。
- 順序統計量: [0, 1]の一様分布から得た \(n\) 個の標本のうち、\(k\) 番目に小さい値の分布は、\(\alpha=k, \beta=n-k+1\) のベータ分布に従います。

2. ベータ分布の応用例

その柔軟性と[0, 1]という定義域から、様々な分野で応用されます。

ベイズ統計学
- 例えば、「コインを10回投げて表が7回、裏が3回出た」というデータがあるとき、このコインの表が出る真の確率 \(p\) の事後分布は、事前分布にもよりますが、ベータ分布で表現できます。
A/Bテストの分析
- WebサイトのデザインAとBのクリック率（CVR）を比較する際に、各デザインのCVRの事後分布をベータ分布でモデル化し、AがBより優れている確率を直接計算することができます。
機械学習
- トピックモデル（LDA）: 文書中の単語の分布や、トピックの分布をモデル化する際に、その基盤としてベータ分布（多次元に拡張したディリクレ分布）が用いられます。
プロジェクト管理 (PERT法)
- あるタスクの完了時間を、楽観値(a), 最頻値(m), 悲観値(b)の3点で見積もり、それをベータ分布で近似して期待完了時間やリスクを評価する手法で利用されます。

3. R言語によるシミュレーション

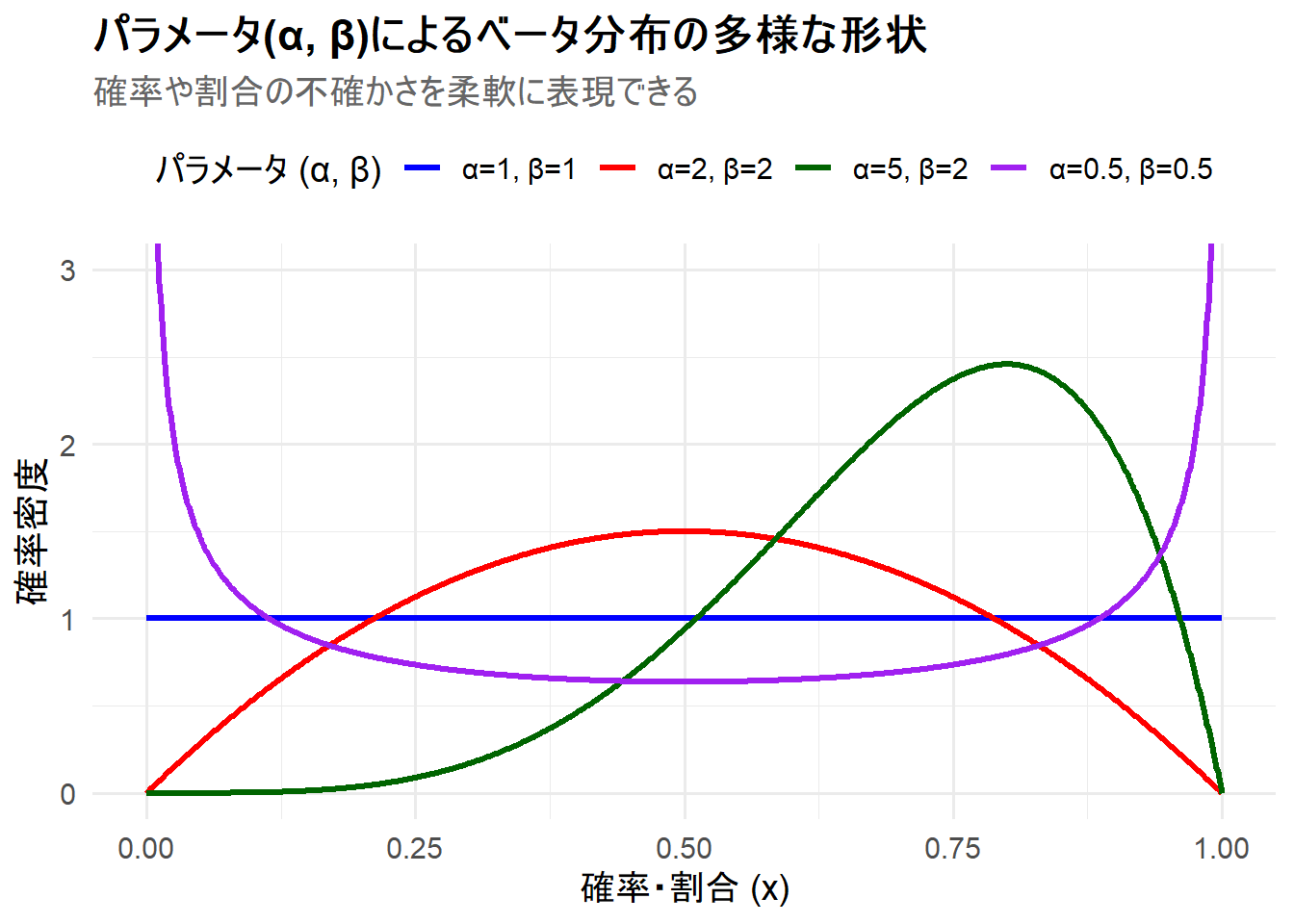
ここでは、形状パラメータ \(\alpha, \beta\) の組み合わせを変更した4つのベータ分布を1枚のチャートに描画します。これにより、ベータ分布がいかに多様な形状を表現できるかを視覚的に理解します。

ケース1: α=1, β=1 （一様分布）
ケース2: α=2, β=2 （対称な釣鐘型）
ケース3: α=5, β=2 （右に歪んだ（左に偏った）分布）
ケース4: α=0.5, β=0.5 （U字型の分布）

# 必要なライブラリを読み込みます
library(ggplot2)
library(dplyr)
library(tidyr)

# 1. 描画範囲となるx軸の値を生成
x_vals <- seq(0, 1, length.out = 1000)

# 2. 異なるパラメータを持つベータ分布の確率密度を計算
# dbeta(x, shape1, shape2) を使用。shape1がα, shape2がβ
df <- tibble(
  x = x_vals
) %>%
  mutate(
    `α=1, β=1` = dbeta(x, shape1 = 1, shape2 = 1),
    `α=2, β=2` = dbeta(x, shape1 = 2, shape2 = 2),
    `α=5, β=2` = dbeta(x, shape1 = 5, shape2 = 2),
    `α=0.5, β=0.5` = dbeta(x, shape1 = 0.5, shape2 = 0.5)
  )

# 3. ggplotで描画しやすいように、データを「ロングフォーマット」に変換
df_long <- df %>%
  pivot_longer(
    cols = -x,
    names_to = "parameters",
    values_to = "density"
  ) %>%
  # 凡例の順序を調整
  mutate(parameters = factor(parameters, levels = c(
    "α=1, β=1",
    "α=2, β=2",
    "α=5, β=2",
    "α=0.5, β=0.5"
  )))

# 4. 各分布に割り当てる色を定義
manual_colors <- c(
  `α=1, β=1` = "blue",
  `α=2, β=2` = "red",
  `α=5, β=2` = "darkgreen",
  `α=0.5, β=0.5` = "purple"
)

# 5. ggplotを使用してチャートを描画
p <- ggplot(df_long, aes(x = x, y = density, color = parameters)) +
  geom_line(linewidth = 1.2) +
  scale_color_manual(values = manual_colors) +
  labs(
    title = "パラメータ(α, β)によるベータ分布の多様な形状",
    subtitle = "確率や割合の不確かさを柔軟に表現できる",
    x = "確率・割合 (x)",
    y = "確率密度",
    color = "パラメータ (α, β)"
  ) +
  # U字型の分布を分かりやすくするため、y軸の範囲を調整
  coord_cartesian(ylim = c(0, 3.0)) +
  theme_minimal(base_size = 14) +
  theme(
    legend.position = "top",
    plot.title = element_text(face = "bold"),
    plot.subtitle = element_text(color = "gray40")
  )

# チャートの表示
print(p)

Figure 1 の解説

上記のRコードを実行すると、4つのベータ分布が描画されたチャート Figure 1 が生成されます。

α=1, β=1 (青線): 水平な直線となっており、これは[0, 1]区間における一様分布そのものです。これは「成功確率について全く情報がない」状態を表現するのに使われます。
α=2, β=2 (赤線): \(\alpha\)と\(\beta\)が等しいため、\(x=0.5\) を中心とする左右対称な釣鐘型の分布になっています。
α=5, β=2 (緑線): \(\alpha > \beta\) なので、分布のピークは右に寄っています（最頻値は(5-1)/(5+2-2)=0.8）。これは、例えば「成功が4回、失敗が1回観測された」後の成功確率の不確かさを表しており、確率が高い値である可能性がより高いことを示しています。
α=0.5, β=0.5 (紫線): \(\alpha\)と\(\beta\)が1未満のため、両端の確率密度が高くなるU字型の分布になっています。これは、確率が0か1に近い極端な値である可能性が高い、という信念を表現するのに使われます。

以上です。