Rで 確率分布:ポアソン分布 を試みます。
本ポストはこちらの続きです。

Rで確率分布:レヴィ分布
const typesetMath = (el) => { if (window.MathJax) { // MathJax Typeset window.MathJax.typeset(); } else if (window.katex...
1. ポアソン分布とは
ポアソン分布(Poisson Distribution)は、単位時間あたり、または単位空間あたりに、あるイベントが「稀に」発生する回数のモデル化に利用される代表的な離散確率分布です。
これまでに扱ってきた正規分布や指数分布などが連続的な値をとるのに対し、ポアソン分布が扱うのは「0回、1回、2回、…」といった整数値(カウントデータ)である点が大きな違いです。
確率質量関数 (Probability Mass Function, PMF)
離散確率分布では、確率密度関数(PDF)の代わりに確率質量関数(PMF)という用語を用います。これは、確率変数が特定の値 \(k\) をとる確率そのものを示します。
ポアソン分布に従う確率変数 \(X\) の確率質量関数 \(P(X=k)\) は、以下の式で定義されます。
\[P\left(X=k | \lambda\right) = \dfrac{\lambda^k e^{-\lambda}}{k!} \quad (k=0, 1, 2, \dots)\]
この分布は、ただ一つのパラメータによってその形状が決定されます。
- \(\lambda\): レートパラメータ (rate parameter)
- 単位時間(または単位空間)あたりにイベントが発生する平均回数を表します。
- この値が分布の形状と位置を決定します。
主な特徴
- 定義域: 確率変数がとりうる値は、0を含む非負の整数 (\(k=0, 1, 2, \dots\)) です。
- 形状:
- \(\lambda\) が小さいとき、分布は右に大きく歪んだ形状をしています。
- \(\lambda\) が大きくなるにつれて、分布の形状は左右対称な釣鐘型に近づき、正規分布でよく近似できるようになります。
- 代表値: ポアソン分布の特徴の1つは、平均と分散が等しくなることです。
- 平均 (Mean): \(E[X] = \lambda\)
- 分散 (Variance): \(V[X] = \lambda\)
- 他の分布との関係:
- 指数分布: 「単位時間あたりのイベント発生回数」がポアソン分布に従うとき、そのイベントの「発生間隔」は指数分布に従います。
- 二項分布: 試行回数 \(n\) が非常に大きく、成功確率 \(p\) が非常に小さい二項分布は、\(\lambda = np\) のポアソン分布で近似できます(ポアソンの少数の法則)。これは、非常に多くの試行の中で稀にしか起こらないイベントの回数をモデル化する理論的背景となります。
2. ポアソン分布の応用例
「単位あたりの発生回数」を数える様々な場面で応用されます。
- 時間的な応用
- 1時間にあるウェブサイトへ届くアクセス数
- 1日に特定の交差点で発生する交通事故の件数
- 1分間に銀行の窓口に訪れる顧客の数
- 1年間に特定の地域に雷が落ちる回数
- 空間的な応用
- 1平方メートルのガラス板に含まれる傷の数
- 1ページの文章に含まれる誤植の数
- 1リットルの水に含まれる特定のバクテリアの数
- その他
- 1試合におけるサッカーチームの総得点数
- 1個のパン生地に含まれるレーズンの数
3. R言語によるシミュレーション
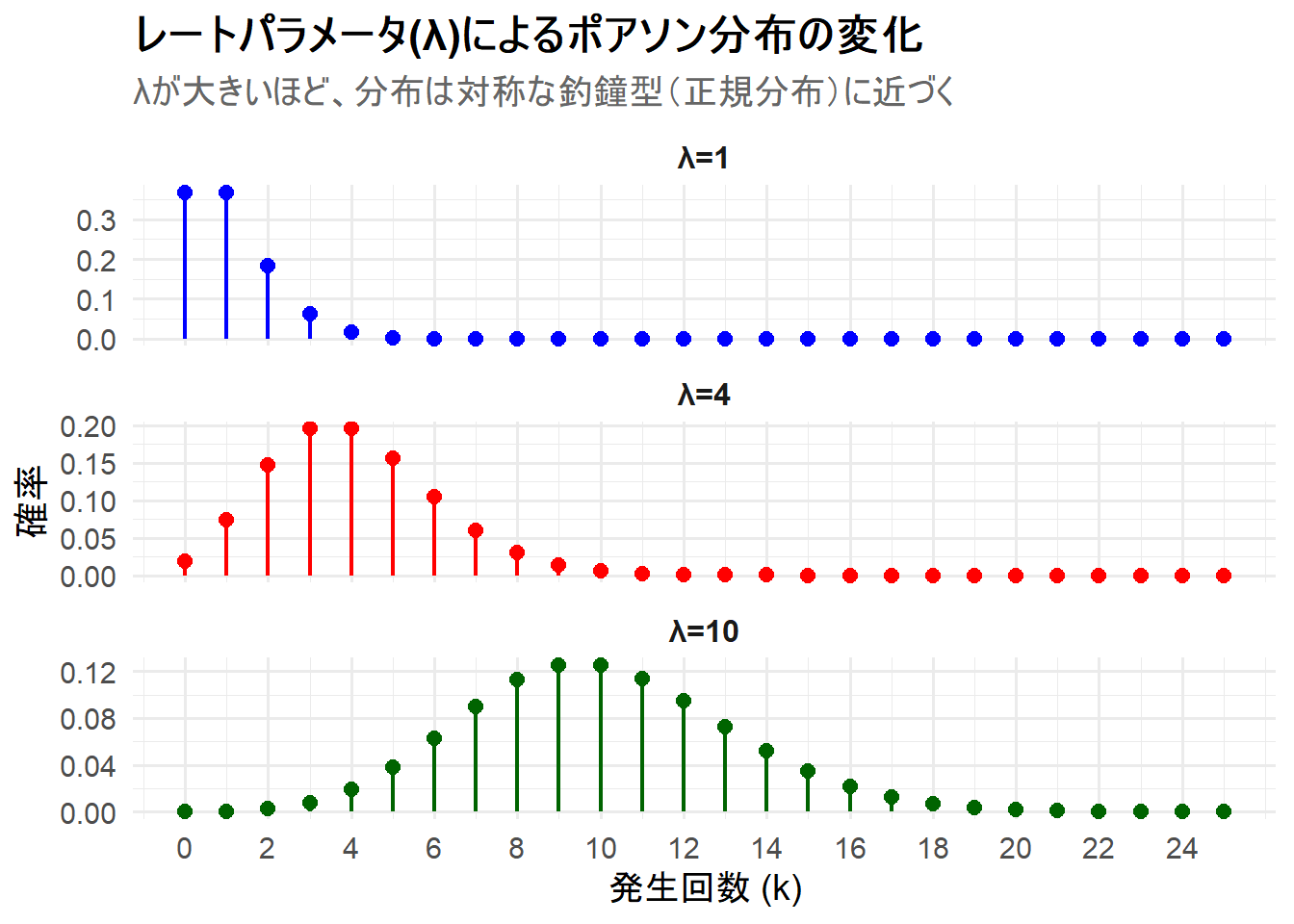
ここでは、レートパラメータ \(\lambda\) を変更した3つのポアソン分布を1枚のチャートに描画します。ポアソン分布は離散分布であるため、グラフはロリポップチャート(点と線)で表現し、特定の値しかとらないことを視覚的に明確にします。
- ケース1:
λ=1(右に大きく歪んだ形状) - ケース2:
λ=4(歪みが小さくなる) - ケース3:
λ=10(正規分布に近い、対称な釣鐘型)
Rコード
# 必要なライブラリを読み込みます
library(ggplot2)
library(dplyr)
library(tidyr)
# 1. 描画範囲となるx軸の値(整数)を生成
k_vals <- 0:25
# 2. 異なるレートパラメータを持つポアソン分布の確率質量を計算
# dpois(k, lambda) を使用
df <- tibble(
k = k_vals
) %>%
mutate(
`λ=1` = dpois(k, lambda = 1),
`λ=4` = dpois(k, lambda = 4),
`λ=10` = dpois(k, lambda = 10)
)
# 3. ggplotで描画しやすいように、データを「ロングフォーマット」に変換
df_long <- df %>%
pivot_longer(
cols = -k,
names_to = "parameters",
values_to = "probability"
) %>%
# 凡例の順序を調整
mutate(parameters = factor(parameters, levels = c(
"λ=1",
"λ=4",
"λ=10"
)))
# 4. 各分布に割り当てる色を定義
manual_colors <- c(
`λ=1` = "blue",
`λ=4` = "red",
`λ=10` = "darkgreen"
)
# 5. ggplotを使用してチャートを描画(ファセットで分割)
p <- ggplot(df_long, aes(x = k, y = probability, color = parameters)) +
# 離散分布を表現するために、点と線(ロリポップ)を使う
geom_segment(aes(xend = k, yend = 0), linewidth = 0.8) +
geom_point(size = 2.5) +
# ケースごとにプロットを分割
facet_wrap(~parameters, ncol = 1, scales = "free_y") +
scale_color_manual(values = manual_colors) +
labs(
title = "レートパラメータ(λ)によるポアソン分布の変化",
subtitle = "λが大きいほど、分布は対称な釣鐘型(正規分布)に近づく",
x = "発生回数 (k)",
y = "確率"
) +
scale_x_continuous(breaks = seq(0, 25, by = 2)) + # x軸の目盛りを調整
theme_minimal(base_size = 14) +
theme(
legend.position = "none", # ファセットで分けているので凡例は不要
plot.title = element_text(face = "bold"),
plot.subtitle = element_text(color = "gray40"),
strip.text = element_text(face = "bold", size = 12) # ファセットのラベルを調整
)
# チャートの表示
print(p)Figure 1 の解説
上記のRコードを実行すると、3つのポアソン分布が描画されたチャート Figure 1 が生成されます。
-
λ=1(上段): 平均発生回数が1回の場合です。0回や1回となる確率が最も高く、分布は右に大きく歪んでいます。 -
λ=4(中段): 平均発生回数が4回になると、分布のピークは \(k=3, 4\) のあたりに移動し、歪みが小さくなってきているのがわかります。 -
λ=10(下段): 平均発生回数が10回になると、分布は \(k=10\) を中心とした、かなり左右対称な釣鐘型の形状になっています。これは、正規分布で近似できることを示唆しています。
以上です。