Rで 確率分布:ラプラス分布 を試みます。
本ポストはこちらの続きです。

Rで確率分布:ベータ分布
const typesetMath = (el) => { if (window.MathJax) { // MathJax Typeset window.MathJax.typeset(); } else if (window.katex...
1. ラプラス分布とは
ラプラス分布(Laplace Distribution)は、両側指数分布(Double Exponential Distribution)とも呼ばれ、正規分布とよく似た左右対称な釣鐘型の確率分布です。しかし、その特徴は、分布の中心(平均)で鋭く尖ったピークを持ち、正規分布よりも裾が重い(fat-tailed)点にあります。
この「尖ったピーク」と「重い裾」という性質から、外れ値に対してより頑健なモデリングや、機械学習におけるLasso回帰の理論的背景として利用されます。
確率密度関数 (Probability Density Function, PDF)
ラプラス分布に従う確率変数 \(X\) の確率密度関数 \(f(x)\) は、2つのパラメータを用いて以下のように定義されます。
\[f\left(x | \mu, b\right) = \dfrac{1}{2b} \exp\left(-\dfrac{|x-\mu|}{b}\right)\]
この分布は、2つのパラメータによってその形状が決定されます。
- \(\mu\) : 位置パラメータ (location parameter)
- 分布の中心の位置を決定します。正規分布の平均と同様の役割です。
- ラプラス分布では、平均、中央値、最頻値がすべて一致し、\(\mu\) となります。
- \(b\) : 尺度パラメータ (scale parameter)
- 分布の広がり(ばらつき)を決定する正のパラメータです。正規分布の標準偏差に似た役割を果たします。
- \(b\) が大きいほど、分布は広く平たくなります。
主な特徴
- 形状: 平均 \(\mu\) を中心に左右対称ですが、正規分布の滑らかな釣鐘型とは異なり、\(\mu\)で鋭く尖った山の形をしています。
- 裾の重さ (Fat Tails): 正規分布の確率は裾の部分で急速に0に近づきますが、ラプラス分布は指数的に減少するため、相対的に緩やかに減少します。これにより、平均から大きく離れた値(外れ値)が出現する確率が正規分布よりも高くなります。
- 代表値:
- 平均 (Mean): \(E[X] = \mu\)
- 分散 (Variance): \(V[X] = 2b^2\)
- 指数分布との関係: ラプラス分布は、2つの同じ指数分布を背中合わせにした形をしています。レートパラメータが \(\lambda=1/b\) の指数分布に従う確率変数を \(Y\) とすると、\(Y\) と \(-Y\) の確率的な混合としてラプラス分布を考えることができます。このことから「両側指数分布」と呼ばれます。
2. ラプラス分布の応用例
ラプラス分布の特性は、特に機械学習とロバスト統計の分野で利用されます。
- Lasso回帰(L1正則化)
- ベイズ統計の観点から見ると、回帰モデルの係数にラプラス分布を事前分布として仮定することは、Lasso回帰を行うことと等価です。ラプラス分布が原点(0)で鋭く尖っている性質が、多くの係数を厳密に0にするスパース性(不要な変数を選択的に除く効果)を生み出す理論的な根拠となっています。
- ロバスト統計
- データの誤差が正規分布に従うと仮定する最小二乗法は、外れ値に弱いという欠点があります。一方で、誤差にラプラス分布を仮定する最尤推定は、最小絶対偏差(LAD)回帰と等価になります。ラプラス分布は裾が重いため、外れ値の影響を受けにくく、より頑健(ロバスト)な推定が可能になります。
- 信号処理・画像処理
- 自然画像の差分信号や、特定の音声信号の特徴量など、多くの実世界の信号が、正規分布よりもラプラス分布によく適合することが知られています。
3. R言語によるシミュレーション
ここでは、ラプラス分布のパラメータを変更した3つのケースと、比較対象として同じ平均・分散を持つ正規分布を1枚のチャートに描画します。これにより、パラメータの効果と、正規分布との本質的な違い(ピークの尖り、裾の重さ)を視覚的に理解します。
- ケース1: ラプラス分布
μ=0, b=1 - ケース2: ラプラス分布
μ=5, b=1(位置をシフト) - ケース3: ラプラス分布
μ=0, b=2(尺度を広げる) - ケース4: 正規分布
μ=0, σ=√2(ケース1と同じ平均・分散を持つ正規分布)
# 必要なライブラリを読み込みます
library(ggplot2)
library(dplyr)
library(tidyr)
# ラプラス分布の確率密度関数(PDF)を定義
d_laplace <- function(x, mu, b) {
1 / (2 * b) * exp(-abs(x - mu) / b)
}
# 1. 描画範囲となるx軸の値を生成
x_vals <- seq(-8, 12, length.out = 1000)
# 2. 異なるパラメータを持つ分布の確率密度を計算
# ラプラス分布(μ=0, b=1)の分散は 2*b^2 = 2。
# よって比較対象の正規分布の標準偏差は sqrt(2)
b1_var <- 2 * 1^2
norm_sd <- sqrt(b1_var)
df <- tibble(
x = x_vals
) %>%
mutate(
`ラプラス (μ=0, b=1)` = d_laplace(x, mu = 0, b = 1),
`ラプラス (μ=5, b=1)` = d_laplace(x, mu = 5, b = 1),
`ラプラス (μ=0, b=2)` = d_laplace(x, mu = 0, b = 2),
`正規分布 (μ=0, σ=√2)` = dnorm(x, mean = 0, sd = norm_sd)
)
# 3. ggplotで描画しやすいように、データを「ロングフォーマット」に変換
df_long <- df %>%
pivot_longer(
cols = -x,
names_to = "distribution",
values_to = "density"
) %>%
# 凡例の順序を調整
mutate(distribution = factor(distribution, levels = c(
"ラプラス (μ=0, b=1)",
"ラプラス (μ=5, b=1)",
"ラプラス (μ=0, b=2)",
"正規分布 (μ=0, σ=√2)"
)))
# 4. 各分布に割り当てる色と線種を定義
manual_colors <- c(
`ラプラス (μ=0, b=1)` = "blue",
`ラプラス (μ=5, b=1)` = "red",
`ラプラス (μ=0, b=2)` = "darkgreen",
`正規分布 (μ=0, σ=√2)` = "black"
)
manual_linetypes <- c(
`ラプラス (μ=0, b=1)` = "solid",
`ラプラス (μ=5, b=1)` = "solid",
`ラプラス (μ=0, b=2)` = "solid",
`正規分布 (μ=0, σ=√2)` = "dashed"
)
# 5. ggplotを使用してチャートを描画
p <- ggplot(df_long, aes(x = x, y = density, color = distribution, linetype = distribution)) +
geom_line(linewidth = 1.2) +
scale_color_manual(values = manual_colors) +
scale_linetype_manual(values = manual_linetypes) +
labs(
title = "ラプラス分布の変化と正規分布との比較",
subtitle = "正規分布に比べピークが鋭く、裾が重いのが特徴",
x = "xの値",
y = "確率密度",
color = "分布の種類",
linetype = "分布の種類"
) +
theme_minimal(base_size = 14) +
theme(
legend.position = "top",
plot.title = element_text(face = "bold"),
plot.subtitle = element_text(color = "gray40")
) +
guides(color = guide_legend(nrow = 2))
# チャートの表示
print(p)
p_log <- ggplot(df_long, aes(x = x, y = density, color = distribution, linetype = distribution)) +
geom_line(linewidth = 1.2) +
# 対数スケールに変更するレイヤーを追加。ただしdensity=0はプロットできないので、非常に小さい値をクリップ
scale_y_log10(
breaks = scales::trans_breaks("log10", function(x) 10^x),
labels = scales::trans_format("log10", scales::math_format(10^.x))
) +
scale_color_manual(values = manual_colors) +
scale_linetype_manual(values = manual_linetypes) +
labs(
title = "ラプラス分布と正規分布の比較(y軸対数スケール)",
subtitle = "対数スケールにしてラプラス分布の裾の重さ(減少の遅さ)を明確化",
x = "xの値",
y = "確率密度 (対数スケール)",
color = "分布の種類",
linetype = "分布の種類"
) +
# y軸の表示範囲を指定。下限を10^-10に設定
coord_cartesian(xlim = c(-8, 8), ylim = c(1e-10, NA)) + # NAは上限を自動設定
theme_minimal(base_size = 14) +
theme(
legend.position = "top",
plot.title = element_text(face = "bold"),
plot.subtitle = element_text(color = "gray40")
) +
guides(color = guide_legend(nrow = 2))
# 対数スケールのチャートを表示
print(p_log)Figure 1,Figure 2 の解説
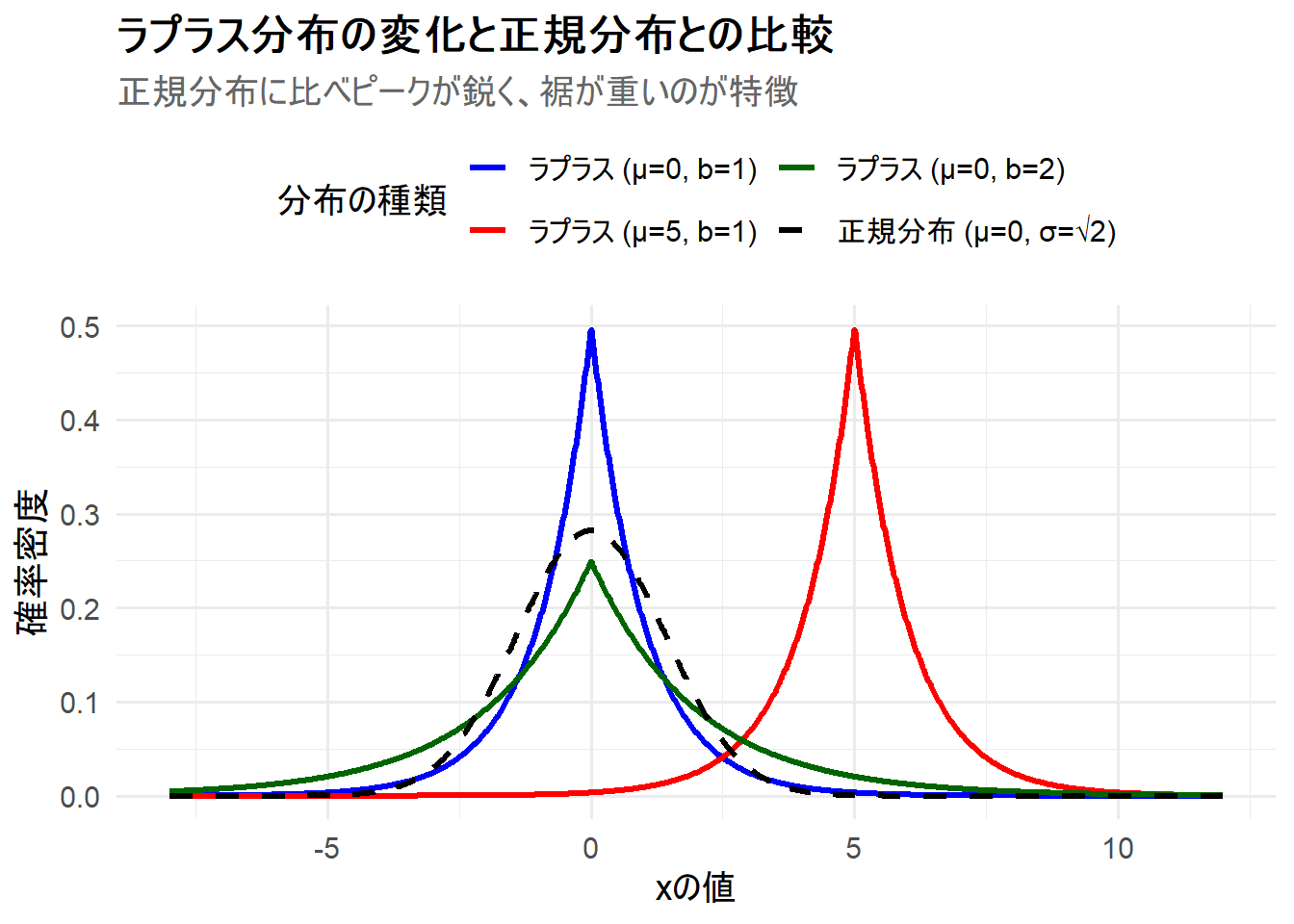
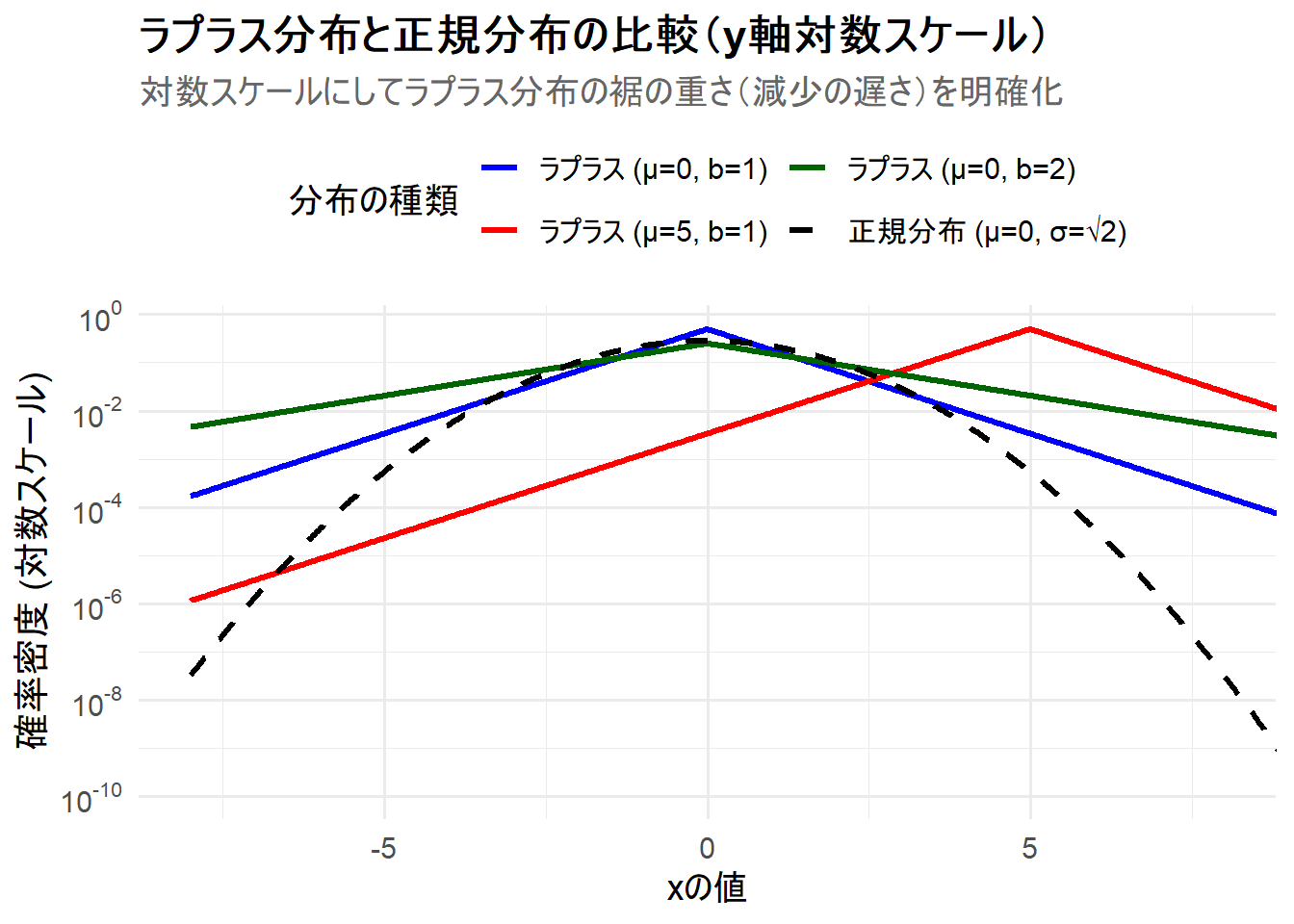
上記のRコードを実行すると、3つのラプラス分布と1つの正規分布が描画されたチャート Figure 1,Figure 2 が生成されます。
-
ラプラス (μ=0, b=1)(青線): 基準となる標準的なラプラス分布です。\(x=0\)で鋭く尖ったピークを持っています。 -
ラプラス (μ=5, b=1)(赤線): 位置パラメータ \(\mu\) を5にしたことで、青線の分布がそのまま右に5だけ平行移動しています。 -
ラプラス (μ=0, b=2)(緑線): 尺度パラメータ \(b\) を2倍にしたことで、青線と比べて分布が広く、平たくなっています。 -
正規分布 (μ=0, σ=√2)(黒破線): 青線のラプラス分布と同じ平均(0)と分散(2)を持つ正規分布です。両者を比較すると、ラプラス分布の際立った特徴がわかります。- ピーク: ラプラス分布(青線)は中心(\(x=0\))でより鋭く尖っているのに対し、正規分布(黒破線)は滑らかな丸い山型です。
- 裾: \(x\)が中心から離れると(例: \(|x|>5\))、ラプラス分布の裾は正規分布の裾よりも上側にあり、確率密度がより高いことがわかります。これが「裾が重い」ことを意味し、外れ値が発生する確率がより高いことを示唆しています。
以上です。