Rで 確率分布:レヴィ分布 を試みます。
本ポストはこちらの続きです。

1. レヴィ分布とは
レヴィ分布(Lévy Distribution)は、フランスの数学者ポール・レヴィにちなんで名付けられた連続確率分布です。これは、より広いクラスである安定分布(Stable Distribution)の特殊なケースであり、特に正規分布とコーシー分布と同じく、唯一確率密度関数が陽な形で記述できる安定分布の一つとして知られています(ただし、標準レヴィ分布の形)。
レヴィ分布の最大の特徴は、非常に重い裾(ヘビーテール)を持つことです。これにより、正規分布では捉えきれないような極端な外れ値が頻繁に発生する現象のモデリングに利用されます。また、定義域が下限を持つという点も特徴的です。
確率密度関数 (Probability Density Function, PDF)
レヴィ分布に従う確率変数 \(X\) の確率密度関数 \(f(x)\) は、2つのパラメータを用いて以下のように定義されます。
\[f\left(x | \mu, c\right) = \sqrt{\dfrac{c}{2\pi}} \dfrac{1}{\left(x-\mu\right)^{3/2}} \exp\left(-\dfrac{c}{2\left(x-\mu\right)}\right) \quad (x > \mu)\]
この分布は、2つのパラメータによってその形状が決定されます。
- \(\mu\): 位置パラメータ (location parameter)
- 分布の下限(最も小さい値)を決定します。確率変数 \(X\) は常に \(\mu\) より大きい値をとります。
- \(c\): 尺度パラメータ (scale parameter)
- 分布の広がりを決定する正のパラメータです。この値が小さいほど、分布のピークは高くなり、中心に集中する傾向が強くなります。
主な特徴
- 定義域: 確率変数は、位置パラメータ \(\mu\) より大きい値 (\(x > \mu\)) をとります。
- 形状: \(\mu\) から始まり、右に大きく歪んだ(裾を引く)形状をしています。\(\mu\) に近いほど確率密度は高くなりますが、厳密なピークの位置は \(x = \mu + c/3\) となります。
- 平均・分散が存在しない: コーシー分布と同様に、レヴィ分布は裾が極端に重いため、平均や分散といったモーメントが存在しません(無限大に発散します)。これは、この分布に従うデータにおいて、極端な外れ値が頻繁に発生し、データの中心やばらつきを一般的な方法で定義することが難しいことを意味します。
2. レヴィ分布の応用例
その裾の重さから、通常の正規分布などでは表現しきれない「大きなジャンプ」や「突然の大きな変動」を伴う現象のモデリングに利用されます。
- 金融市場
- 株価や為替レートの変動(リターン)をモデル化する際に、市場の暴落や急騰といった大きな価格ジャンプを捉えるために利用されることがあります。通常のブラウン運動に基づくモデルでは捉えきれない、現実の市場が持つ「肥沃な裾」を表現できます。
- 物理学
- 異常拡散(Anomalous Diffusion): 粒子のランダムウォークにおいて、通常の拡散(正規分布でモデル化される)よりもはるかに長いステップを時折踏むような現象(レヴィ・フライト)のモデリングに用いられます。生物の探索行動(例:鳥や昆虫の動き)にもレヴィ・フライトが見られることがあります。
- ブラックスワン現象: 予測不能な極端な事象の発生確率を、より現実的に評価する理論的背景となることがあります。
- 信号処理
- ノイズが正規分布ではなく、偶発的に非常に大きな値をとる(インパルス性ノイズ)ような状況で、信号のフィルタリングなどに適用されることがあります。
3. R言語によるシミュレーション
ここでは、位置パラメータ \(\mu\) と尺度パラメータ \(c\) を変更した3つのレヴィ分布を1枚のチャートに描画します。
- ケース1:
μ=0, c=1(標準的なレヴィ分布) - ケース2:
μ=2, c=1(位置をシフト) - ケース3:
μ=0, c=2(尺度を広げる)
Rコード
# 必要なライブラリを読み込みます
library(ggplot2)
library(dplyr)
library(tidyr)
library(rmutil) # 関数dlevyを利用
# 1. 描画範囲となるx軸の値を生成
x_vals <- seq(0, 10, length.out = 1000)
# 2. 異なるパラメータを持つレヴィ分布の確率密度を計算
df <- tibble(
x = x_vals
) %>%
mutate(
# μ=0, c=1 の場合 (m=0)
`μ=0, c=1` = {
# 1. 結果を格納するベクトルを0で初期化
res <- numeric(length(x))
# 2. 条件を満たすデータの位置を特定
idx <- x > 0
# 3. 条件を満たすデータだけで計算し、結果を代入
res[idx] <- dlevy(y = x[idx], m = 0, s = 1)
# 最終的な結果ベクトルを返す
res
},
# μ=2, c=1 の場合 (m=2)
`μ=2, c=1` = {
res <- numeric(length(x))
idx <- x > 2
# x[idx]が空でない場合のみ計算する
if (any(idx)) {
res[idx] <- dlevy(y = x[idx], m = 2, s = 1)
}
res
},
# μ=0, c=2 の場合 (m=0)
`μ=0, c=2` = {
res <- numeric(length(x))
idx <- x > 0
res[idx] <- dlevy(y = x[idx], m = 0, s = 2)
res
}
)
# 3. ggplotで描画しやすいように、データを「ロングフォーマット」に変換
df_long <- df %>%
pivot_longer(
cols = -x,
names_to = "parameters",
values_to = "density"
) %>%
# 凡例の順序を調整
mutate(parameters = factor(parameters, levels = c(
"μ=0, c=1",
"μ=2, c=1",
"μ=0, c=2"
)))
# 4. 各分布に割り当てる色を定義
manual_colors <- c(
`μ=0, c=1` = "blue",
`μ=2, c=1` = "red",
`μ=0, c=2` = "darkgreen"
)
# 5. ggplotを使用してチャートを描画
p <- ggplot(df_long, aes(x = x, y = density, color = parameters)) +
# 密度がNAになる部分(定義域外)はプロットしない
geom_line(data = . %>% filter(!is.na(density) & density > 1e-10), linewidth = 1.2) + # y軸0対応
scale_color_manual(values = manual_colors) +
labs(
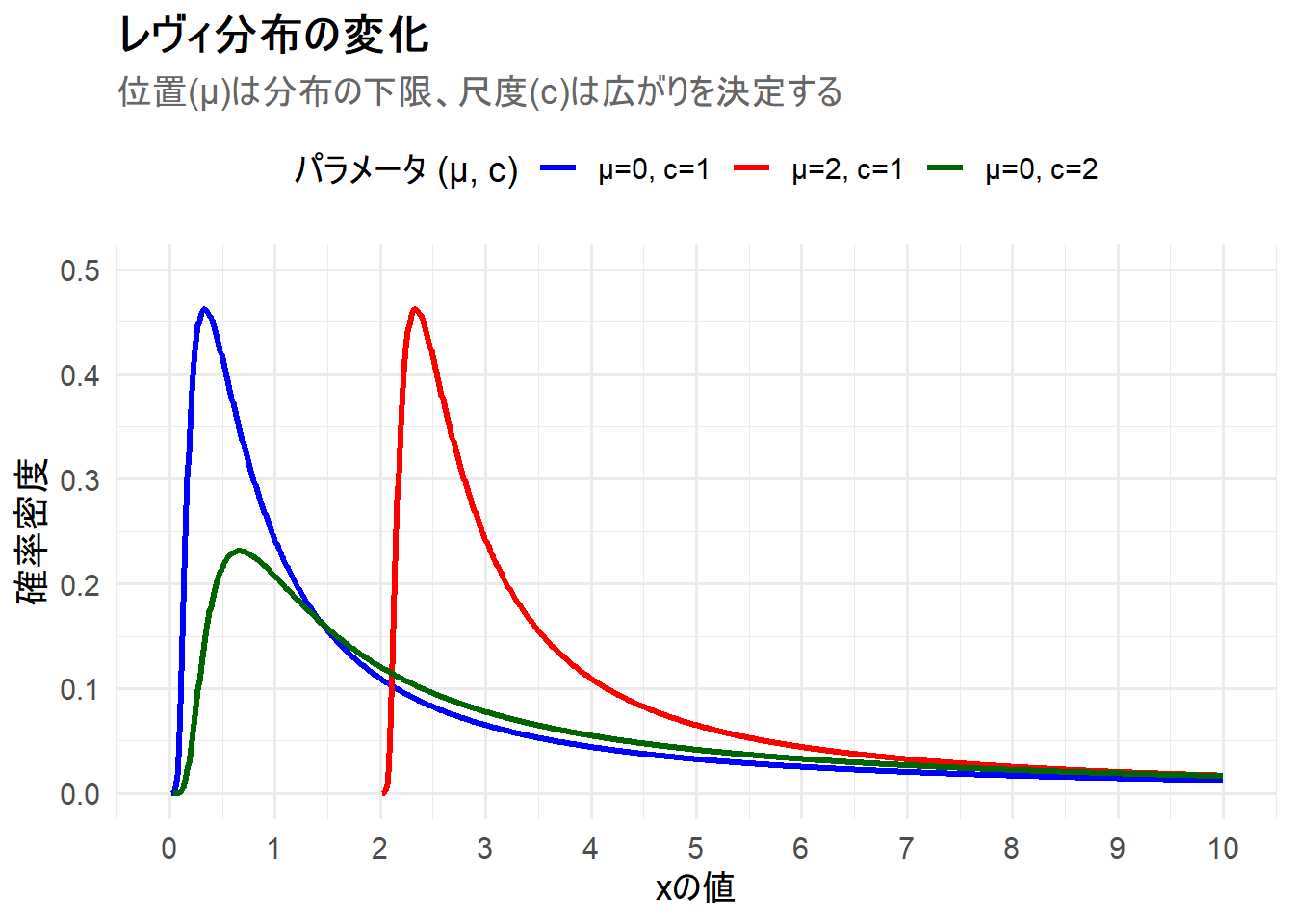
title = "レヴィ分布の変化",
subtitle = "位置(μ)は分布の下限、尺度(c)は広がりを決定する",
x = "xの値",
y = "確率密度",
color = "パラメータ (μ, c)"
) +
coord_cartesian(xlim = c(0, 10), ylim = c(0, 0.5)) + # 見やすい範囲に調整
theme_minimal(base_size = 14) +
theme(
legend.position = "top",
plot.title = element_text(face = "bold"),
plot.subtitle = element_text(color = "gray40")
) +
scale_x_continuous(breaks = scales::pretty_breaks(10))
# チャートの表示
print(p)Figure 1 の解説
上記のRコードを実行すると、3つのレヴィ分布が描画されたチャート Figure 1 が生成されます。
-
μ=0, c=1(青線): 基準となるレヴィ分布です。\(x=0\)から始まり、右に大きく歪んだ(裾を引く)形状をしています。ピークは\(x=c/3=1/3 \approx 0.33\)のあたりにあります。 -
μ=2, c=1(赤線): 位置パラメータ \(\mu\) を2にシフトしたケースです。青線と全く同じ形状の分布が、全体として右に2だけ平行移動し、\(x=2\)から始まっていることがわかります。 -
μ=0, c=2(緑線): 尺度パラメータ \(c\) を2倍にしたケースです。青線と比べて分布が右に広がり、ピークが低くなっています。これは、より大きな値が出現する可能性が高まる(ばらつきが大きくなる)ことを示しています。
以上です。