Rで 確率分布:ロジスティック分布 を試みます。
本ポストはこちらの続きです。

1. ロジスティック分布とは
ロジスティック分布(Logistic Distribution)は、正規分布とよく似た、左右対称な釣鐘型の連続確率分布です。その最大の特徴は、累積分布関数(CDF)がロジスティック関数(シグモイド関数)という単純で扱いやすい数式で表現できる点にあります。
この性質から、確率や割合のモデリング、特にロジスティック回帰分析の理論的な基礎として、統計学や機械学習の分野で重要な役割を果たしています。
確率密度関数 (PDF) と累積分布関数 (CDF)
ロジスティック分布に従う確率変数 \(X\) の確率密度関数 (PDF) \(f(x)\) は、2つのパラメータを用いて以下のように定義されます。
\[f\left(x | \mu, s\right) = \dfrac{e^{-(x-\mu)/s}}{s\left(1+e^{-(x-\mu)/s}\right)^2}\]
そして、累積分布関数 (CDF) \(F(x)\) は、以下のようになります。
\[F\left(x | \mu, s\right) = P(X \le x) = \dfrac{1}{1+e^{-(x-\mu)/s}}\]
このCDFの形が、S字カーブを描くロジスティック関数(シグモイド関数)そのものです。
この分布は、2つのパラメータによってその形状が決定されます。
- \(\mu\): 位置パラメータ (location parameter)
- 分布の中心の位置を決定します。これは分布の平均、中央値、最頻値と一致します。
- \(s\): 尺度パラメータ (scale parameter)
- 分布の広がり(ばらつき)を決定する正のパラメータです。この値が大きいほど、分布は広く平たくなります。
主な特徴
- 形状: 平均 \(\mu\) を中心に左右対称な釣鐘型をしており、正規分布に似ています。
- 裾の重さ (Fat Tails): 正規分布と比較すると、中心のピークが尖っており、その分、裾がわずかに重いという特徴があります。ラプラス分布やコーシー分布ほどではありませんが、正規分布よりは外れ値が出やすい性質を持ちます。
- 代表値:
- 平均 (Mean): \(E[X] = \mu\)
- 分散 (Variance): \(V[X] = \dfrac{\pi^2 s^2}{3}\)
- CDFの利便性: CDFが解析的に簡単な形で書けるため、確率の計算や逆関数(クォンタイル関数)の導出が容易であるという実用上の大きな利点があります。
2. ロジスティック分布の応用例
そのCDFの特性から、確率のモデリングに広く応用されます。
- ロジスティック回帰分析
- ある事象が発生する「確率」を、説明変数を用いて予測する際に用いられます。例えば、年齢や収入から、ある商品を購入する確率を予測するモデルなどです。モデルの出力(確率)が必ず0から1の間に収まるように、ロジスティック関数(ロジスティック分布のCDF)がリンク関数として利用されます。
- 生存時間分析
- 特定のイベントが発生するまでの時間を分析する際に、比例ハザードモデルなどで利用されることがあります。
- レーティングシステム
- チェスや囲碁などのプレイヤーの実力を評価するEloレーティングシステムでは、2人のプレイヤー間の勝率を予測する際に、実力差をロジスティック分布のCDFに入力して計算します。
3. R言語によるシミュレーション
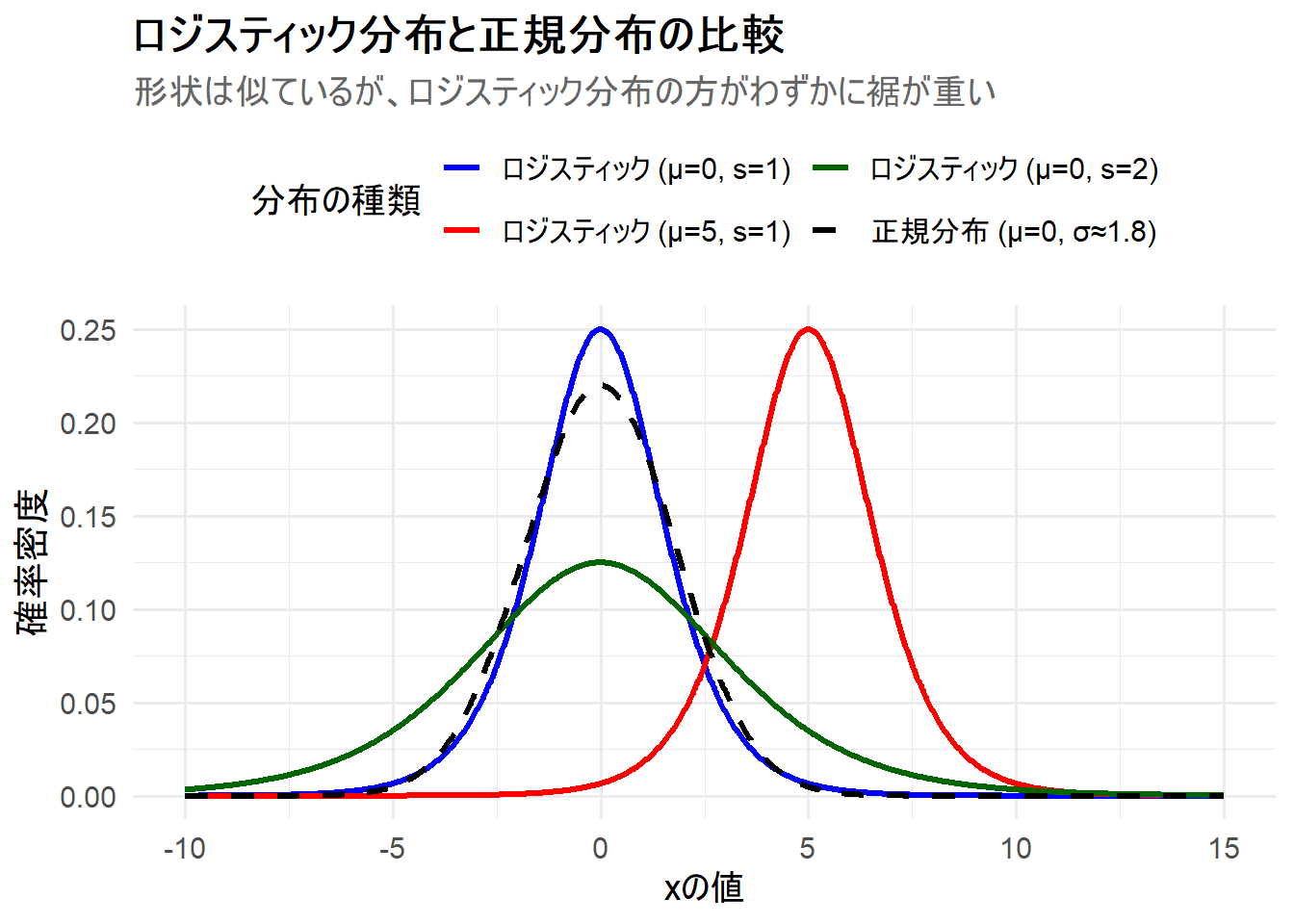
ここでは、ロジスティック分布のパラメータを変更した3つのケースと、比較対象として同じ平均・分散を持つ正規分布を1枚のチャートに描画します。これにより、ロジスティック分布と正規分布が視覚的に似ていること、そしてその微妙な違いを理解します。
- ケース1: ロジスティック分布
μ=0, s=1(標準ロジスティック分布) - ケース2: ロジスティック分布
μ=5, s=1(位置をシフト) - ケース3: ロジスティック分布
μ=0, s=2(尺度を広げる) - 比較対象: 正規分布 (ケース1と同じ平均・分散を持つ正規分布)
Rコード
# 必要なライブラリを読み込みます
library(ggplot2)
library(dplyr)
library(tidyr)
# 1. 描画範囲となるx軸の値を生成
x_vals <- seq(-10, 15, length.out = 1000)
# 2. 異なるパラメータを持つ分布の確率密度を計算
# ロジスティック分布は dlogis(x, location, scale) を使用
# 標準ロジスティック(μ=0, s=1)の分散は (pi^2 * 1^2)/3
logis_var <- (pi^2 * 1^2) / 3
norm_sd <- sqrt(logis_var) # 対応する正規分布の標準偏差
df <- tibble(
x = x_vals
) %>%
mutate(
`ロジスティック (μ=0, s=1)` = dlogis(x, location = 0, scale = 1),
`ロジスティック (μ=5, s=1)` = dlogis(x, location = 5, scale = 1),
`ロジスティック (μ=0, s=2)` = dlogis(x, location = 0, scale = 2),
`正規分布 (μ=0, σ≈1.8)` = dnorm(x, mean = 0, sd = norm_sd)
)
# 3. ggplotで描画しやすいように、データを「ロングフォーマット」に変換
df_long <- df %>%
pivot_longer(
cols = -x,
names_to = "distribution",
values_to = "density"
) %>%
# 凡例の順序を調整
mutate(distribution = factor(distribution, levels = c(
"ロジスティック (μ=0, s=1)",
"ロジスティック (μ=5, s=1)",
"ロジスティック (μ=0, s=2)",
"正規分布 (μ=0, σ≈1.8)"
)))
# 4. 各分布に割り当てる色と線種を定義
manual_colors <- c(
`ロジスティック (μ=0, s=1)` = "blue",
`ロジスティック (μ=5, s=1)` = "red",
`ロジスティック (μ=0, s=2)` = "darkgreen",
`正規分布 (μ=0, σ≈1.8)` = "black"
)
manual_linetypes <- c(
`ロジスティック (μ=0, s=1)` = "solid",
`ロジスティック (μ=5, s=1)` = "solid",
`ロジスティック (μ=0, s=2)` = "solid",
`正規分布 (μ=0, σ≈1.8)` = "dashed"
)
# 5. ggplotを使用してチャートを描画
p <- ggplot(df_long, aes(x = x, y = density, color = distribution, linetype = distribution)) +
geom_line(linewidth = 1.1) +
scale_color_manual(values = manual_colors) +
scale_linetype_manual(values = manual_linetypes) +
labs(
title = "ロジスティック分布と正規分布の比較",
subtitle = "形状は似ているが、ロジスティック分布の方がわずかに裾が重い",
x = "xの値",
y = "確率密度",
color = "分布の種類",
linetype = "分布の種類"
) +
theme_minimal(base_size = 14) +
theme(
legend.position = "top",
plot.title = element_text(face = "bold"),
plot.subtitle = element_text(color = "gray40")
) +
guides(color = guide_legend(nrow = 2))
# チャートの表示
print(p)Figure 1 の解説
上記のRコードを実行すると、3つのロジスティック分布と1つの正規分布が描画されたチャート Figure 1 が生成されます。
-
ロジスティック (μ=0, s=1)(青線): 基準となる標準ロジスティック分布です。 -
ロジスティック (μ=5, s=1)(赤線): 位置パラメータ \(\mu\) を5にしたことで、青線の分布がそのまま右に5だけ平行移動しています。 -
ロジスティック (μ=0, s=2)(緑線): 尺度パラメータ \(s\) を2倍にしたことで、青線と比べて分布が広く、平たくなっています。 -
正規分布 (μ=0, σ≈1.8)(黒破線): 青線のロジスティック分布と同じ平均(0)と分散(\(\pi^2/3\))を持つ正規分布です。両者を比較すると、その形状が似ていることを確認できます。- 但し、ロジスティック分布(青線)の方が中心(\(x=0\))のピークが高く、裾の部分では正規分布よりもわずかに確率密度が高くなっています。この「わずかに重い裾」が、ロジスティック分布の性質を特徴づけています。
以上です。