Rで確率分布:一般化パレート分布

確率密度関数 (Probability Density Function, PDF)

GPDに従う確率変数 \(X\) の確率密度関数 \(f(x)\) は、3つのパラメータを用いて以下のように定義されます。

\[f\left(x | \xi, \sigma, \mu\right) = \dfrac{1}{\sigma} \left(1 + \xi \dfrac{x-\mu}{\sigma}\right)^{-(1/\xi + 1)}\]

この式は、形状パラメータ \(\xi \neq 0\) の場合に適用されます。\(\xi = 0\) の場合は、この式の極限として指数分布が現れます。

\[f\left(x | \xi=0, \sigma, \mu\right) = \dfrac{1}{\sigma} \exp\left(-\dfrac{x-\mu}{\sigma}\right)\]

この分布は、3つのパラメータによってその形状が決定されます。

• \(\mu\): 位置パラメータ (location parameter)
  • 分布の開始点となる閾値です。\(x \ge \mu\) の範囲で定義されます。
• \(\sigma\): 尺度パラメータ (scale parameter)
  • 分布の広がり（ばらつき）を決定する正のパラメータです。
• \(\xi\): 形状パラメータ (shape parameter)
  • 分布の裾の挙動を決定するパラメータです。この値の符号によって、分布の性質が根本的に変わります。
    • \(\xi > 0\): パレート型（ヘビーテール）。裾はべき乗的にゆっくりと減少し、分布が取りうる値（確率変数 \(x\) の値）に上限はありません。通常のパレート分布やコーシー分布などがこのファミリーに属します。
    • \(\xi = 0\): 指数型（ライトテール）。裾は指数的に速く減少します。このとき、GPDは指数分布と一致します。正規分布やガンマ分布などもこのファミリーに分類されます。
    • \(\xi < 0\): ベータ型（ショートテール）。分布は有限の点で終わり、上限が存在します（上限は \(\mu - \sigma/\xi\)）。一様分布やベータ分布などがこのファミリーです。

主な特徴

• 定義域: \(x \ge \mu\)。また、\(\xi < 0\) の場合は、さらに \(x \le \mu - \sigma/\xi\) という上限があります。
• 形状の柔軟性: 形状パラメータ \(\xi\) の値だけで、裾が非常に重い分布から、指数的な分布、さらには有限の裾を持つ分布まで、3つの全く異なるタイプの分布を統一的に表現できます。

Rコード

# 必要なライブラリを読み込みます
library(evd)
library(ggplot2)
library(dplyr)
library(tidyr)

# 1. 描画範囲となるx軸の値を生成
# ξ=-0.5 の場合、上限は μ - σ/ξ = 0 - 1/(-0.5) = 2 となる
x_vals <- seq(0, 8, length.out = 1000)

# 2. 異なるパラメータを持つGPDの確率密度を計算
# dgpd(x, loc, scale, shape) を使用
df <- tibble(
  x = x_vals
) %>%
  mutate(
    `ξ=0.5 (パレート型)` = dgpd(x, loc = 0, scale = 1, shape = 0.5),
    `ξ=0 (指数型)` = dgpd(x, loc = 0, scale = 1, shape = 0),
    `ξ=-0.5 (ベータ型)` = dgpd(x, loc = 0, scale = 1, shape = -0.5)
  )

# 3. ggplotで描画しやすいように、データを「ロングフォーマット」に変換
df_long <- df %>%
  pivot_longer(
    cols = -x,
    names_to = "parameters",
    values_to = "density"
  ) %>%
  # 凡例の順序を調整
  mutate(parameters = factor(parameters, levels = c(
    "ξ=0.5 (パレート型)",
    "ξ=0 (指数型)",
    "ξ=-0.5 (ベータ型)"
  )))

# 4. 各分布に割り当てる色を定義
manual_colors <- c(
  `ξ=0.5 (パレート型)` = "blue",
  `ξ=0 (指数型)` = "red",
  `ξ=-0.5 (ベータ型)` = "darkgreen"
)

# 5. ggplotを使用してチャートを描画
p <- ggplot(df_long, aes(x = x, y = density, color = parameters)) +
  # 密度がNAになる部分（定義域外）はプロットしない
  geom_line(data = . %>% filter(!is.na(density)), linewidth = 1.2) +
  scale_color_manual(values = manual_colors) +
  labs(
    title = "形状パラメータ(ξ)による一般化パレート分布(GPD)の変化",
    subtitle = "ξの符号によって、裾の挙動が3つのタイプに分かれる",
    x = "閾値からの超過量 (x)",
    y = "確率密度",
    color = "形状パラメータ (ξ)"
  ) +
  coord_cartesian(xlim = c(0, 8), ylim = c(0, 1.1)) +
  theme_minimal(base_size = 14) +
  theme(
    legend.position = "top",
    plot.title = element_text(face = "bold"),
    plot.subtitle = element_text(color = "gray40")
  )

# チャートの表示
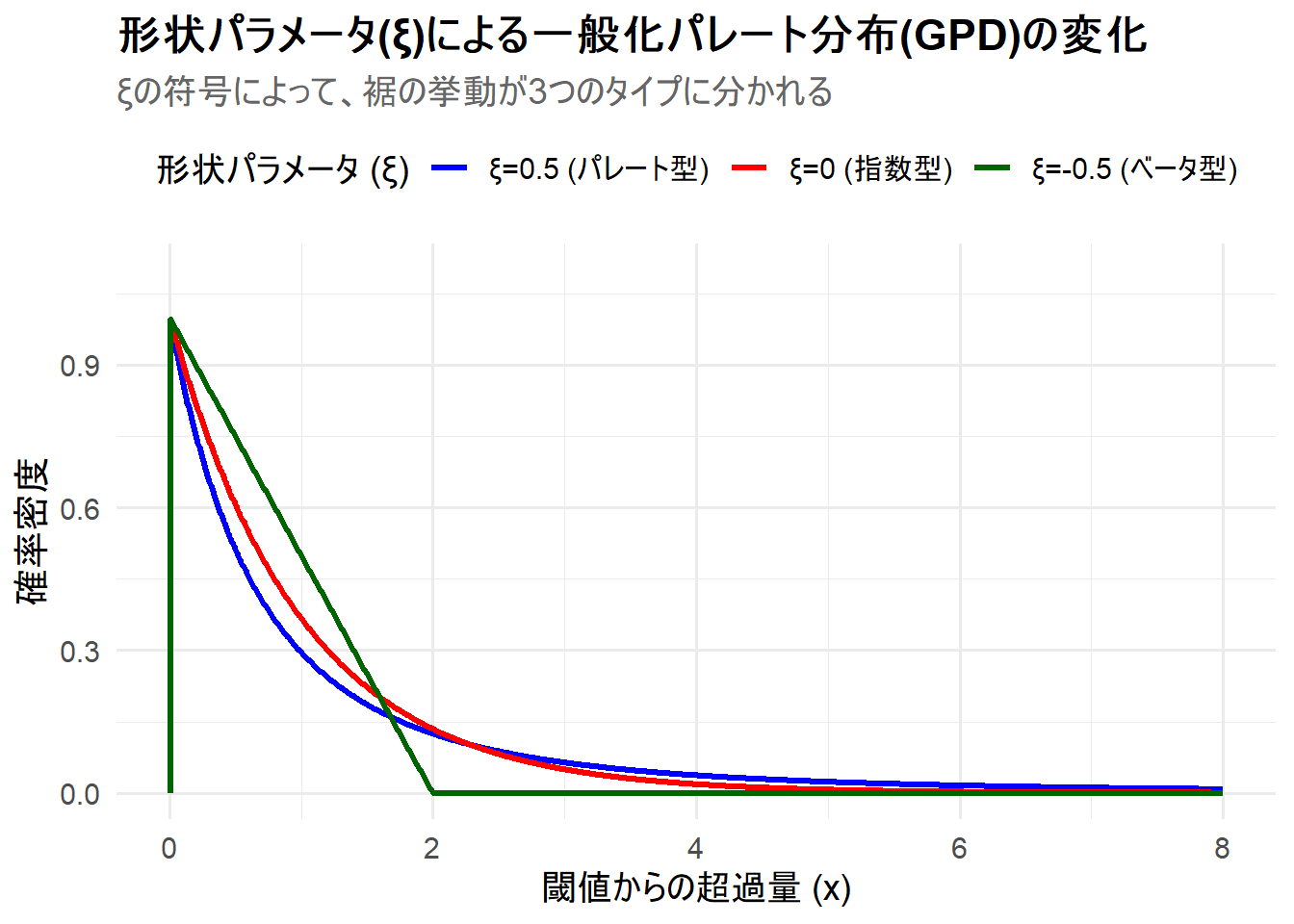
print(p)

Figure 1 の解説

上記のRコードを実行すると、3つのタイプのGPDが描画されたチャート Figure 1 が生成されます。

• ξ=0.5 (青線): パレート型。右側に非常に長く、重い裾を引いています。これは、極端に大きな値が発生する可能性が無視できないことを示しており、金融市場の暴落などのモデル化に利用されます。
• ξ=0 (赤線): 指数型。これは尺度パラメータが1の指数分布そのものです。裾は指数的に速く減少します。
• ξ=-0.5 (緑線): ベータ型。分布は \(x=2\) で途切れ、確率密度が0になっています。これは、この分布に従う現象には明確な物理的・理論的な上限が存在することを意味します。

このシミュレーションから、GPDが形状パラメータ \(\xi\) というたった一つのパラメータを調整するだけで、裾が無限に重い分布から、指数的な分布、そして有限の裾を持つ分布まで、質的に全く異なる3つのクラスの分布をシームレスに表現できる分布であることがわかります。

以上です。