Rで確率分布:二項分布

Rで 確率分布:二項分布 を試みます。

本ポストはこちらの続きです。

const typesetMath = (el) => { if (window.MathJax) { // MathJax Typeset window.MathJax.typeset(); } else if (window.katex...

1. 二項分布とは

二項分布（Binomial Distribution）は、離散確率分布の一つです。これは、「成功か失敗か」、「表か裏か」といった、結果が2種類しかない試行（ベルヌーイ試行）を、独立にn回繰り返したときに、成功する回数が従う分布です。

例えば、「コインを10回投げて、表が出る回数」や「100個の製品を検査して、不良品が見つかる個数」などが、二項分布に従う典型的な例です。

確率質量関数 (Probability Mass Function, PMF)

試行回数 \(n\)、成功確率 \(p\) の二項分布に従う確率変数 \(X\) が、特定の値 \(k\)（成功回数）をとる確率 \(P(X=k)\) は、以下の式で定義されます。

\[P\left(X=k | n, p\right) = \binom{n}{k} p^k \left(1-p\right)^{n-k} \quad (k=0, 1, 2, \dots, n)\]

この式は、以下の3つの要素から成り立っています。

\(\binom{n}{k} = \dfrac{n!}{k!(n-k)!}\): 組み合わせの数。\(n\)回の試行の中から、成功する\(k\)回をどの順番で選ぶかのパターン数です。
\(p^k\): 成功がk回起こる確率。
\((1-p)^{n-k}\): 失敗がn-k回起こる確率。

この分布は、2つのパラメータによってその形状が決定されます。

\(n\): 試行回数 (number of trials)
- 独立なベルヌーイ試行を繰り返す回数です。正の整数です。
\(p\): 成功確率 (probability of success)
- 1回の試行で「成功」と見なす結果が起こる確率です。\(0 \le p \le 1\) の範囲の値をとります。

主な特徴

定義域: 成功回数 \(k\) がとりうる値は、0から試行回数nまでの整数です。
形状:
- \(p=0.5\) のとき、分布は左右対称な釣鐘型になります。
- \(p < 0.5\) のとき、分布は右に歪んだ形状になります。
- \(p > 0.5\) のとき、分布は左に歪んだ形状になります。
- 試行回数 \(n\) が大きくなるにつれて、分布の形状は（\(p\)が0や1に極端に近くない限り）正規分布で近似できるようになります（ド・モアブル–ラプラスの定理）。
代表値:
- 平均 (Mean): \(E[X] = np\)
- 分散 (Variance): \(V[X] = np(1-p)\)
他の分布との関係:
- ベルヌーイ分布: 試行回数 \(n=1\) の二項分布は、ベルヌーイ分布と一致します。
- ポアソン分布: \(n\) が非常に大きく、\(p\) が非常に小さい場合、\(\lambda = np\) のポアソン分布で近似できます。

2. 二項分布の応用例

結果が2値で表される試行の繰り返しは、現実世界に数多く存在します。

品質管理
- 工場で生産された製品を \(n\) 個抜き取って検査したときの、不良品の個数。
A/Bテスト・マーケティング
- \(n\) 人のユーザーに新しいWebサイトのデザインを見せたときの、コンバージョン（購入や登録）した人数。
- \(n\) 人にダイレクトメールを送ったときの、返信があった人数。
医療・薬学
- \(n\) 人の患者に新薬を投与したときの、副作用が出た（あるいは、効果があった）患者の数。
世論調査
- \(n\) 人の有権者に質問したときの、ある政策への賛成者の数。
遺伝学
- ある遺伝子を持つ両親から生まれる \(n\) 人の子供のうち、特定の遺伝形質を受け継ぐ子供の数。

3. R言語によるシミュレーション

ここでは、試行回数 \(n\) と成功確率 \(p\) を変更した4つの二項分布を1枚のチャートに描画します。ポアソン分布と同様にロリポップチャートで表現します。

ケース1: n=20, p=0.5 （対称な釣鐘型）
ケース2: n=20, p=0.2 （右に歪んだ形状）
ケース3: n=20, p=0.8 （左に歪んだ形状）
ケース4: n=100, p=0.5 （試行回数が大きく、正規分布に近い形状）

Rコード

# 必要なライブラリを読み込みます
library(ggplot2)
library(dplyr)
library(tidyr)

# 1. 異なるパラメータを持つ二項分布の確率質量を計算
# dbinom(k, size, prob) を使用。sizeがn, probがp
df <- tibble(
  k = 0:100
) %>%
  mutate(
    `n=20, p=0.5`  = dbinom(k, size = 20, prob = 0.5),
    `n=20, p=0.2`  = dbinom(k, size = 20, prob = 0.2),
    `n=20, p=0.8`  = dbinom(k, size = 20, prob = 0.8),
    `n=100, p=0.5` = dbinom(k, size = 100, prob = 0.5)
  )

# 2. ggplotで描画しやすいように、データを「ロングフォーマット」に変換
df_long <- df %>%
  pivot_longer(
    cols = -k,
    names_to = "parameters",
    values_to = "probability"
  ) %>%
  # 確率が非常に小さいものは除外してプロットを見やすくする
  filter(probability > 1e-6) %>%
  # 凡例の順序を調整
  mutate(parameters = factor(parameters, levels = c(
    "n=20, p=0.5",
    "n=20, p=0.2",
    "n=20, p=0.8",
    "n=100, p=0.5"
  )))

# 3. 各分布に割り当てる色を定義
manual_colors <- c(
  `n=20, p=0.5`  = "blue",
  `n=20, p=0.2`  = "red",
  `n=20, p=0.8`  = "darkgreen",
  `n=100, p=0.5` = "purple"
)

# 4. ggplotを使用してチャートを描画（ファセットで分割）
p <- ggplot(df_long, aes(x = k, y = probability, color = parameters)) +
  geom_segment(aes(xend = k, yend = 0), linewidth = 0.8) +
  geom_point(size = 2.5) +
  facet_wrap(~parameters, ncol = 2, scales = "free") +
  scale_color_manual(values = manual_colors) +
  labs(
    title = "パラメータ(n, p)による二項分布の変化",
    subtitle = "p=0.5で対称、nが大きいと正規分布に近づく",
    x = "成功回数 (k)",
    y = "確率"
  ) +
  theme_minimal(base_size = 14) +
  theme(
    legend.position = "none",
    plot.title = element_text(face = "bold"),
    plot.subtitle = element_text(color = "gray40"),
    strip.text = element_text(face = "bold", size = 12)
  )

# チャートの表示
print(p)

Figure 1 の解説

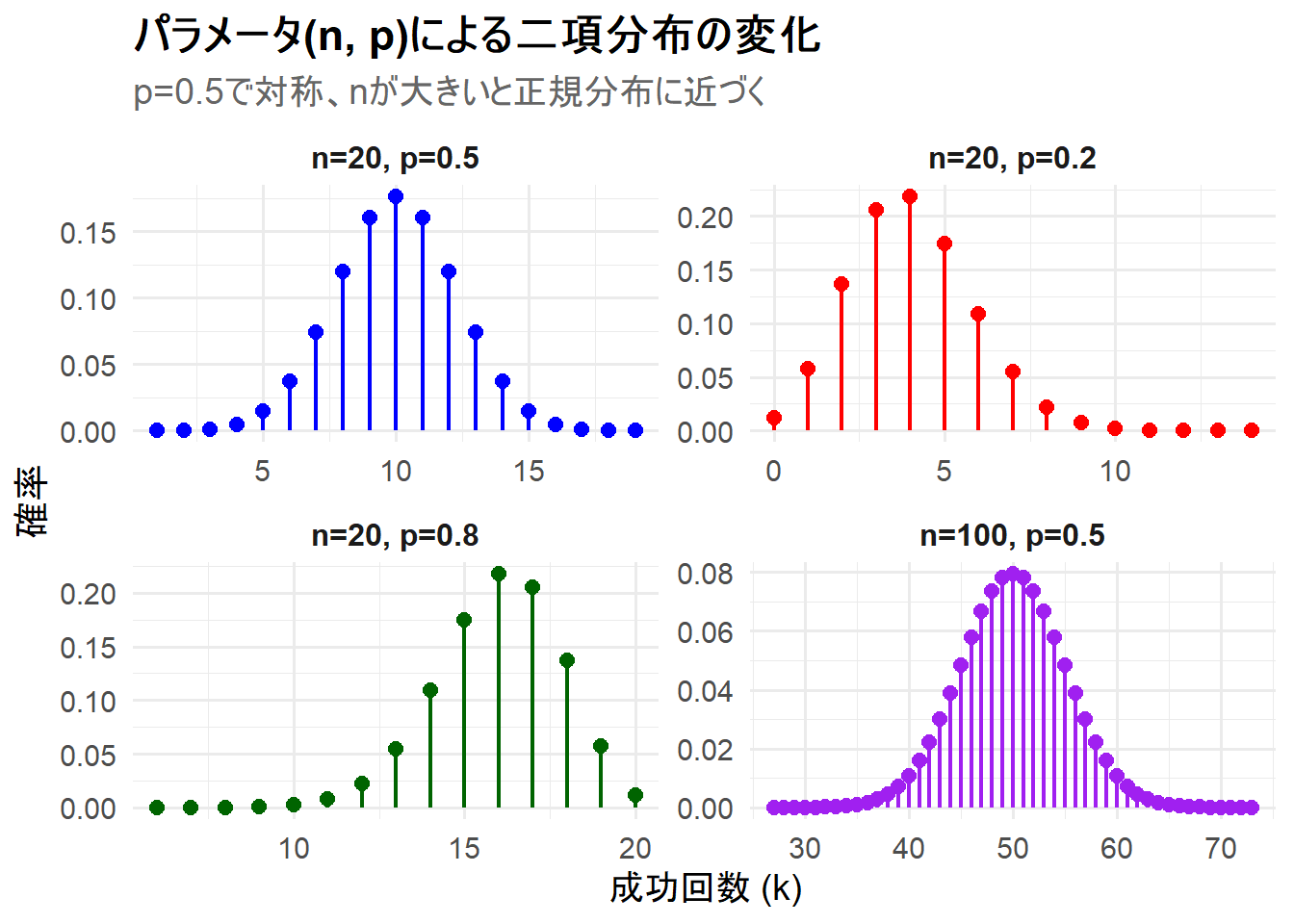
上記のRコードを実行すると、4つの二項分布が描画されたチャート Figure 1 が生成されます。

n=20, p=0.5 (左上): 成功確率が0.5なので、分布は平均 \(np=10\) を中心とした左右対称な釣鐘型になっています。
n=20, p=0.2 (右上): 成功確率が0.5より小さいため、分布は左に寄っており（平均は \(np=4\)）、右に歪んだ形状をしています。成功回数が少ない方に確率が偏っています。
n=20, p=0.8 (左下): 成功確率が0.5より大きいため、分布は右に寄っており（平均は \(np=16\)）、左に歪んだ形状をしています。成功回数が多い方に確率が偏っています。
n=100, p=0.5 (右下): 試行回数 \(n\) が100と大きくなっています。\(p=0.5\) のため対称なのはもちろんですが、個々の点の離散的な性質が目立たなくなり、全体として滑らかな、正規分布に似た釣鐘型になっていることがわかります。

以上です。