Rで統計的因果推論:傾向スコア・マッチング

目的

統計的因果推論の目的は、ある「処置（介入）」が「結果（アウトカム）」に与える因果効果を明らかにすることです。例えば、「新しい薬を飲む（処置）」と「病気が治る（結果）」の関係などです。

信頼性の高い一つの推論方法は、ランダム化比較試験（RCT）です。対象者をランダムに処置群と対照群に分けることで、両群の背景（年齢、性別、重症度など）が統計的に均質になり、結果の差を純粋な処置の効果として評価できます。

しかし、倫理的・コスト的な問題でRCTが実施できない場合も多く、私たちは手元にある観察データ（例：診療記録、アンケート調査）から因果効果を推定しなくてはなりません。観察データでは、処置を受けるかどうかが個人の意思や状況によって決まるため、処置群と対照群の背景に偏りが生じます。これをセレクションバイアスと呼びます。

例えば、「健康意識が高い人ほど新しいサプリを摂取しやすく、かつ健康意識が高いこと自体が健康につながる」という場合、「健康意識」が処置（サプリ摂取）と結果（健康）の両方に影響を与え、サプリの真の効果を見誤らせます。このような変数を交絡因子と呼びます。

傾向スコア・マッチングは、このような観察データにおけるセレクションバイアス（特に交絡バイアス）を調整し、あたかもランダム化比較試験を行ったかのような状況を作り出すことで、より妥当な因果効果を推定するための手法の一つです。

傾向スコアの定義

傾向スコア（Propensity Score）は、個々の対象者の背景的な特徴（共変量）が与えられたときに、その対象者が処置群に割り当てられる条件付き確率として定義されます。数式で表すと以下のようになります。

\[
e\left(X_i\right) = P\left(Z_i=1 | X_i\right)
\]

ここで、

• \(e\left(X_i\right)\) は対象者 \(i\) の傾向スコア
• \(Z_i\) は対象者 \(i\) が処置を受けたかどうかを示す変数（受けた場合 \(Z_i=1\), 受けなかった場合 \(Z_i=0\)）
• \(X_i\) は対象者 \(i\) の共変量（年齢、性別、病気の重症度など）のベクトル

です。

この傾向スコアには、「共変量 \(X_i\) が同じであれば、処置の割り当て \(Z_i\) と潜在的なアウトカムは独立である」という重要な性質があります。つまり、傾向スコアが同じ値を持つ人々を集めれば、その集団内では処置がランダムに割り当てられたのと同じ状況と見なせます。

マッチングの手順

傾向スコア・マッチングは、主に以下のステップで実行されます。

1. 傾向スコアの推定: 共変量 \(X\) を説明変数、処置の有無 \(Z\) を目的変数として、ロジスティック回帰モデルなどを用いて各個人の傾向スコア \(e\left(X_i\right)\) を推定します。

2. マッチング: 推定した傾向スコアが近い値を持つ個人を、処置群 (\(Z=1\)) と対照群 (\(Z=0\)) から探し出し、ペアを作ります。最も単純な方法は、処置群の各個人に対して、最も傾向スコアが近い対照群の個人を1人見つける「最近傍マッチング」です。

3. バランスの確認: マッチング後に作成された新しいデータセットで、処置群と対照群の共変量の分布（平均値など）が均質になっているか（バランスが取れているか）を確認します。バランスが取れていなければ、モデルの修正やマッチング方法の変更を検討します。

4. 効果の推定: 共変量のバランスが取れたことを確認した後、マッチング後のデータセットを使って処置群と対照群のアウトカムの平均差を計算します。この差が、交絡バイアスを調整した後の処置の因果効果（Average Treatment effect on the Treated, ATT）の推定値となります。

準備

まず、シミュレーションに必要なパッケージを読み込みます。MatchItは傾向スコア・マッチングを実行するため、cobaltはLove Plot作成のために使用します。

# パッケージの読み込み
library(tidyverse)
library(MatchIt)
library(cobalt)

# 結果の再現性を担保するための乱数シード固定
seed <- 20250824

Step 1: データ生成

シナリオに沿ったシミュレーションデータを作成します。生徒1000人分のデータを作ります。

• motivation（学習意欲）と income（家庭の経済状況）を生成します。
• これら2つの交絡因子が高いほど、プログラムに参加 (participation = 1) しやすくなるように設定します。
• テストの点数 score は、「学習意欲」、「家庭の経済状況」そして「プログラム参加」のすべてに影響を受けるように設定します。
• ここで、プログラム参加の真の効果（tau）を10点と設定します。私たちの最終目標は、この10点という値をデータから正しく推定することです。

set.seed(seed)

# サンプルサイズ
n <- 1000

# 交絡因子（共変量）の生成
# X1: 学習意欲（標準正規分布に従う）
motivation <- rnorm(n, mean = 5, sd = 1)
# X2: 家庭の経済状況（標準正規分布に従う）
income <- rnorm(n, mean = 5, sd = 1.5)

# 処置（プログラム参加）の割り当て
# 学習意欲と経済状況が高いほど、参加確率が高くなるロジットモデル
# plogisはロジスティックシグモイド関数
participation_prob <- plogis(-4 + 0.5 * motivation + 0.5 * income)
participation <- rbinom(n, 1, participation_prob)

# 結果（テストの点数）の生成
# 真の因果効果 (tau) を 10点 とする
tau <- 10
# 誤差項
epsilon <- rnorm(n, 0, 10)
# テストの点数は、基礎点 + 介入効果 + 交絡因子の効果 + 誤差
score <- 50 + tau * participation + 5 * motivation + 4 * income + epsilon

# データフレームの作成
sim_data <- tibble(
  id = 1:n,
  motivation = motivation,
  income = income,
  participation = factor(participation, levels = c(0, 1), labels = c("不参加", "参加")),
  score = score
)

cat("--- 生成したデータの一部を確認 ---\n")
head(sim_data)

--- 生成したデータの一部を確認 ---
# A tibble: 6 × 5
     id motivation income participation score
  <int>      <dbl>  <dbl> <fct>         <dbl>
1     1       4.02   4.26 参加          103. 
2     2       6.33   5.06 参加          123. 
3     3       4.59   3.74 参加           97.0
4     4       3.76   4.36 参加           96.9
5     5       5.52   6.99 参加          102. 
6     6       4.77   2.80 参加          108. 

Step 2: マッチング前の分析（バイアスを含んだ単純比較）

まず、傾向スコア・マッチングを行わずに、単純に参加者と不参加者のテストの点数を比較してみます。

cat("--- マッチング前の単純比較 ---\n")

# t検定による平均点の比較
t_test_before <- t.test(score ~ participation, data = sim_data)
print(t_test_before)

# 結果の表示
mean_scores_before <- sim_data |>
  group_by(participation) |>
  summarise(mean_score = mean(score))

cat(sprintf(
  "\n不参加者の平均点: %.2f\n参加者の平均点: %.2f\n",
  mean_scores_before$mean_score[1], mean_scores_before$mean_score[2]
))
cat(sprintf(
  "単純な平均点の差 (見かけの効果): %.2f\n",
  diff(mean_scores_before$mean_score)
))

--- マッチング前の単純比較 ---

    Welch Two Sample t-test

data:  score by participation
t = -18.717, df = 619.27, p-value < 2.2e-16
alternative hypothesis: true difference in means between group 不参加 and group 参加 is not equal to 0
95 percent confidence interval:
 -17.92737 -14.52263
sample estimates:
mean in group 不参加   mean in group 参加 
            90.35892            106.58392 


不参加者の平均点: 90.36
参加者の平均点: 106.58
単純な平均点の差 (見かけの効果): 16.22

単純に平均点を比較すると、その差は約 16.22点 となりました。これは私たちが設定した真の効果（10点）よりも大きな値です。これが「プラグラム参加者は不参加者よりも「学習意欲」と「家庭の経済状況」が平均的に高い集団に設定」した交絡バイアスの影響です。

その元々の差が、テストの点数を押し上げ、プログラムの効果を過大評価させているのです。

Step 3: 傾向スコア・マッチングの実施

それでは、MatchItパッケージを使って傾向スコア・マッチングを実行し、交絡因子のバランスを整えましょう。ここでは、処置群の各個人に対し、傾向スコアが最も近い対照群の個人を1人見つけてくる1:1の最近傍マッチングを行います。

# 傾向スコア・マッチングの実行
# participation ~ motivation + income という式で、
# motivationとincomeからparticipationを予測するモデル（傾向スコアモデル）を立てる
# replace = FALSE（復元なし）:
# 一度マッチング相手として選ばれた対照群の人は、他の処置群の人の相手として二度と選ばれない。
# replace = TRUE（復元あり）:
# 一人の対照群の人が、複数の処置群の人のマッチング相手として繰り返し選ばれる。
# 対照群（Control）と処置群（Treated）の人数の不均衡を考慮して、replace = TRUE とする。
match_result <- matchit(
  participation ~ motivation + income,
  data = sim_data,
  method = "nearest", # 最近傍マッチング
  distance = "logit", # ロジスティック回帰で傾向スコアを推定
  replace = TRUE # 復元抽出を許可
)

cat("--- マッチング結果の要約 ---\n")
summary(match_result, un = TRUE) # un=TREU でマッチング前の情報を表示

--- マッチング結果の要約 ---

Call:
matchit(formula = participation ~ motivation + income, data = sim_data, 
    method = "nearest", distance = "logit", replace = TRUE)

Summary of Balance for All Data:
           Means Treated Means Control Std. Mean Diff. Var. Ratio eCDF Mean eCDF Max
distance          0.7216        0.5943          0.8685     0.7079    0.2103   0.2995
motivation        5.1105        4.7018          0.4388     0.9142    0.1227   0.2235
income            5.2738        4.3738          0.6207     1.0695    0.1707   0.2572

Summary of Balance for Matched Data:
           Means Treated Means Control Std. Mean Diff. Var. Ratio eCDF Mean eCDF Max Std. Pair Dist.
distance          0.7216        0.7209          0.0049     1.0065    0.0030   0.0382          0.0124
motivation        5.1105        5.0567          0.0578     0.9453    0.0312   0.0808          0.9650
income            5.2738        5.3031         -0.0202     1.0931    0.0201   0.0631          0.6851

Sample Sizes:
              Control Treated
All            319.       681
Matched (ESS)   98.36     681
Matched        213.       681
Unmatched      106.         0
Discarded        0.         0

4. マッチング結果

指標	変数	マッチング前 (All)	マッチング後 (Matched)	評価
SMD	motivation	0.4388	0.0578	絶対値が0.1以下になり改善
SMD	income	0.6207	-0.0202	絶対値が0.1以下になり改善
分散比	motivation	0.9142	0.9453	どちらも理想値の1に近い
分散比	income	1.0695	1.0931	どちらも理想値の1に近い
eCDF Mean	motivation	0.1227	0.0312	理想値の0に近く改善
eCDF Mean	income	0.1707	0.0201	理想値の0に近く改善
eCDF Max	motivation	0.2235	0.0808	理想値の0に近く改善
eCDF Max	income	0.2572	0.0631	理想値の0に近く改善

• Summary of Balance for All Data: マッチング前の指標
• Summary of Balance for Matched Data: マッチング後の指標

このバランス改善を可視化します。

# バランスの可視化 (Love Plot)
love.plot(
  match_result,
  abs = FALSE, # 絶対値ではなく元の値でプロット
  stats = "mean.diffs", # 平均差をプロット
  thresholds = c(m = .1) # バランス改善の目安となる閾値(0.1)を線で示す
) +
  labs(title = "マッチング前後の共変量(平均差)のバランス") +
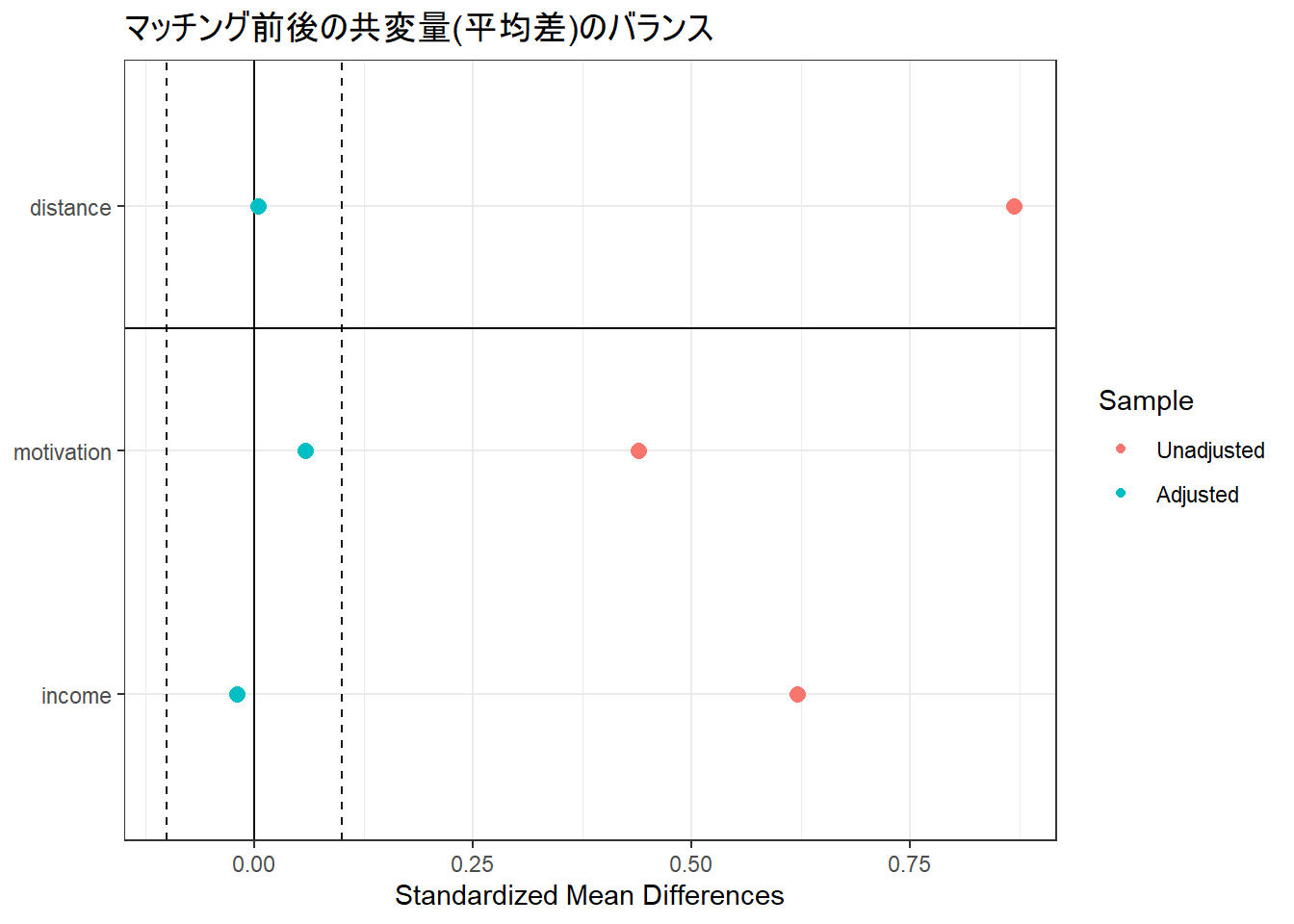
  theme_bw()

Figure 1 は「Love Plot（ラブプロット）」と呼ばれ、傾向スコア・マッチングの前後で、処置群（プログラム参加者）と対照群（不参加者）の背景的な特徴（共変量）のバランスがどれだけ改善したかを視覚的に確認するためのものです。

Figure 1 を見ることで、マッチングが交絡バイアスを適切に調整できたかどうかを評価することができます。

Figure 1 の各要素の見方

• 縦軸 (Y-axis): バランスを評価している変数です。
  • motivation: 学習意欲
  • income: 家庭の経済状況
  • distance: 傾向スコアそのもの
• 横軸 (X-axis): 「標準化平均差 (Standardized Mean Differences)」を表します。これは、処置群と対照群の平均値の差を、データのばらつき（標準偏差）で割った指標です。
  • 0.0 の位置（中央の黒い実線）は、両群の平均値が完全に一致しており、完璧にバランスが取れている状態を意味します。
  • この値が0から離れるほど、両群のバランスが悪いことを示します。
• 点の色:
  • 赤色の点 (Unadjusted): マッチングを行う前の、元のデータにおけるバランス状態を示します。
  • 青色の点 (Adjusted): マッチングを行った後の、新しいデータにおけるバランス状態を示します。
• 縦の破線: バランスが良好かどうかの目安を示す閾値です。一般的に、標準化平均差の絶対値が 0.1 以内（この破線の内側）に収まっていれば、バランスは十分に改善されたと判断されます。

Figure 1 から読み取れること

1. マッチング前の問題点（赤色の点）: マッチング前の赤色の点を見ると、motivationもincomeも0から大きく右側に離れていることがわかります。これは、元のデータでは、プログラム参加者の方が不参加者に比べて「学習意欲」も「家庭の経済状況」も平均的に高かった（= セレクションバイアスが存在した）ことを示唆しています。

2. マッチング後の改善効果（青色の点）: 一方、マッチング後の青色の点に注目すると、すべての変数が中央の 0.0 の線に近く、かつ目安である ±0.1 の破線の内側に収まっていることがわかります。

結論

マッチングによって、もともと存在した「学習意欲」と「家庭の経済状況」という交絡因子の偏りが取り除かれました。その結果、あたかもランダム化比較試験（RCT）を行ったかのように、処置群と対照群の背景が均質化されたデータセットが作成されました。

このバランスの取れたデータを用いて効果を推定することで、セレクションバイアスの影響を排した、より信頼性の高いプログラムの因果効果を明らかにすることができます。

Step 4: マッチング後の分析（効果推定）

共変量のバランスが取れたデータセットを使って、再度プログラムの効果を推定します。

cat("--- マッチング後の効果推定 ---\n")

# マッチング後のデータを取得
matched_data <- match.data(match_result)

# マッチング後のデータで効果を推定
# replace=TRUE の場合、対照群のウェイトを考慮した分析が必要
# たくさん選ばれた対照群の人は大きな重みを持ちます
# ここではlm()を使ってウェイト付き回帰分析を行います(加重最小二乗法)
model_after_match <- lm(score ~ participation, data = matched_data, weights = weights)
effect_estimate <- coef(model_after_match)["participation参加"]

# 結果の表示
cat(sprintf(
  "マッチング後の平均点の差 (調整後の効果): %.2f\n",
  effect_estimate
))

--- マッチング後の効果推定 ---
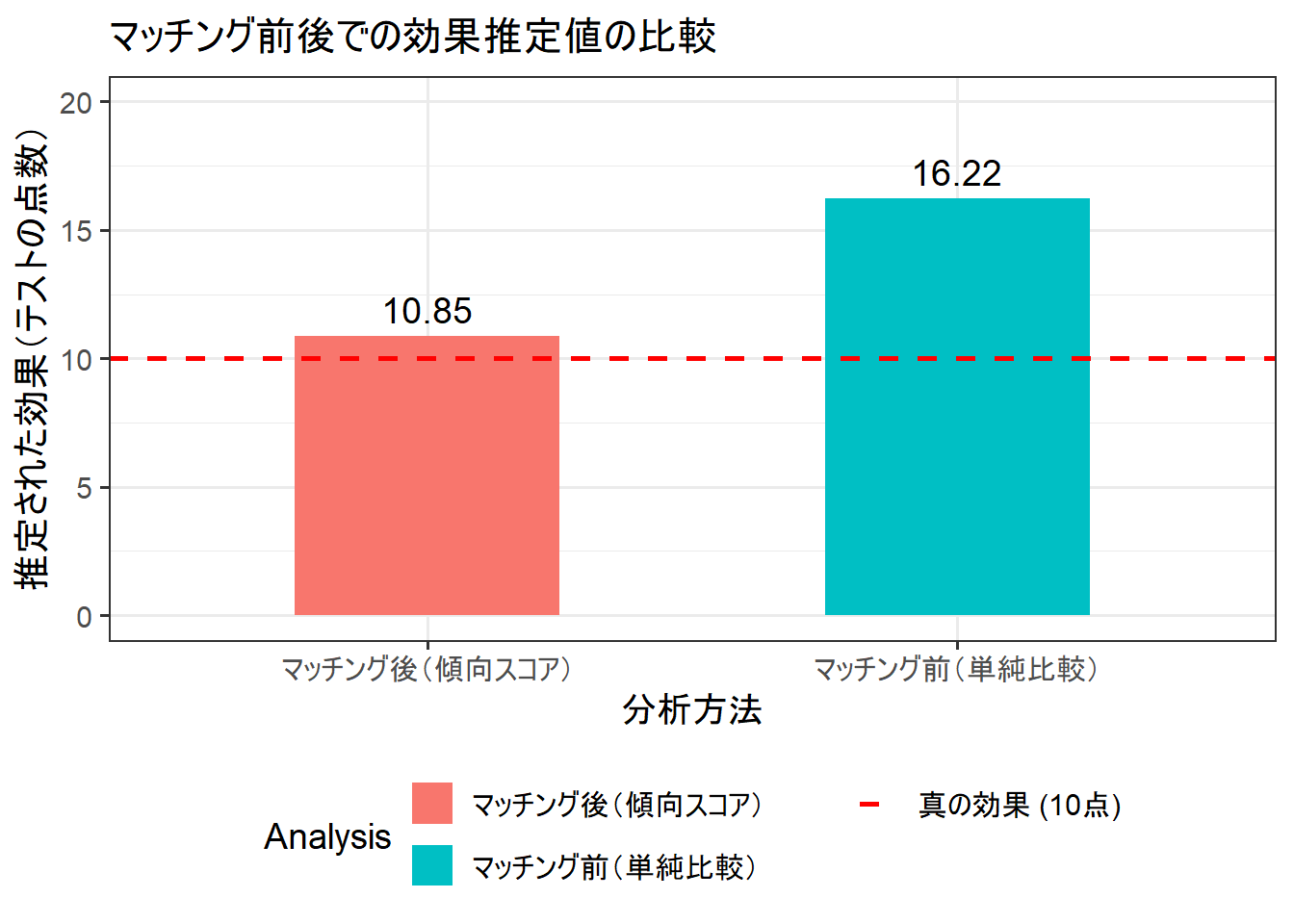
マッチング後の平均点の差 (調整後の効果): 10.85

マッチング後のデータで平均点を比較すると、その差は 10.85点 となりました。これは、私たちが最初に設定した真の効果（10点）に近い値です。

Step 5: 結果のまとめと考察

最後に、マッチング前後の結果を比較してみましょう。

# 結果をまとめたデータフレーム
results_summary <- tibble(
  Analysis = c("マッチング前（単純比較）", "マッチング後（傾向スコア）"),
  Estimated_Effect = c(
    diff(mean_scores_before$mean_score),
    effect_estimate
  ),
  True_Effect = tau
)

# 結果のプロット
ggplot(results_summary, aes(x = Analysis, y = Estimated_Effect, fill = Analysis)) +
  geom_col(width = 0.5) +
  geom_hline(aes(yintercept = True_Effect, linetype = "真の効果 (10点)"), color = "red", linewidth = 1) +
  geom_text(aes(label = sprintf("%.2f", Estimated_Effect)), vjust = -0.5, size = 5) +
  scale_y_continuous(limits = c(0, 20)) +
  scale_linetype_manual(name = "", values = "dashed") +
  labs(
    title = "マッチング前後での効果推定値の比較",
    x = "分析方法",
    y = "推定された効果（テストの点数）"
  ) +
  theme_bw(base_size = 14) +
  theme(legend.position = "bottom") +
  guides(fill = guide_legend(nrow = 2))

今回のシミュレーションから、以下のことがわかります。

• 単純比較の危険性: 交絡因子が存在する観察データで単純に処置群と対照群を比較すると、セレクションバイアスの影響で因果効果を大きく誤って推定してしまいます（16.22点 vs 真の効果10点）。
• 傾向スコア・マッチングの有効性: 傾向スコアを用いて背景の似た個人同士をマッチングさせることで、交絡因子の影響を調整し、より真実に近い因果効果を推定することができました（10.85点 vs 真の効果10点）。

このように、傾向スコア・マッチングは、RCTが実施できない観察研究において、交絡バイアスを低減し、より信頼性の高い因果効果を推定するための一つの方法です。

以上です。