Rで 統計的因果推論:自然実験-回帰不連続デザイン を試みます。
本ポストはこちらの続きです。

また、関数 rdrobust {rdrobust} については、こちらを参照してください。

1. 「回帰不連続デザイン(RDD)」とは
回帰不連続デザイン(Regression Discontinuity Design, RDD)は、ある介入(処置)が、連続的な指標(割り当て変数)に基づいて、特定の閾値(カットオフ)を超えたかどうかで割り当てられる状況を利用して因果効果を推定する手法です。
RDDの根幹にあるアイデアは、「カットオフのすぐ近くでは、介入を受けるか受けないかは、ほとんどランダムに決まっている」というものです。
例えば、試験の点数が60点以上で合格(介入)、59点以下で不合格だとします。このとき、59.9点を取った人と60点を取った人の能力や意欲には本質的な差はないと考えられます。彼らの運命を分けたのは、偶然の範囲内のわずかな差だけです。この「カットオフをまたぐ偶然性」を擬似的なランダム化とみなし、カットオフの前後で結果(アウトカム)に不連続なジャンプが見られれば、それを介入による因果効果と解釈します。
RDDにはいくつかの種類があります。
- シャープRDD (Sharp RDD) vs ファジーRDD (Fuzzy RDD)
- シャープRDD: カットオフによって介入の有無が完全に(100%)決まる場合。今回のシミュレーションはこちらを扱います。
- ファジーRDD: カットオフによって介入を受ける確率が不連続に変化するが、100%ではない場合。
- パラメトリックRDD vs ノンパラメトリックRDD
- パラメトリックRDD: 割り当て変数と結果の関係を、特定の関数形(例:線形、二次関数)で仮定して分析します。
- ノンパラメトリックRDD: 関数形を仮定せず、カットオフ近傍のデータのみを用いて局所的に回帰分析を行います。
ノンパラメトリックRDDでは、カットオフを挟んだごく狭い範囲(バンド幅)のデータに注目し、その範囲内で局所線形回帰などを行います。そして、カットオフ地点での回帰線の予測値の差を因果効果として推定します。この効果は局所的平均処置効果(Local Average Treatment Effect, LATE)と呼ばれ、カットオフ近傍のデータセットに対する効果を測るものとなります。
2. シミュレーションのシナリオ:「特進クラスは学力を向上させるか?」
ある高校が、生徒の学力向上施策の一環として、入学試験の成績に基づいて「特進クラス」を編成することにしました。
【状況設定】
- 割り当て変数: 入学試験の点数(0点〜100点の連続値)。
- カットオフ: 80点。
- 介入(処置): 「特進クラス」への参加。
- 割り当てルール(シャープRDD):
- 入学試験の点数が80点以上だった生徒は、全員が特進クラスに振り分けられる。
- 入学試験の点数が80点未満だった生徒は、誰も特進クラスに入れない。
- 結果(アウトカム): 1年後に実施された全国模試の偏差値。
【研究の問い】
- 特進クラスへの参加は、生徒の1年後の模試の偏差値を向上させる効果があるのでしょうか?
【分析デザイン:回帰不連続デザイン(RDD)】
単純に特進クラス(介入群)と通常クラス(対照群)の模試の偏差値を比較するだけでは、元々入学試験の成績が良い生徒が特進クラスに入っているため、その効果を正しく測れません(セレクションバイアス)。
そこでRDDを用います。入学試験の点数がカットオフである80点のごく近く、例えば79.9点の生徒と80点の生徒を比較します。この2人の生徒の元々の学力はほぼ同じはずです(と、設定します)。もし、この2人の1年後の模試の偏差値に系統的な差(ジャンプ)があれば、それは特進クラスという介入によってもたらされた因果効果だと考えられます。
介入効果\(\tau\)は以下のように、カットオフ\(c\)における結果\(Y\)の期待値の左右からの極限の差として定義されます。
\[
\tau_{RDD} = \lim_{x \to c^{+}} E\left[Y_i | X_i = x\right] - \lim_{x \to c^{-}} E\left[Y_i | X_i = x\right]
\]
ここで、\(Y_i\)は生徒\(i\)の結果(模試の偏差値)、\(X_i\)は割り当て変数(入学試験の点数)です。
それでは、このシナリオをRでシミュレーションしてみましょう。
3. Rによるシミュレーション
3.1. シミュレーションの準備とデータ生成
まず、必要なパッケージを読み込み、シナリオに沿ったシミュレーションデータを作成します。
- 2000人の生徒のデータを生成します。
- 入学試験の点数と1年後の模試の偏差値の間には、自然な正の相関があるとします(入学試験の点数が1点高いと、模試の偏差値は平均的に0.5高くなる)。
- 特進クラスの真の因果効果として、特進クラスに参加した生徒は、この自然な学力の伸びに加えて、偏差値が平均で5ポイント上乗せされると設定します。
- 個人の能力や学習状況のばらつきを表す誤差も加えます。
# 必要なパッケージを読み込み
library(tidyverse)
library(rdrobust) # RDD分析用パッケージ
library(knitr)
# 結果を再現可能にするための乱数シード設定
seed <- 20250827
set.seed(seed)
# シミュレーションのパラメータ設定
n <- 2000 # 生徒の数
cutoff <- 80 # 特進クラスのカットオフ点
treatment_effect <- 5 # 特進クラスの真の因果効果(偏差値の上昇分)
# データ生成
sim_data_rdd <- tibble(
# 割り当て変数:入学試験の点数 (50点から100点の間に一様に分布)
score_entrance = runif(n, min = 50, max = 100)
) |>
# 介入変数と結果変数を生成
mutate(
# 介入ダミー (カットオフ以上なら1, 未満なら0)
treatment = if_else(score_entrance >= cutoff, 1, 0),
# 結果変数:1年後の模試の偏差値
# (入学試験の点数と自然な関係があり、介入効果が上乗せされる)
score_mock = 30 + # ベースラインの偏差値
0.5 * score_entrance + # 入学試験の点数との自然な関係
treatment_effect * treatment + # ★特進クラスの因果効果★
rnorm(n, mean = 0, sd = 4), # 個人のばらつき
.keep = "all"
) |>
# プロット用にクラス名を付与
mutate(
class_type = if_else(treatment == 1, "特進クラス(介入群)", "通常クラス(対照群)")
)
# 生成したデータのプレビュー
cat("##### 生成されたデータのプレビュー #####\n")
kable(head(sim_data_rdd))##### 生成されたデータのプレビュー #####| score_entrance | treatment | score_mock | class_type |
|---|---|---|---|
| 57.54451 | 0 | 65.40501 | 通常クラス(対照群) |
| 61.78445 | 0 | 62.46856 | 通常クラス(対照群) |
| 65.61502 | 0 | 67.86970 | 通常クラス(対照群) |
| 62.00193 | 0 | 64.03200 | 通常クラス(対照群) |
| 88.02648 | 1 | 73.45328 | 特進クラス(介入群) |
| 92.36702 | 1 | 80.91982 | 特進クラス(介入群) |
上記コード中のtreatment_effect * treatmentの項が、入学試験の点数が80点以上の生徒にのみ加算される「特進クラスの効果」を表しています。
3.2. rdrobustによるノンパラメトリックRDD分析
次に、rdrobustパッケージのrdrobust()関数を用いて、ノンパラメトリックRDD分析を実行します。この関数は、最適なバンド幅を自動で計算し、頑健な因果効果を推定してくれます。
# RDD分析の実行
rdd_result <- rdrobust(
y = sim_data_rdd$score_mock, # 結果変数
x = sim_data_rdd$score_entrance, # 割り当て変数
c = cutoff # カットオフ値
)
# 結果のサマリーを表示
cat("##### rdrobustによる分析結果 #####\n")
summary(rdd_result)##### rdrobustによる分析結果 #####
Sharp RD estimates using local polynomial regression.
Number of Obs. 2000
BW type mserd
Kernel Triangular
VCE method NN
Number of Obs. 1180 820
Eff. Number of Obs. 304 327
Order est. (p) 1 1
Order bias (q) 2 2
BW est. (h) 7.362 7.362
BW bias (b) 12.065 12.065
rho (h/b) 0.610 0.610
Unique Obs. 1180 820
=====================================================================
Point Robust Inference
Estimate z P>|z| [ 95% C.I. ]
---------------------------------------------------------------------
RD Effect 4.990 6.702 0.000 [3.433 , 6.270]
=====================================================================【結果の読み方】
summary()関数の出力は、分析の設定(使用されたデータ数、バンド幅の計算方法など)と、主要な推定結果の2つの部分から構成されています。因果効果の大きさやその統計的有意性は、末尾のテーブルで確認します。
- Number of Obs.: 分析に使用された観測数(生徒数)です。全体で
2000人のデータが使われ、カットオフ(80点)未満の生徒が1180人、以上の生徒が820人いることがわかります。 - テーブル “Robust Inference”:
- RD Effect (Point Estimate): これが主要な推定値です。
4.990と表示されており、「特進クラスに参加することにより、生徒の模試の偏差値は平均で約4.99ポイント向上する」と解釈でき、データ生成時に設定した真の因果効果(5ポイント)に近い結果です。 - P>|z| (p-value): p値です。
0.000となっており、この効果が統計的に有意(5%)であることを示しています。 - [ 95% C.I. ] (95% Confidence Interval):
[3.433, 6.270]は推定された因果効果の95%信頼区間です。
- RD Effect (Point Estimate): これが主要な推定値です。
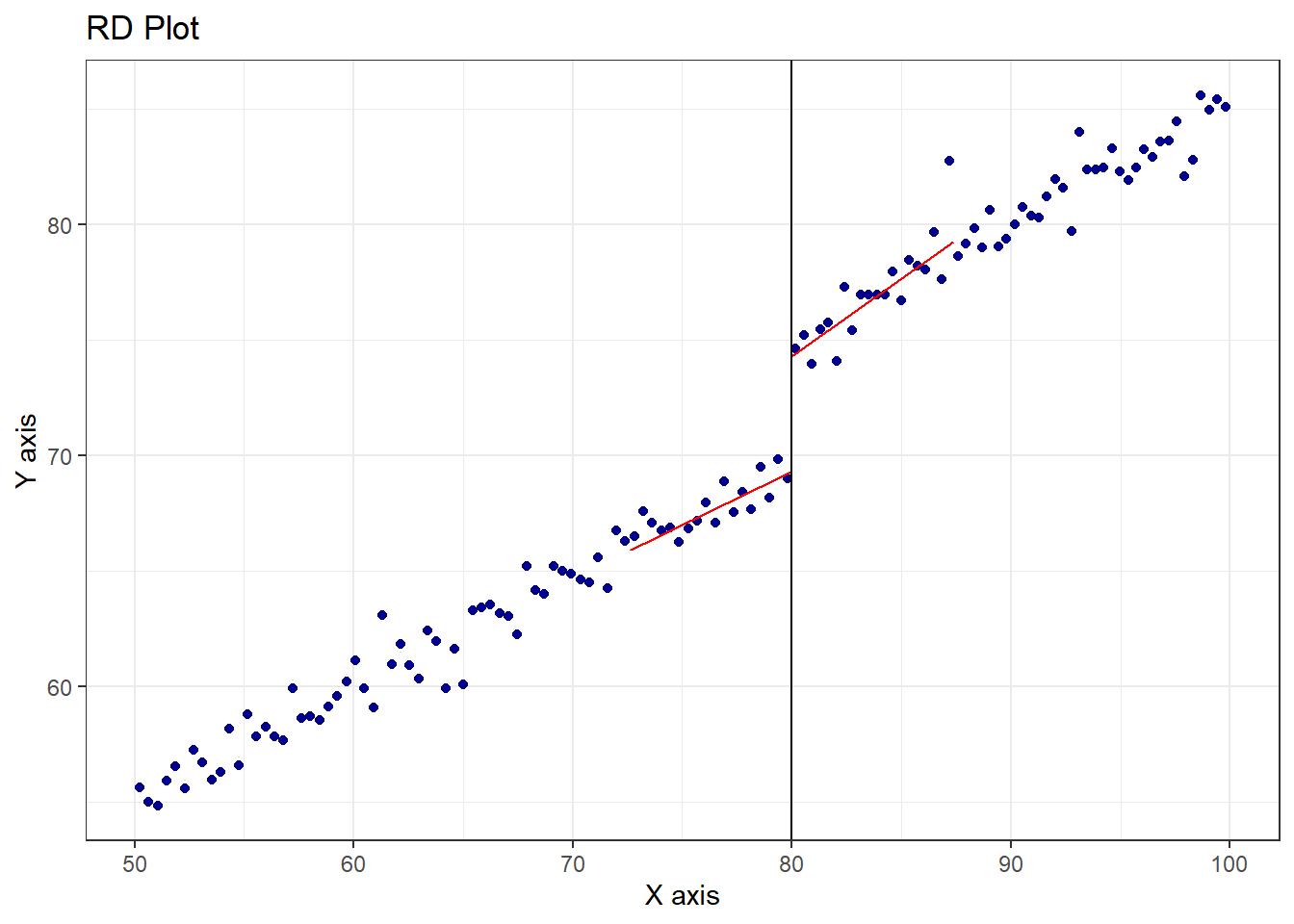
3.3. 結果の可視化
最後に、このRDD分析の結果を可視化します。
rdplot_obj <- rdplot(
y = sim_data_rdd$score_mock,
x = sim_data_rdd$score_entrance,
c = cutoff,
p = 1,
kernel = "tri",
h = 7.362
)
rdplot_obj$N
rdplot_obj$N_h
rdplot_obj$coef
rdplot_obj$coef[1, 2] - rdplot_obj$coef[1, 1][1] 1180 820
[1] 304 327
Left Right
[1,] 69.3011979 74.2911523
[2,] 0.4618448 0.6714796
Right
4.989954 以上です。