Rで 金融工学:現代ポートフォリオ理論 を試みます。
1. 現代ポートフォリオ理論の解説
現代ポートフォリオ理論は、1952年に経済学者ハリー・マーコウィッツによって提唱された、金融資産への投資におけるポートフォリオ(資産の組み合わせ)の最適な選択方法に関する理論です。この功績により、彼は1990年にノーベル経済学賞を受賞しました。
この理論の核心は「分散投資」の重要性を定量的に示した点にあります。
基本的な考え方
「卵は一つのカゴに盛るな(Don’t put all your eggs in one basket.)」という格言は有名ですが、現代ポートフォリオ理論は、なぜ、そしてどのように分散すれば最も効果的なのかを理論的に説明します。
重要なのは、個々の資産の「リターン」と「リスク」だけを見るのではなく、ポートフォリオ全体のリターンとリスクを考慮することです。
重要な3つの要素
- 期待リターン(Expected Return)
- その資産やポートフォリオから将来得られると期待されるリターンの平均値です。
- ポートフォリオ全体の期待リターンは、組み入れた各資産の期待リターンを、その構成比率(ウェイト)で加重平均したものになります。
- リスク(Risk)
- リターンの不確実性(ばらつき)を指し、一般的に標準偏差(または分散)で測定されます。
- ポートフォリオ全体のリスクは、各資産のリスクを加重平均したものではなく、各資産間の値動きの関連性、すなわち相関に大きく影響されます。
- 相関(Correlation)
- 2つの資産の値動きがどの程度連動するかを示す指標です。
- 負の相関を持つ(または相関が低い)資産同士を組み合わせることで、一方の資産が値下がりした際に、もう一方が値上がり(または影響を受けない)するため、ポートフォリオ全体のリターンの変動を抑えることができます。
- これにより、ポートフォリオ全体のリスクを、各資産のリスクの単純な加重平均よりも低くすることが可能になります。これが分散投資の最も重要な効果です。
効率的フロンティアと最適ポートフォリオ
- 効率的フロンティア(Efficient Frontier)
- 縦軸に「期待リターン」、横軸に「リスク(標準偏差)」をとったグラフを考えます。
- 考えられる多数のポートフォリオをプロットしていくと、点の集合ができます。
- この中で、「同じリスクの水準で、最も高いリターンが期待できるポートフォリオ」の集合を結んだ曲線のことを「効率的フロンティア」と呼びます。
- 合理的な投資家は、この曲線上のどこかのポートフォリオを選択するはずだと考えられます。
- 最適ポートフォリオ(Optimal Portfolio)
- 効率的フロンティア上のどの点を選ぶかは、その投資家がどれだけリスクを許容できるか(リスク許容度)によって決まります。
- 一般的には、シャープ・レシオという指標が最大になるポートフォリオが、最も効率的なポートフォリオ(接点ポートフォリオ)とされます。
- シャープ・レシオ = (ポートフォリオの期待リターン – 無リスク資産のリターン) / ポートフォリオのリスク
- これは「リスク1単位あたりで得られる超過リターン」を示し、この値が高いほど効率的な投資であることを意味します。
2. R言語によるシミュレーション
それでは、実際にR言語を使って現代ポートフォリオ理論をシミュレーションしてみましょう。 ここでは、複数の米国ハイテク株の過去の株価データを用いて、モンテカルロ・シミュレーションにより多数のポートフォリオを生成し、効率的フロンティアを可視化します。
ステップ1:準備
まず、シミュレーションに必要なパッケージを読み込みます。
# パッケージの読み込み
library(quantmod)
library(PerformanceAnalytics)
library(ggplot2)
library(dplyr)ステップ2:株価データの取得とリターンの計算
4つの銘柄(Apple, Microsoft, Google, Amazon)の過去5年間の株価データを取得し、日次リターンを計算します。
# 銘柄シンボル
tickers <- c("AAPL", "MSFT", "GOOG", "AMZN")
# データの取得期間
start_date <- "2019-01-01"
end_date <- "2023-12-31"
# Yahoo Financeから株価データを取得
getSymbols(tickers, src = "yahoo", from = start_date, to = end_date)
# 各銘柄の調整後終値を結合
prices <- do.call(merge, lapply(tickers, function(x) Ad(get(x))))
colnames(prices) <- tickers
# 日次リターンを計算
returns <- na.omit(Return.calculate(prices, method = "log"))
head(returns)[1] "AAPL" "MSFT" "GOOG" "AMZN"
AAPL MSFT GOOG AMZN
2019-01-03 -0.104924147 -0.037481944 -0.028897530 -0.025565529
2019-01-04 0.041803331 0.045459951 0.052389516 0.048851113
2019-01-07 -0.002228252 0.001274738 -0.002169208 0.033776511
2019-01-08 0.018883760 0.007224496 0.007357829 0.016475884
2019-01-09 0.016838899 0.014198347 -0.001506233 0.001712887
2019-01-10 0.003191115 -0.006446205 -0.004037405 -0.001930291ステップ3:モンテカルロ・シミュレーションの実行
ランダムな資産配分(ウェイト)を持つポートフォリオを多数(ここでは10,000個)生成し、それぞれの期待リターン、リスク(標準偏差)、シャープ・レシオを計算します。
# シミュレーション回数
num_portfolios <- 10000
# 年率換算の期待リターンと共分散行列
mean_ret <- colMeans(returns) * 252
cov_mat <- cov(returns) * 252
# 結果を格納するデータフレームを初期化
portfolio_results <- data.frame(
returns = numeric(num_portfolios),
risk = numeric(num_portfolios),
sharpe_ratio = numeric(num_portfolios)
)
# 各ポートフォリオのウェイトを格納する行列
weights_matrix <- matrix(nrow = num_portfolios, ncol = length(tickers))
colnames(weights_matrix) <- tickers
# 無リスク金利(ここでは仮に2% = 0.02と設定)
risk_free_rate <- 0.02
# シミュレーションのループ
seed <- 20250822
set.seed(seed)
for (i in 1:num_portfolios) {
# 1. ランダムなウェイトを生成
weights <- runif(length(tickers))
weights <- weights / sum(weights) # 合計が1になるように正規化
weights_matrix[i, ] <- weights
# 2. ポートフォリオの期待リターンを計算
port_return <- sum(weights * mean_ret)
portfolio_results$returns[i] <- port_return
# 3. ポートフォリオのリスク(標準偏差)を計算
port_risk <- sqrt(t(weights) %*% cov_mat %*% weights)
portfolio_results$risk[i] <- port_risk
# 4. シャープ・レシオを計算
sharpe <- (port_return - risk_free_rate) / port_risk
portfolio_results$sharpe_ratio[i] <- sharpe
}
# ポートフォリオのウェイトも結果に結合
all_results <- bind_cols(as.data.frame(weights_matrix), portfolio_results)
head(all_results) AAPL MSFT GOOG AMZN returns risk sharpe_ratio
1 0.34767200 0.2906976 0.27533692 0.08629350 0.2593451 0.2840316 0.8426707
2 0.35426183 0.1482858 0.33007462 0.16737776 0.2444555 0.2848720 0.7879171
3 0.03044032 0.8695305 0.03701552 0.06301364 0.2638367 0.2976641 0.8191673
4 0.14159295 0.4363540 0.05271849 0.36933456 0.2264048 0.2909406 0.7094397
5 0.36082004 0.4481363 0.13827723 0.05276646 0.2749028 0.2863384 0.8902153
6 0.23852251 0.2367760 0.26505390 0.25964755 0.2306167 0.2847904 0.7395500ステップ4:結果の可視化と最適ポートフォリオの特定
シミュレーション結果をプロットして効率的フロンティアを可視化し、「シャープ・レシオ最大ポートフォリオ」と「リスク最小ポートフォリオ」を特定します。
# シャープ・レシオが最大のポートフォリオを特定
max_sharpe_portfolio <- all_results[which.max(all_results$sharpe_ratio), ]
# リスクが最小のポートフォリオを特定
min_risk_portfolio <- all_results[which.min(all_results$risk), ]
# ggplot2で可視化
p <- ggplot(all_results, aes(x = risk, y = returns, color = sharpe_ratio)) +
geom_point(alpha = 0.5) +
scale_color_gradient(low = "blue", high = "red") + # シャープ・レシオを色で表現
labs(
title = "現代ポートフォリオ理論:効率的フロンティアのシミュレーション",
x = "リスク(年率標準偏差)",
y = "期待リターン(年率)",
color = "シャープ・レシオ"
) +
theme_minimal() +
# シャープ・レシオ最大のポートフォリオをプロット
geom_point(data = max_sharpe_portfolio, aes(x = risk, y = returns), color = "magenta", size = 5, shape = 18) +
annotate("text", x = 0.31, y = max_sharpe_portfolio$returns, label = "シャープ・レシオ最大", color = "magenta", hjust = 0) +
# リスク最小のポートフォリオをプロット
geom_point(data = min_risk_portfolio, aes(x = risk, y = returns), color = "green", size = 5, shape = 18) +
annotate("text", x = 0.31, y = min_risk_portfolio$returns, label = "リスク最小", color = "green", hjust = 0)
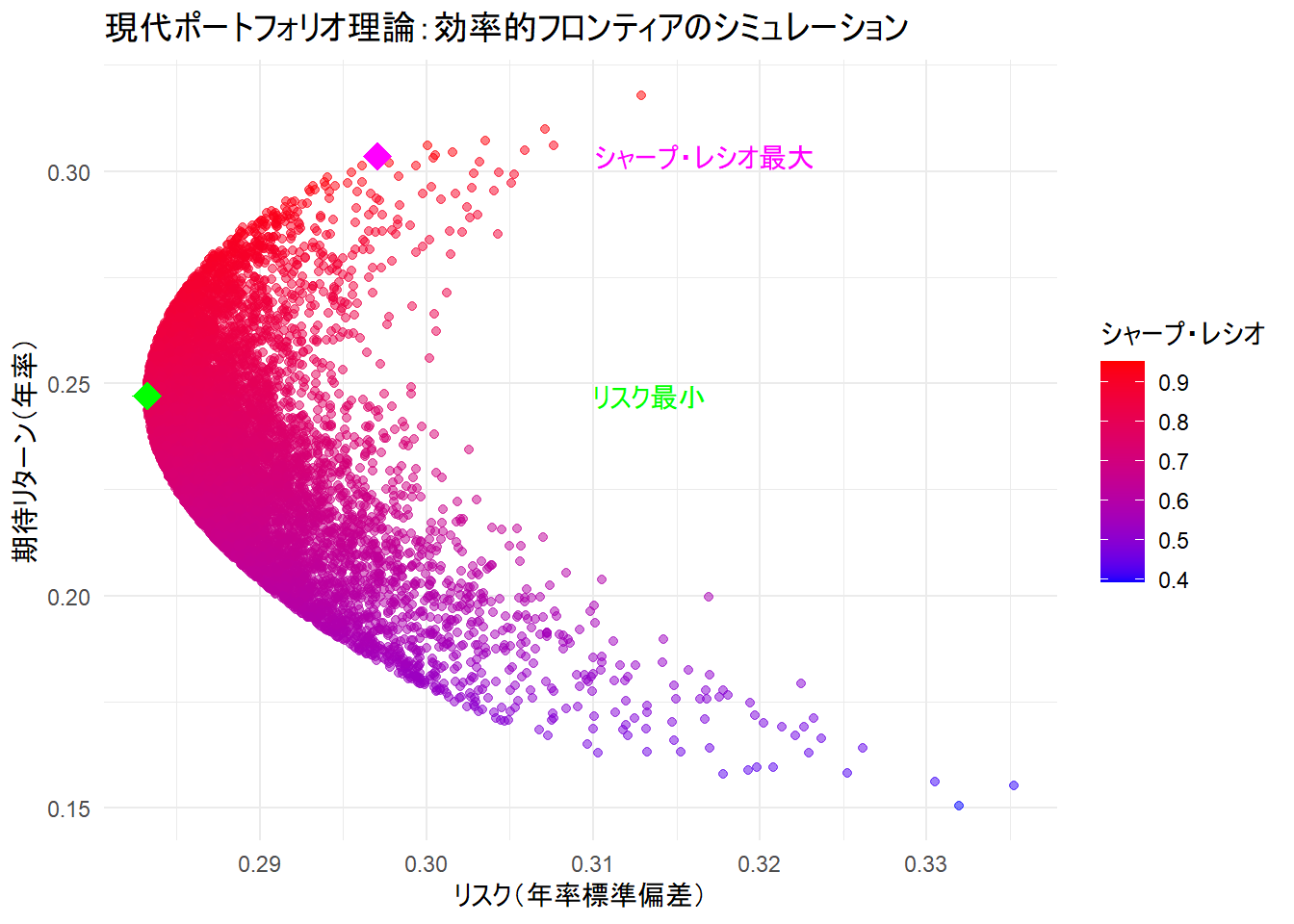
print(p)Figure 1 の解説
1. グラフの全体像:リスクとリターンの世界
- 横軸 (X軸): ポートフォリオのリスク(年率標準偏差)を表します。右に行くほどリスクが高く(価格変動が大きく)、左に行くほどリスクが低い(価格変動が小さい)ことを意味します。
- 縦軸 (Y軸): ポートフォリオの期待リターン(年率)を表します。上に行くほど期待できるリターンが高く、下に行くほどリターンが低いことを意味します。
2. 各点の意味:無数のポートフォリオ
グラフ上にプロットされた一つ一つの点が、それぞれ異なる資産配分(ウェイト)を持つ1つのポートフォリオを表しています。今回は10,000個のポートフォリオをシミュレーションしましたので、ここには10,000個の点が存在します。
3. 色の意味:シャープ・レシオ(投資効率)
点の色は、そのポートフォリオのシャープ・レシオ(投資効率)を示しています。
- 赤色に近いほど: シャープ・レシオが高く、取ったリスクに対して得られるリターンが大きい「効率の良い」ポートフォリオであることを示します。
- 青色に近いほど: シャープ・レシオが低く、「効率の悪い」ポートフォリオであることを示します。
4. 効率的フロンティア
点の集合のリスク最小点から上の境界線(フロンティア)に注目してください。この線は「効率的フロンティア」と呼ばれます。
この線上にあるポートフォリオは、最も効率的なポートフォリオの集まりです。なぜなら、
- 同じリスク水準(横軸の同じ位置)で比較した場合、この線上のポートフォリオが最も高いリターンを提供します。
- 同じリターン水準(縦軸の同じ位置)で比較した場合、この線上のポートフォリオが最も低いリスクで済むからです。
合理的な投資家は、この効率的フロンティアの内側にある非効率なポートフォリオを選ぶことはなく、必ずこの線上のどこかを選ぶべきだと理論上は考えられます。
5. 2つの特別な点
Figure 1 には、特に重要な2つのポートフォリオが強調表示されています。
- マゼンタ色の菱形(シャープ・レシオ最大):
- これは、10,000個のポートフォリオの中でシャープ・レシオが最大となった点です。
- リスクとリターンのバランスが最も優れており、最も投資効率が良いポートフォリオと見なされます。多くの投資家にとっての最適解の一つです。
- 緑色の菱形(リスク最小):
- これは、リスク(標準偏差)が最も小さかったポートフォリオです。
- 効率的フロンティアの最も左端に位置し、最も価格変動が小さい安定志向のポートフォリオと言えます。リターンよりも安定性を最優先する投資家向けの選択肢です。
6. 結論
Figure 1 は、現代ポートフォリオ理論の「分散投資によって、同じリスクでもより高いリターンを、あるいは同じリターンならより低いリスクを目指すことができる」という考え方を視覚的に示しています。
投資家は、この「効率的フロンティア」の中から、自身のリスク許容度(どれだけリスクを受け入れられるか)に合ったポートフォリオ(例えば、「シャープ・レシオ最大」や「リスク最小」、あるいはその中間の点など)を選択することになります。
# 最適ポートフォリオの具体的なウェイトを表示
cat("--- シャープ・レシオ最大のポートフォリオ ---\n")
print(max_sharpe_portfolio)--- シャープ・レシオ最大のポートフォリオ ---
AAPL MSFT GOOG AMZN returns risk sharpe_ratio
6787 0.6330006 0.3297097 0.03013687 0.007152825 0.3034745 0.2970759 0.9542159この結果は、シミュレーションで生成した10,000個のポートフォリオの中で、「シャープ・レシオ」が最も高くなったポートフォリオを示しています。現代ポートフォリオ理論において、これは最も投資効率が良いとされるポートフォリオ(接点ポートフォリオ)を意味します。
各項目の意味は以下の通りです。
1. 資産配分(ウェイト)
-
AAPL: 0.6330… (約63.3%) -
MSFT: 0.3297… (約33.0%) -
GOOG: 0.0301… (約3.0%) -
AMZN: 0.0071… (約0.7%)
これは、ポートフォリオに組み入れる各銘柄の投資比率を表しています。 つまり、今回のシミュレーション期間(2019年〜2023年)のデータにおいては、「投資資金の約63%をAppleに、約33%をMicrosoftに、残りをGoogleとAmazonに少しずつ配分する」という組み合わせが、最も効率的であったことを示唆しています。
2. ポートフォリオの特性
-
returns: 0.3034745 (年率リターン: 約30.3%)- この資産配分で運用した場合に期待される年率リターンです。過去のデータに基づけば、年平均で約30.3%のリターンが見込めることを意味します。
-
risk: 0.2970759 (年率リスク: 約29.7%)- これはポートフォリオの年率リスク(標準偏差)です。リターンのばらつきの大きさを表しており、期待リターンから上下に約29.7%程度の変動が起こりうる可能性を示唆しています。
-
sharpe_ratio: 0.9542158 (シャープ・レシオ: 約0.95)- このポートフォリオのシャープ・レシオです。これは「取ったリスク1単位あたり、どれだけのリターン(無リスク金利を超過するリターン)を得られたか」を示す指標で、投資の効率性を測ります。
- この0.95という値が、シミュレーションした10,000通りの組み合わせの中で最も高い数値でした。
3. 結論として
この結果が示しているのは、「2019年から2023年の市場において、AAPL、MSFT、GOOG、AMZNの4銘柄に投資するなら、AppleとMicrosoftに重点を置いたポートフォリオ(AAPL: 63%, MSFT: 33%)が、リスクとリターンのバランスが最も優れた選択であった」ということです。
cat("--- リスク最小のポートフォリオ ---\n")
print(min_risk_portfolio)--- リスク最小のポートフォリオ ---
AAPL MSFT GOOG AMZN returns risk sharpe_ratio
8537 0.254947 0.3253241 0.2834265 0.1363024 0.2470328 0.2832383 0.8015609この結果は、シミュレーションで生成した10,000個のポートフォリオの中で、「リスク(年率標準偏差)」が最も低くなったポートフォリオを示しています。これは「グローバル最小分散ポートフォリオ(Global Minimum Variance Portfolio)」とも呼ばれ、リターンを問わず、とにかく価格変動を最小限に抑えたいと考える、リスク回避的な投資家にとっての最適な選択肢となります。
各項目の意味は以下の通りです。
1. 資産配分(ウェイト)
-
AAPL: 0.2549… (約25.5%) -
MSFT: 0.3253… (約32.5%) -
GOOG: 0.2834… (約28.3%) -
AMZN: 0.1363… (約13.6%)
これは、ポートフォリオを構成する各銘柄の投資比率です。 先ほどの「シャープ・レシオ最大ポートフォリオ」がAAPLとMSFTに大きく偏っていたのに対し、この「リスク最小ポートフォリオ」では、4つの銘柄により均等に近い形で資産を配分していることがわかります。これは、特定の資産への集中を避け、幅広く分散させることで、ポートフォリオ全体のリスクを低減するという分散投資の効果が最もよく表れた結果と言えます。
2. ポートフォリオの特性
-
returns: 0.2470328 (年率リターン: 約24.7%)- この資産配分で運用した場合に期待される年率リターンです。シャープ・レシオ最大ポートフォリオの期待リターン(約30.3%)と比較すると、やや低い水準になっています。これは、リスクを抑えるために、より高いリターンを犠牲にしていることを意味します(リスクとリターンのトレードオフ)。
-
risk: 0.2832383 (年率リスク: 約28.3%)- このポートフォリオの年率リスク(標準偏差)です。この0.2832という値が、シミュレーションした10,000通りの組み合わせの中で最も低い数値でした。つまり、この資産配分が最も価格変動の小さい組み合わせであったことを示しています。
-
sharpe_ratio: 0.801561 (シャープ・レシオ: 約0.80)- このポートフォリオのシャープ・レシオです。シャープ・レシオ最大ポートフォリオ(約0.95)よりも低い値となっており、投資効率(リスクあたりのリターン)の観点では劣ることを示しています。しかし、このポートフォリオの目的は効率性ではなく、あくまでリスクの最小化にあります。
3. 結論として
この結果が示しているのは、「2019年から2023年の市場において、AAPL、MSFT、GOOG、AMZNの4銘柄に投資するなら、4銘柄を比較的バランス良く組み合わせることが、ポートフォリオ全体のリスクを最も小さくする戦略であった」ということです。
「シャープ・レシオ最大ポートフォリオ」とこの「リスク最小ポートフォリオ」は、効率的フロンティアという曲線上の代表的な2点です。どちらを選ぶべきかは、投資家自身がどれだけのリスクを許容できるか(リスク許容度)によって決まります。 より高いリターンを目指すなら前者、安定性を最優先するなら後者が、合理的な選択肢となります。
(参考)効率的フロンティアの近似曲線
# 最適化計算用のパッケージを読み込み
library(quadprog)
# 効率的フロンティアを計算するためのターゲットリターン範囲を設定
# リスク最小ポートフォリオのリターンから、シミュレーション中の最大リターンまでを100分割
target_returns <- seq(
min_risk_portfolio$returns,
max(all_results$returns),
length.out = 100
)
# フロンティア上のポートフォリオのリスクを格納するベクトル
frontier_risk <- numeric(length(target_returns))
# 各ターゲットリターンに対してリスクを最小化するポートフォリオを計算
for (i in 1:length(target_returns)) {
target_ret <- target_returns[i]
# 最適化問題を解くための制約条件を設定
# 1. ウェイトの合計が1
# 2. ポートフォリオの期待リターンがターゲットリターンと一致
# 3. 各ウェイトは0以上
constraints_mat <- cbind(
rep(1, length(tickers)), # ウェイトの合計
mean_ret, # 期待リターン
diag(length(tickers)) # 各ウェイト >= 0
)
constraints_vec <- c(
1, # ウェイトの合計 = 1
target_ret, # 期待リターン = target_ret
rep(0, length(tickers)) # 各ウェイト >= 0
)
# solve.QP関数で二次計画問題を解く
# tryCatchでエラー(解が存在しない場合など)を処理
sol <- tryCatch(
{
solve.QP(
Dmat = 2 * cov_mat,
dvec = rep(0, length(tickers)),
Amat = constraints_mat,
bvec = constraints_vec,
meq = 2 # 最初の2つが等式制約
)
},
error = function(e) NULL
)
if (!is.null(sol)) {
# 最適なウェイトを使ってポートフォリオのリスクを計算
optimal_weights <- sol$solution
frontier_risk[i] <- sqrt(t(optimal_weights) %*% cov_mat %*% optimal_weights)
} else {
frontier_risk[i] <- NA # 解がない場合はNA
}
}
# 結果をデータフレームにまとめる
frontier_points <- data.frame(
returns = target_returns,
risk = frontier_risk
) %>% na.omit() # 解がなかった点を除外
# 元のプロットに効率的フロンティアの線を追加
p_with_frontier <- p +
geom_line(
data = frontier_points,
aes(x = risk, y = returns), # 凡例の色分けを継承しないようにaesをここで指定
color = "blue",
linewidth = 1.2
) +
labs(title = "現代ポートフォリオ理論:効率的フロンティア")
# 最終的なグラフを表示
print(p_with_frontier)以上です。