Rの関数から rdrobust {rdrobust} を確認します。
1. rdrobust関数の目的と概要
回帰不連続デザイン(RDD)は、あるカットオフ(閾値)を境に処置(介入)の有無が割り当てられる状況を利用して、その処置の効果を推定する分析手法です。例えば、特定の試験スコア以上で奨学金が給付される場合、そのスコア周辺の学生を比較することで奨学金の効果を測ることができます。
rdrobust関数は、このRDD分析を頑健(robust)に行うために、Calonico, Cattaneo, Titiunik (2014) らによって開発された統計手法を実装しています。主な特徴は以下の通りです。
- 局所多項式回帰: カットオフ近傍のデータのみを用いて、柔軟な回帰モデル(線形、二次など)を当てはめます。
- 最適なバンド幅選択: 推定の精度を左右する「カットオフからどれくらいの範囲のデータを使うか(バンド幅)」を、平均二乗誤差(MSE)やカバレッジ誤差(CER)を最小化するように自動で選択します。
- バイアス補正: 局所多項式回帰に伴うバイアスを補正した推定値を算出します。
- 頑健な標準誤差: 不均一分散やクラスター構造に対応した標準誤差と信頼区間を提供します。
- シャープRDDとファジーRDDへの対応: 処置がカットオフで完全に決まるシャープRDDだけでなく、処置確率がジャンプするファジーRDDにも対応しています。
2. 基本的な使い方(最小限の引数)
最もシンプルにrdrobust関数を使うには、3つの引数を指定します。
-
y: 結果変数 (Outcome Variable)。処置によって影響を受けると想定される変数です。 -
x: 割り当て変数 (Running Variable / Score)。処置の割り当てを決める連続変数です。 -
c: カットオフ (Cutoff)。xがこの値を超えると処置の有無が変わる閾値です。
例:架空データでの分析
# パッケージをロード
library(rdrobust)
# 架空のデータを作成
seed <- 20250827
set.seed(seed)
n <- 1000
# 割り当て変数 x (-1から1の範囲)
x <- runif(n, -1, 1)
# カットオフ c=0 で処置が決まる (Sharp RDD)
d <- ifelse(x >= 0, 1, 0)
# 結果変数 y (処置効果=5のジャンプがある)
y <- 1 + 2 * x + 5 * d + rnorm(n)
# rdrobustを実行
# yとxを指定し、カットオフc=0を設定
fit <- rdrobust(y = y, x = x, c = 0)
# 結果の要約を表示
summary(fit)Sharp RD estimates using local polynomial regression.
Number of Obs. 1000
BW type mserd
Kernel Triangular
VCE method NN
Number of Obs. 484 516
Eff. Number of Obs. 138 158
Order est. (p) 1 1
Order bias (q) 2 2
BW est. (h) 0.299 0.299
BW bias (b) 0.499 0.499
rho (h/b) 0.599 0.599
Unique Obs. 484 516
=====================================================================
Point Robust Inference
Estimate z P>|z| [ 95% C.I. ]
---------------------------------------------------------------------
RD Effect 4.969 15.037 0.000 [4.266 , 5.545]
=====================================================================この結果から、処置効果が約4.97であり、かつ有意(5%。以下同様)であることがわかります。(詳細は「4. 結果(出力)の解釈」で解説します)
3. 主要な引数の詳細解説
rdrobustは多くの引数を持ちますが、ここでは特に重要なものを機能別に解説します。
(1) 分析の基本設定
-
y,x,c: 上述の通り、結果変数、割り当て変数、カットオフです。 -
fuzzy: ファジーRDDの場合に、実際の処置状況を示す変数(0か1)を指定します。指定すると、rdrobustは自動的にファジーRDDの分析(操作変数法に似た推定)を行います。 -
deriv: 推定したい導関数の階数を指定します。-
deriv = 0(デフォルト): 結果変数yの水準のジャンプ、つまり処置効果を推定します。 -
deriv = 1: 回帰関数の傾き(slope)のジャンプを推定します。これはKink RDDと呼ばれます。
-
-
p: 局所回帰に用いる多項式の次数 (polynomial order) です。-
p = 1(デフォルト): 局所線形回帰。直線で近似します。 -
p = 2: 局所二次回帰。放物線で近似します。 -
p = 0: 局所定数回帰。
-
(2) バンド幅の選択
-
h,b: バンド幅を手動で指定したい場合に使います。hは主要な推定、bはバイアス補正用です。 -
bwselect: バンド幅の自動選択アルゴリズムを指定します。これがrdrobustの核となる機能の一つです。-
"mserd"(デフォルト): RD効果の推定量の平均二乗誤差 (Mean Squared Error) を最小化するバンド幅を選択します。デフォルトの選択肢です。 -
"cerrd": カバレッジ誤差 (Coverage Error Rate) を考慮したバンド幅を選択します。 - その他、
"msetwo","msesum","msecomb1","msecomb2"など、異なる基準や複数の基準を組み合わせた手法も用意されており、頑健性チェックに利用できます。
-
(3) カーネル関数と重み付け
-
kernel: 局所回帰の際に、カットオフに近い点に大きな重みを与えるためのカーネル関数を指定します。-
"tri"または"triangular"(デフォルト): 三角カーネル。 -
"uni"または"uniform": 矩形(一様)カーネル。バンド幅内の全ての点に同じ重みを与えます。 -
"epa"または"epanechnikov": エパネチニコフカーネル。
-
-
weights: 各観測値に個別の重みを付けたい場合に、そのベクトルを指定します。
(4) 分散推定と信頼区間
-
vce: 標準誤差の計算方法(分散共分散行列の推定方法)を指定します。-
"nn"(デフォルト): 最近傍法 (Nearest Neighbor) に基づく分散推定量。 -
"hc0","hc1","hc2","hc3": 不均一分散に対して頑健な標準誤差(いわゆるWhiteの標準誤差)。
-
-
cluster: クラスター頑健標準誤差を計算したい場合に、クラスターIDを示すベクトルを指定します。例えば、生徒レベルのデータで学校ごとに誤差の相関が疑われる場合などに使用します。 -
level: 信頼区間の信頼水準をパーセントで指定します。デフォルトは95です。
(5) 共変量の調整
-
covs: 共変量(年齢、性別など、処置以外の変数)を含める場合に、行列またはデータフレームで指定します。共変量を含めることで、推定の精度(効率性)を高める効果が期待できます。 -
covs_drop:TRUE(デフォルト) の場合、共変量間に多重共線性がある場合は自動的に変数を除去します。
4. 結果(出力)の解釈
(1) 上部の情報エリア
Sharp RD estimates using local polynomial regression.
Number of Obs. 1000
BW type mserd
Kernel Triangular
VCE method NN-
Sharp RD estimates...: 分析の種類がシャープRDDであることが示されています。 -
Number of Obs.: 全体の観測点数が1000であることを示します。 -
BW type,Kernel,VCE method: バンド幅選択法(mserd)、カーネル関数(Triangular)、分散推定法(NN)が、それぞれデフォルト設定で実行されたことを示します。
(2) 詳細なパラメータエリア
Number of Obs. 484 516
Eff. Number of Obs. 138 158
Order est. (p) 1 1
Order bias (q) 2 2
BW est. (h) 0.299 0.299
BW bias (b) 0.499 0.499
rho (h/b) 0.599 0.599
Unique Obs. 484 516このエリアは、カットオフの左側(1列目)と右側(2列目)それぞれの情報を表示しています。
-
Number of Obs.: カットオフの左側に484、右側に516の観測点があることを示します。 -
Eff. Number of Obs.: カーネルの重みを考慮した実質的な観測点数。左側138、右側158。 -
Order est. (p): 推定に使われた局所多項式の次数。ここでは両側とも線形(1次)です。 -
Order bias (q): バイアス補正に使われた局所多項式の次数。ここでは両側とも二次(2次)です。 -
BW est. (h): 主要な推定に使用されたバンド幅。ここでは両側とも0.299です。 -
BW bias (b): バイアス補正に使用されたバンド幅。ここでは両側とも0.499です。
(3) 推定結果エリア
=====================================================================
Point Robust Inference
Estimate z P>|z| [ 95% C.I. ]
---------------------------------------------------------------------
RD Effect 4.969 15.037 0.000 [4.266 , 5.545]
=====================================================================RD Effectの行は、バイアス補正済みの推定値と、頑健な標準誤差に基づく推定結果を示しています。
-
Point Estimate: 推定された処置効果(カットオフでのジャンプの大きさ)。推定結果は4.969と設定した5に近い処置効果が推定できています。 -
z: z値(15.037)。Point Estimateを標準誤差で割った値で、効果の大きさを示します。 -
P>|z|: p値(0.000)。処置効果が0であるという帰無仮説を検定します。5%以下であるため、処置効果は有意であると結論できます。 -
[ 95% C.I. ]: 処置効果の95%信頼区間([4.266 , 5.545])です。
結論の要約: この分析結果は、「カットオフ点において、処置によって結果変数が平均して約4.97増加する効果があり、この効果は統計的に有意である」ことを示唆しています。
5. 実践的なヒントと応用例
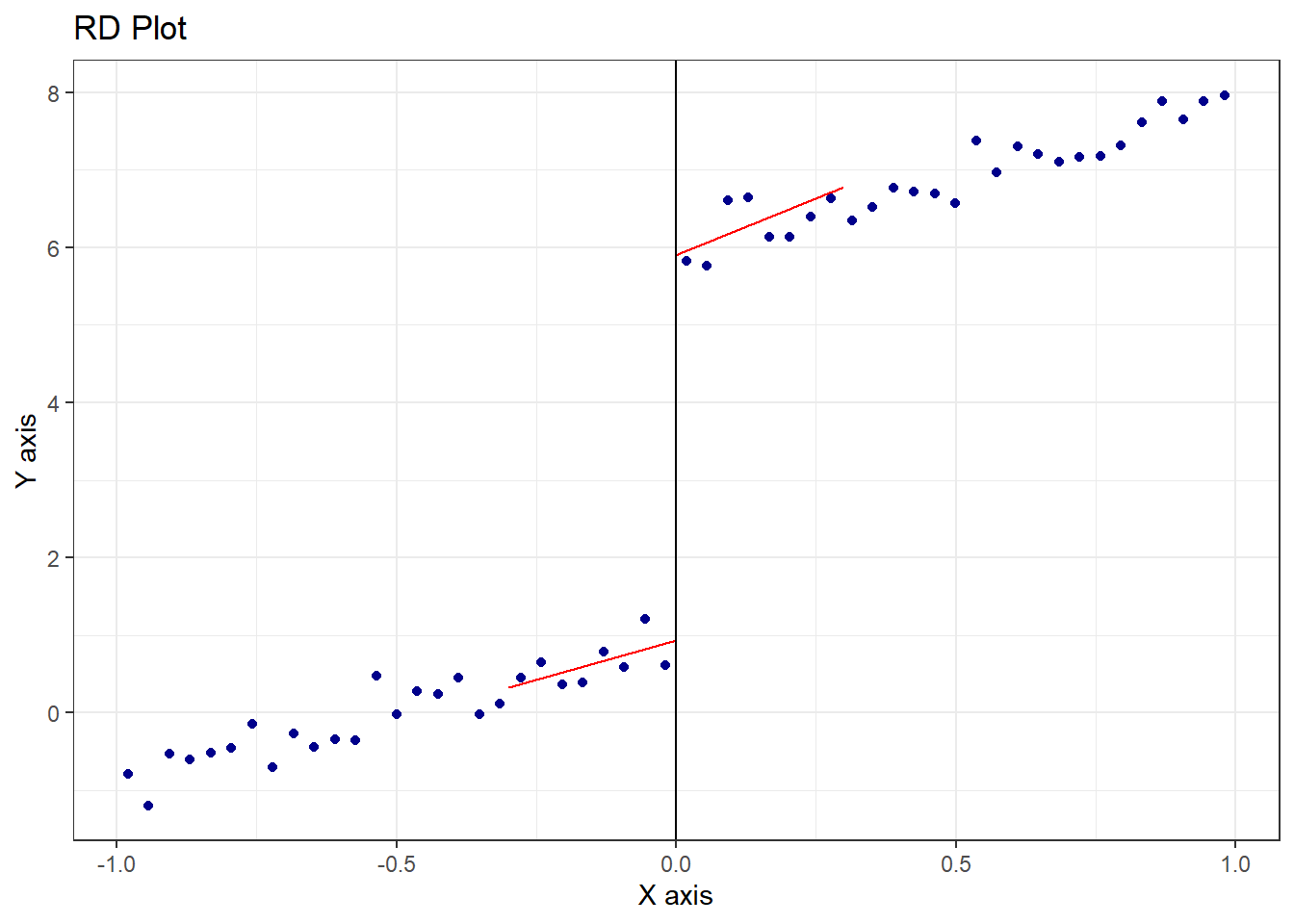
(1) 可視化
カットオフ点でのジャンプを視覚的に確認します。
args(rdrobust)
args(rdplot)function (y, x, c = NULL, fuzzy = NULL, deriv = NULL, p = NULL,
q = NULL, h = NULL, b = NULL, rho = NULL, covs = NULL, covs_drop = TRUE,
ginv.tol = 1e-20, kernel = "tri", weights = NULL, bwselect = "mserd",
vce = "nn", cluster = NULL, nnmatch = 3, level = 95, scalepar = 1,
scaleregul = 1, sharpbw = FALSE, detail = NULL, all = NULL,
subset = NULL, masspoints = "adjust", bwcheck = NULL, bwrestrict = TRUE,
stdvars = FALSE)
NULL
function (y, x, c = 0, p = 4, nbins = NULL, binselect = "esmv",
scale = NULL, kernel = "uni", weights = NULL, h = NULL, covs = NULL,
covs_eval = "mean", covs_drop = TRUE, ginv.tol = 1e-20, support = NULL,
subset = NULL, masspoints = "adjust", hide = FALSE, ci = NULL,
shade = FALSE, title = NULL, x.label = NULL, y.label = NULL,
x.lim = NULL, y.lim = NULL, col.dots = NULL, col.lines = NULL)
NULL(2) ファジーRDD
もし処置がカットオフで完全には決まらず、処置を受ける確率がジャンプするだけの場合(ファジーRDD)、fuzzy引数を指定します。
set.seed(seed)
n <- 1000
x <- runif(n, -1, 1) # 割り当て変数
c <- 0 # カットオフ
# --- ファジーRDDのキーポイント ---
# カットオフを境に「処置を受ける確率」がジャンプする状況を作る
# x < 0 の人は20%の確率で、x >= 0 の人は80%の確率で処置を受ける
prob_treat <- ifelse(x < c, 0.2, 0.8)
# 上記の確率に基づいて、実際に処置を受けたか(1)、受けなかったか(0)の変数を作成
actual_treatment <- rbinom(n, 1, prob_treat)
# 結果変数yを作成(処置効果は5とする)
y <- 1 + 2 * x + 5 * actual_treatment + rnorm(n)
# fuzzy引数に、先ほど作成した実在する変数 'actual_treatment' を渡す
fit_fuzzy <- rdrobust(y = y, x = x, c = 0, fuzzy = actual_treatment)
summary(fit_fuzzy)Fuzzy RD estimates using local polynomial regression.
Number of Obs. 1000
BW type mserd
Kernel Triangular
VCE method NN
Number of Obs. 484 516
Eff. Number of Obs. 119 136
Order est. (p) 1 1
Order bias (q) 2 2
BW est. (h) 0.255 0.255
BW bias (b) 0.430 0.430
rho (h/b) 0.594 0.594
Unique Obs. 484 516
First-stage estimates.
=====================================================================
Point Robust Inference
Estimate z P>|z| [ 95% C.I. ]
=====================================================================
Rd Effect 0.695 5.216 0.000 [0.437 , 0.963]
=====================================================================
Treatment effect estimates.
=====================================================================
Point Robust Inference
Estimate z P>|z| [ 95% C.I. ]
---------------------------------------------------------------------
RD Effect 5.083 10.462 0.000 [4.175 , 6.101]
=====================================================================1. 分析の概要:ファジー回帰不連続デザイン (Fuzzy RDD)
まず、Fuzzy RD estimates using local polynomial regression. という最初の行が、これがファジーRDDの分析であることを示しています。
ファジーRDDは、カットオフを越えても処置を受けるかどうかが100%決まるわけではなく、処置を受ける「確率」がジャンプする状況を分析します。この分析は、以下の2つのステップで因果効果を推定します。
- 第一段階 (First-stage): カットオフを越えることで、実際に処置を受ける確率がどれだけ上昇したか?
- 第二段階 (Treatment effect): 結果変数(y)のジャンプを、第一段階で推定した処置確率のジャンプで割ることで、処置そのものの因果効果を算出する。
2.結果の各エリアの詳細解説
1. 上部・詳細パラメータエリア
Number of Obs. 1000
BW type mserd
Kernel Triangular
VCE method NN
Number of Obs. 484 516
Eff. Number of Obs. 119 136
Order est. (p) 1 1
Order bias (q) 2 2
BW est. (h) 0.255 0.255
BW bias (b) 0.430 0.430
rho (h/b) 0.594 0.594
Unique Obs. 484 516このエリアはシャープRDDの時と同様、分析の基本設定を示しています。
-
Number of Obs.: 観測点数(左側484、右側516)。 -
BW est. (h): 推定に使用されたバンド幅(0.255)。 -
Order est. (p): 局所線形回帰(次数1)が使用されたことを示します。
2. 第一段階の推定 (First-stage estimates)
First-stage estimates.
=====================================================================
Point Robust Inference
Estimate z P>|z| [ 95% C.I. ]
=====================================================================
Rd Effect 0.695 5.216 0.000 [0.437 , 0.963]
=====================================================================【このエリアの目的】
ここは「カットオフを越えることが、実際に処置を受ける確率にどれだけ影響を与えたか」を検証する部分です。カットオフ(x=0)を一種の「操作変数」とみなし、それが処置変数(actual_treatment)に与える効果を推定しています。
【結果の解釈】
-
Point Estimate: 0.695- これは、カットオフ点において、処置を受ける確率が約0.695(69.5パーセントポイント)ジャンプしたことを意味します。(シミュレーションでは0.2→0.8へのジャンプ、つまり0.6の差を設定しましたので、それに近い値が推定されています。)
-
z値 (5.216) とP>|z|(0.000)- この処置確率のジャンプが、統計的に有意であることを示しています。
3. 処置効果の推定 (Treatment effect estimates)
Treatment effect estimates.
=====================================================================
Point Robust Inference
Estimate z P>|z| [ 95% C.I. ]
---------------------------------------------------------------------
RD Effect 5.083 10.462 0.000 [4.175 , 6.101]
=====================================================================【このエリアの目的】
こちらが最終的に知りたかった「処置そのものが結果変数(y)に与えた因果効果」です。LATE (Local Average Treatment Effect) と呼ばれ、「カットオフ近傍にいて、カットオフを越えたことで処置を受けることになった人々」に対する平均的な処置効果を示します。
この値は、おおまかに言いますと (結果変数yのジャンプ) / (処置確率のジャンプ) で計算されます。
【結果の解釈】
-
Point Estimate: 5.083- これが、この分析の主たる結論です。処置を受けたことによる結果変数への因果効果は、平均して約5.083であると推定されます。(シミュレーションで設定した真の効果
5に近い値です。)
- これが、この分析の主たる結論です。処置を受けたことによる結果変数への因果効果は、平均して約5.083であると推定されます。(シミュレーションで設定した真の効果
-
z値 (10.462) とP>|z|(0.000)- この処置効果は、統計的に有意であると結論できます。
-
[ 95% C.I. ]:[4.175 , 6.101]- 処置効果の95%信頼区間です。
3. 総合的な結論
このファジーRDD分析の結果は、以下のように要約できます。
「カットオフ点において、処置を受ける確率は約69.5パーセントポイント上昇した(第一段階)。この処置確率の上昇を考慮すると、処置そのものによる因果効果は、結果変数を約5.08増加させるものであり、この効果は統計的に有意である。」
(3) 頑健性チェック
分析の信頼性を高めるために、異なる多項式の次数 (p=2) や異なるバンド幅選択法 (bwselect="cerrd") を試して、結果が大きく変わらないかを確認したり、処置効果がないはずの場所(例えばc=0.5)で分析を行い、効果が検出されないことを確認する(Placebo Test)等が推奨されます。
6. パラメトリックRDDの模倣とlmによる比較
ステップ1: サンプルデータの準備
まず、以前の例と同様のシャープRDDのサンプルデータを再作成します。
# サンプルデータを再作成
set.seed(seed)
n <- 1000
c <- 0 # カットオフ
# 割り当て変数 x (-1から1の範囲)
x <- runif(n, -1, 1)
# カットオフ c=0 で処置が決まる (Sharp RDD)
# この D が lm() で使う処置ダミー変数になります
D <- ifelse(x >= c, 1, 0)
# 結果変数 y (処置効果=5のジャンプがある)
y <- 1 + 2 * x + 5 * D + rnorm(n)ステップ2: rdrobustによるパラメトリックRDDの「模倣」
rdrobustをパラメトリックな手法のように動作させるには、以下の2つの設定が鍵となります。
- バンド幅 (
h) を非常に大きくする: 全てのデータが分析に含まれるように、データの範囲全体をカバーするバンド幅を手動で指定します。 - カーネル (
kernel) を一様 (uniform) にする: バンド幅内の全てのデータ点に同じ重みを与えるように設定します。これは、重み付けを行わない標準的な最小二乗法(OLS)と同じです。
# --- rdrobustによるパラメトリックRDDの模倣 ---
# 1. バンド幅をデータ全体をカバーするほど大きく設定
h_global <- max(abs(x - c)) + 0.1 # データ範囲より少しだけ大きくする
# 2. rdrobustを実行。p=1, h=h_global, kernel="uniform" を指定
fit_mimic <- rdrobust(
y = y, x = x, c = c,
p = 1, # 次数1 (線形)
h = h_global, # グローバルなバンド幅
kernel = "uniform"
) # 均等な重み付け
# 結果から「Conventional」な推定値を取得
# (バイアス補正や頑健な標準誤差を使わない、OLSに最も近い推定値)
mimic_effect <- fit_mimic$coef["Conventional", ]
cat("--- 1. rdrobustによるパラメトリック模倣の結果 ---\n")
print(summary(fit_mimic))
cat("\n推定された因果効果 (Conventional):", mimic_effect, "\n\n")--- 1. rdrobustによるパラメトリック模倣の結果 ---
Sharp RD estimates using local polynomial regression.
Number of Obs. 1000
BW type Manual
Kernel Uniform
VCE method NN
Number of Obs. 484 516
Eff. Number of Obs. 484 516
Order est. (p) 1 1
Order bias (q) 2 2
BW est. (h) 1.099 1.099
BW bias (b) 1.099 1.099
rho (h/b) 1.000 1.000
Unique Obs. 484 516
=====================================================================
Point Robust Inference
Estimate z P>|z| [ 95% C.I. ]
---------------------------------------------------------------------
RD Effect 5.075 25.374 0.000 [4.761 , 5.558]
=====================================================================
NULL
推定された因果効果 (Conventional): 5.074793 ステップ3: lmによるパラメトリックRDDの実行
次に、標準的なパラメトリックRDDのモデルをlm()関数で推定します。これは、処置ダミー D と、割り当て変数 x、そしてその交互作用項を含んだモデルです。
モデル式: y = β₀ + τ*D + β₁*x + δ*(x*D) + ε
このモデルにおいて、処置ダミー D の係数 τ が、カットオフ点での因果効果(ジャンプの大きさ)を示します。
# --- lm()によるパラメトリックRDD ---
# 交互作用項を含んだ線形モデルを推定
# xをcで中心化(x-c)するのが丁寧ですが、c=0なのでxのままで同じです
fit_lm <- lm(y ~ D + x + D:x)
# 結果からDの係数を取得
lm_effect <- coef(summary(fit_lm))["D", "Estimate"]
cat("--- 2. lm()によるパラメトリックRDDの結果 ---\n")
print(summary(fit_lm))
cat("\n推定された因果効果 (Dの係数):", lm_effect, "\n\n")--- 2. lm()によるパラメトリックRDDの結果 ---
Call:
lm(formula = y ~ D + x + D:x)
Residuals:
Min 1Q Median 3Q Max
-2.8762 -0.6841 0.0539 0.7131 3.3158
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 0.88348 0.09308 9.492 <2e-16 ***
D 5.07479 0.12737 39.843 <2e-16 ***
x 1.74172 0.16390 10.626 <2e-16 ***
D:x 0.16582 0.22447 0.739 0.46
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 1.005 on 996 degrees of freedom
Multiple R-squared: 0.9229, Adjusted R-squared: 0.9227
F-statistic: 3974 on 3 and 996 DF, p-value: < 2.2e-16
推定された因果効果 (Dの係数): 5.074793 ステップ4: 結果の比較と結論
両方の手法で得られた因果効果を比較しますと、rdrobustのConventionalな推定値と、lm()の処置ダミーDの係数が、いずれも 5.074793 と一致しました。
これは、以下の理由によります。
-
rdrobust(..., h = (データ全体をカバーする幅), kernel = "uniform")の操作は、「カットオフの左右で、全てのデータに均等な重みを与えて、それぞれ線形回帰を行う」ことを意味します。 -
lm(y ~ D + x + D:x)は、「カットオフの左右で、異なる切片と異なる傾きを持つ2つの直線を、全データを使って同時に推定する」モデルです。
これら2つの操作は等価です。rdrobustのノンパラメトリックな枠組みから、その柔軟性を担う「局所性(バンド幅)」と「重み付け(カーネル)」を取り除くことで、結果的にグローバルなパラメトリックモデルであるlmと同じ計算を行っているのです。
以上です。