Rで ボックス・ジェンキンス法 を試みます。
ボックス・ジェンキンス法とは
ボックス・ジェンキンス法とは、統計学者のジョージ・ボックスとグウィリム・ジェンキンスによって提唱された、時系列データを分析し、将来の値を予測するための体系的な手法です。この手法は、過去のデータパターンそのものからモデルを構築することに主眼を置き、特にARIMA(AutoRegressive Integrated Moving Average、自己回帰和分移動平均)モデルを構築する際の一連のプロセスを指します。
この手法は、以下の反復的な4つのステップで構成されます。
- モデルの識別(Identification)
- まず、分析対象の時系列データが定常性(時間の経過によらず平均や分散が一定である性質)を持つかを確認します。
- データのプロット、自己相関関数(ACF)、偏自己相関関数(PACF)のコレログラムを見て、データの特性を把握します。
- データが非定常(トレンドや季節性を持つなど)である場合は、差分を取るなどの処理を施して定常化します。
- 定常化されたデータのACFとPACFのパターンから、構築すべきARIMAモデルの次数(
p,d,q)に見当をつけます。-
p: 自己回帰(AR)の次数 -
d: 差分(I)の階数 -
q: 移動平均(MA)の次数
-
- パラメータの推定(Estimation)
- 識別ステップで特定したARIMA(
p,d,q)モデルのパラメータ(係数)を、実際のデータを用いて統計的に推定します(最尤法などが用いられます)。
- 識別ステップで特定したARIMA(
- モデルの診断(Diagnostic Checking)
- 推定したモデルがデータにうまく適合しているか、仮定が満たされているかを検証します。
- 特に、モデルから得られる残差(実際の値と予測値の差)が、自己相関のないランダムなノイズ(ホワイトノイズ)になっているかを確認します。残差に何らかのパターンが残っている場合、モデルがデータの情報を十分に捉えきれていないことを意味します。
- もしモデルが不適切と判断された場合は、ステップ1に戻り、別の次数のモデルを検討します。
- 予測(Forecasting)
- 診断ステップをクリアしたモデルを用いて、将来の時系列データを予測します。
このように、モデルを「識別」→「推定」→「診断」というサイクルを繰り返して最適なモデルを見つけ出すアプローチが、ボックス・ジェンキンス法の特徴です。
シミュレーション
ここでは、あらかじめARIMA(1, 1, 1)の構造を持つサンプルデータを作成し、このデータを分析することで、ボックス・ジェンキンス法の手順に沿って、元の正しいモデル構造を突き止められるか試してみます。
なお、有意水準は5%とします。
サンプルデータは以下の構造とします。
-
order = c(1, 1, 1): ARIMAモデルの次数(p, d, q)は(1, 1, 1)。 -
ar = 0.7: AR(1)モデルの係数 (\(\phi_1\)) は0.7。 -
ma = 0.7: MA(1)モデルの係数 (\(\theta_1\)) は0.7。
時系列データを \(Y_t\)、時刻 \(t\) におけるホワイトノイズを \(\varepsilon_t\) とします。
このモデルは、 \(Y_t\) の1階差分系列 \(W_t = Y_t - Y_{t-1}\) が、定常な ARMA(1, 1)モデルに従うことを意味しますので、以下のように表されます。
\[
W_t = 0.7 W_{t-1} + \varepsilon_t + 0.7 \varepsilon_{t-1}
\]
この式に \(W_t = Y_t - Y_{t-1}\) を代入すると、
\[
(Y_t - Y_{t-1}) = 0.7 (Y_{t-1} - Y_{t-2}) + \varepsilon_t + 0.7 \varepsilon_{t-1}
\]
また、後退オペレータ \(B\) (\(B Y_t = Y_{t-1}\))を使うと、ARIMA(p, d, q)モデルの一般式は、
\[
(1 - \sum_{i=1}^{p} \phi_i B^i) (1-B)^d Y_t = (1 + \sum_{j=1}^{q} \theta_j B^j) \varepsilon_t
\]
ですので、パラメータ p=1, d=1, q=1, \(\phi_1=0.7\), \(\theta_1=0.7\) から、モデルは、
\[
(1 - 0.7 B) (1 - B) Y_t = (1 + 0.7 B) \varepsilon_t
\] と表すことができます。
ステップ0: サンプルデータの作成
ARIMA(p=1, d=1, q=1)モデルに従う時系列データを作成します。
# 必要なライブラリを読み込みます
library(forecast)
library(tseries)
library(ggplot2)
# 再現性のために乱数のシードを固定します
seed <- 20250927
set.seed(seed)
# ARIMA(1, 1, 1)モデルからサンプルデータを200個生成
# ar = 0.7: AR項の係数, ma = 0.7: MA項の係数
sim_data <- arima.sim(
n = 200,
model = list(order = c(1, 1, 1), ar = 0.7, ma = 0.7),
sd = 1.5 # ノイズの標準偏差
)
# 元の時系列データをプロットして確認
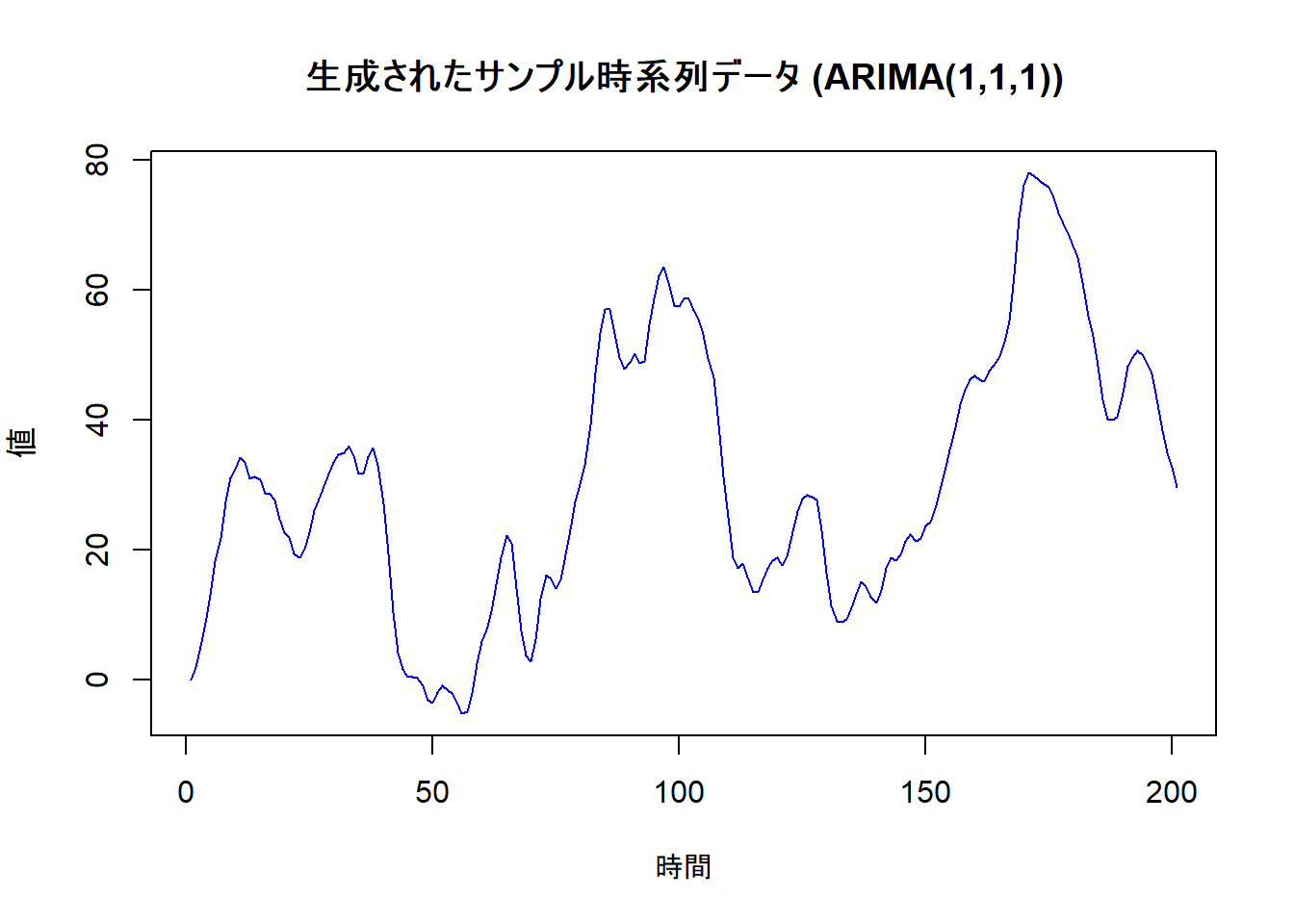
plot(sim_data,
main = "生成されたサンプル時系列データ (ARIMA(1,1,1))",
xlab = "時間",
ylab = "値",
col = "blue"
)ステップ1: モデルの識別
データが定常であるか否かを、コレログラムと統計検定で確認します。
(1-1) 元データのACFとPACFを確認
# ACFとPACFを並べてプロット
par(mfrow = c(1, 2))
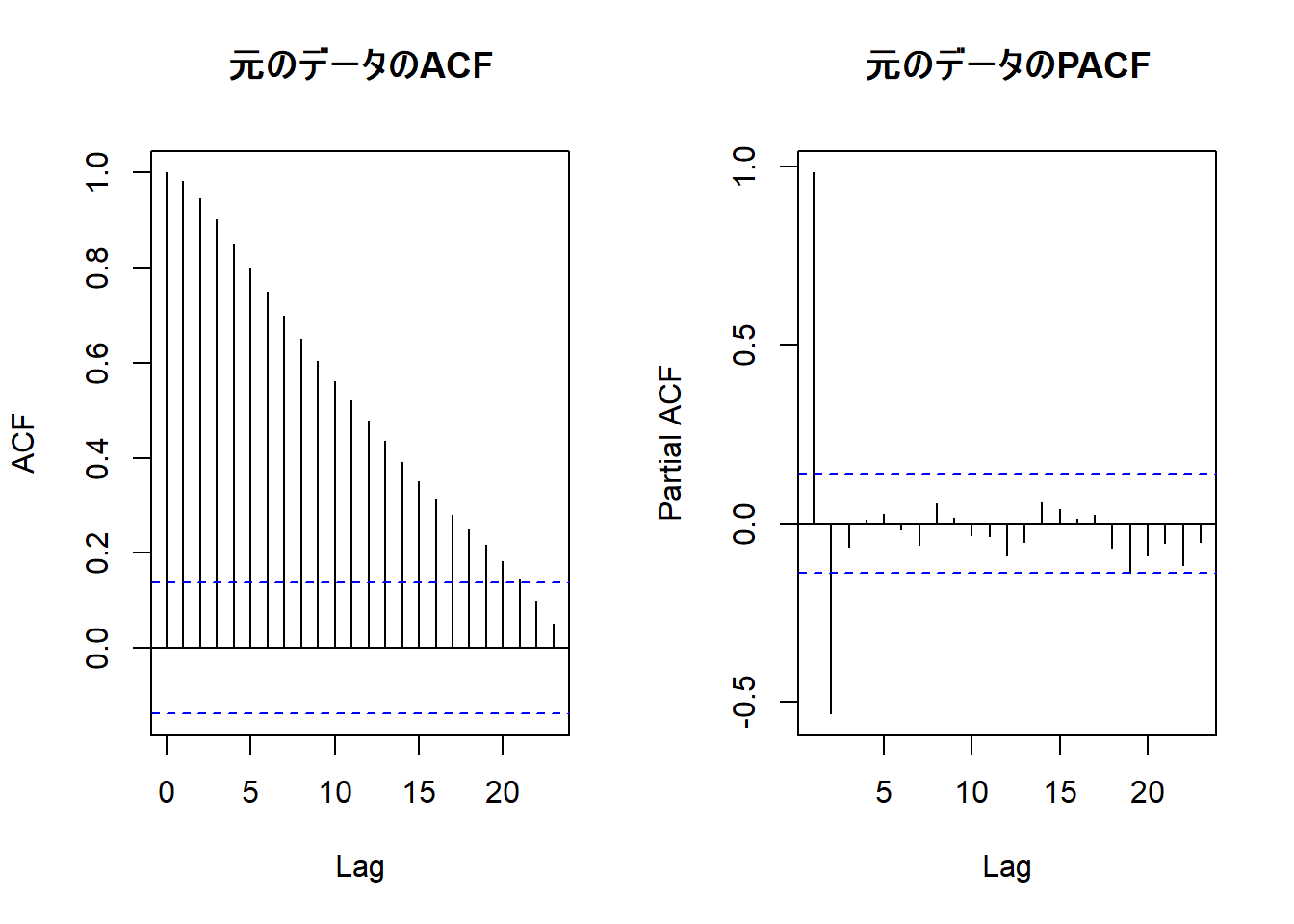
acf(sim_data, main = "元のデータのACF")
pacf(sim_data, main = "元のデータのPACF")ACF(自己相関)がなかなか減衰しないのは、非定常系列の典型的な特徴です。
(1-2) 単位根検定(ADF検定)による定常性の確認
# 帰無仮説 H0: データは単位根を持つ(非定常である)
adf_test_result <- adf.test(sim_data)
cat("\nADF検定の結果:\n")
print(adf_test_result)
ADF検定の結果:
Augmented Dickey-Fuller Test
data: sim_data
Dickey-Fuller = -3.1106, Lag order = 5, p-value = 0.1109
alternative hypothesis: stationaryp値が有意水準5%より大きいため、帰無仮説 H0: データは単位根を持つ を棄却できません。
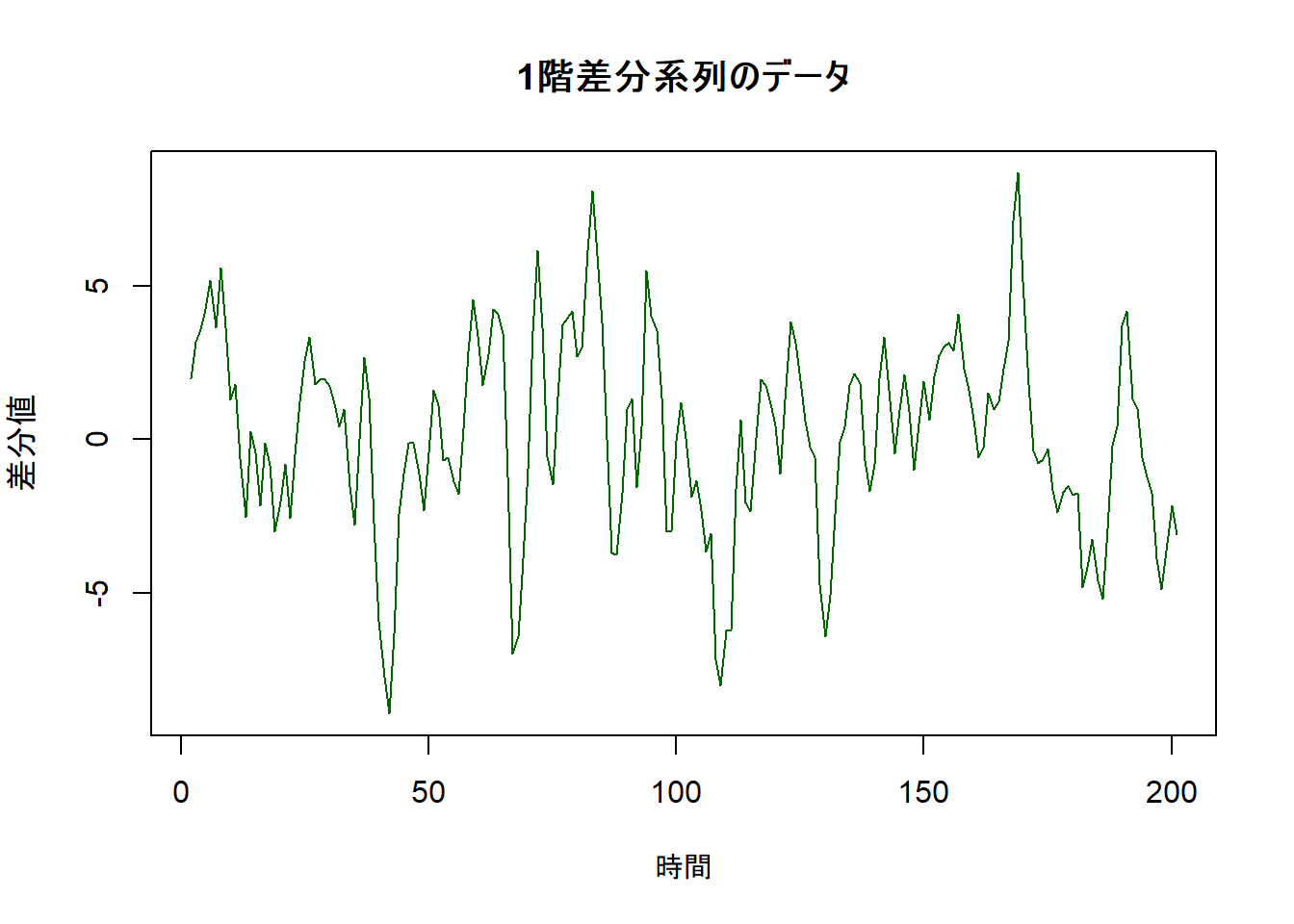
(1-3) 差分を取って定常化
データを定常化するために、1階差分を取ります。
(1-4) 差分系列の定常性を再度確認
差分系列が定常になったか、再度ACF/PACFとADF検定で確認します。

# 差分系列のACFとPACF
par(mfrow = c(1, 2))
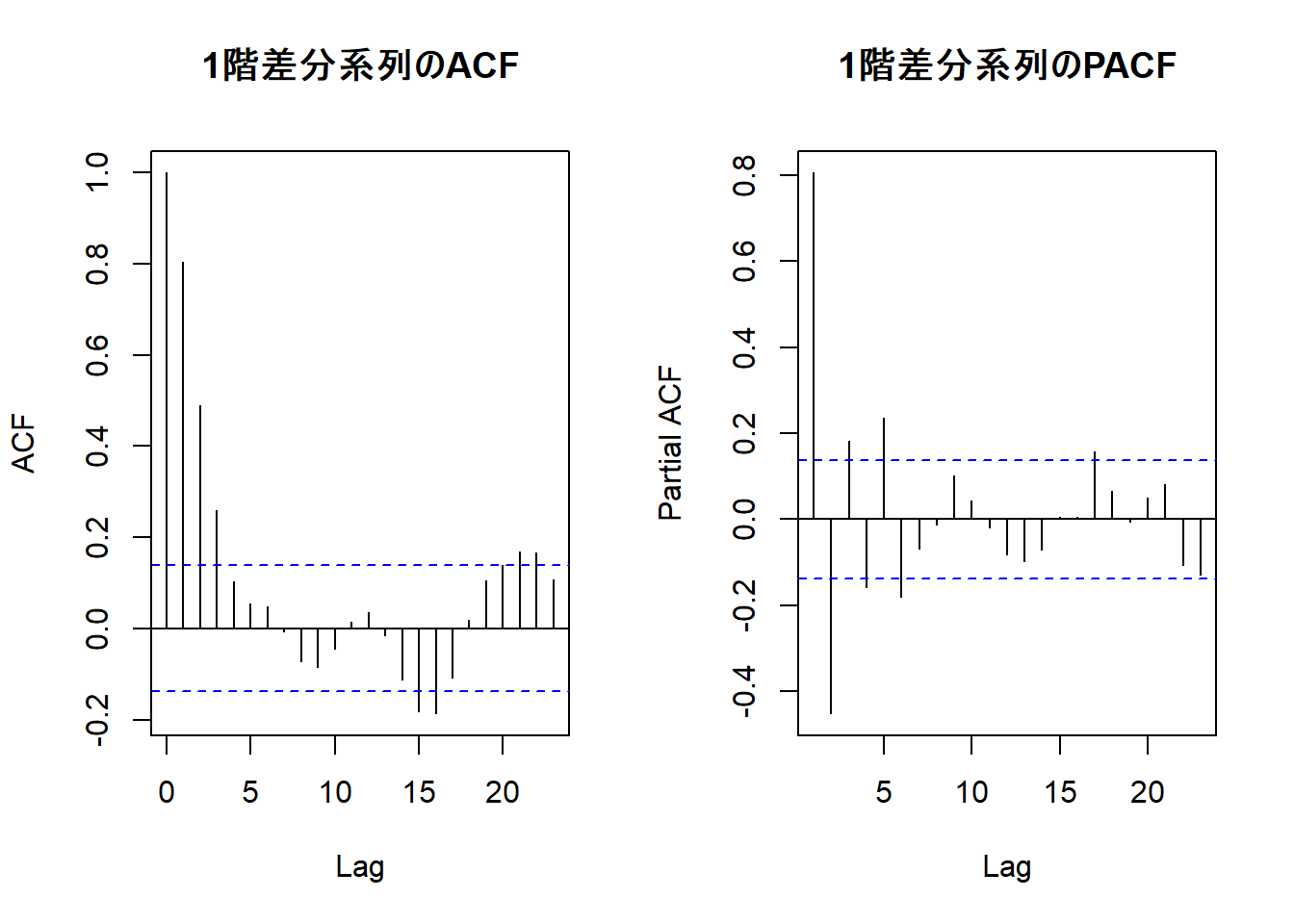
acf(diff_data, main = "1階差分系列のACF")
pacf(diff_data, main = "1階差分系列のPACF")
# 差分系列でADF検定
adf_test_diff_result <- adf.test(diff_data)
cat("差分系列のADF検定の結果:\n")
print(adf_test_diff_result)差分系列のADF検定の結果:
Augmented Dickey-Fuller Test
data: diff_data
Dickey-Fuller = -4.7457, Lag order = 5, p-value = 0.01
alternative hypothesis: stationary| モデル | ACFの形状 | PACFの形状 |
|---|---|---|
| AR(p)モデル | テーリング・オフ (指数的に減衰するか、振動しながら減衰する) | カットオフ (ラグ p までは有意な値を持ち、ラグ p+1 以降は急に0に近づく) |
| MA(q)モデル | カットオフ (ラグ q までは有意な値を持ち、ラグ q+1 以降は急に0に近づく) | テーリング・オフ (指数的に減衰するか、振動しながら減衰する) |
| ARMA(p, q)モデル | テーリング・オフ (ラグ q 以降、AR(p)的な減衰が始まる) | テーリング・オフ (ラグ p 以降、MA(q)的な減衰が始まる) |
- カットオフ (Cut off):あるラグを境に、相関が急に有意でなくなる状態を指します。
- テーリング・オフ (Tailing off):相関がゆっくりと時間をかけて減衰していく状態を指します。
- 1階差分系列の単位根検定の結果は、p値が有意水準を下回っていますので、帰無仮説 H0: データは単位根を持つ は棄却され、モデルは ARIMA(p, 1, q) と考えられます。
- ACFにはラグ1以降に自己相関が徐々に減衰していくパターンが見られます。
- PACFを確認しますと、ラグ2以降でカットオフされる原系列の場合と異なり、振動しながらの減衰が見られます。
- 上記の2、3から、ARMA(1,1)モデルが示唆されていると本ポストでは判断します。
ステップ2: パラメータの推定
識別した ARIMA(1, 1, 1) モデルをデータに当てはめ、パラメータを推定します。
# Arima関数でモデルを推定
model_fit <- Arima(sim_data, order = c(1, 1, 1))
# 結果の表示
print(summary(model_fit))Series: sim_data
ARIMA(1,1,1)
Coefficients:
ar1 ma1
0.6242 0.7760
s.e. 0.0584 0.0487
sigma^2 = 2.354: log likelihood = -369.48
AIC=744.95 AICc=745.08 BIC=754.85
Training set error measures:
ME RMSE MAE MPE MAPE MASE ACF1
Training set 0.02059956 1.522633 1.1875 1.489874 10.25888 0.4794078 0.00404797推定された係数は ar1 = 0.6242, ma1 = 0.7760 であり、それぞれの s.e は 0.0584 と 0.0487 ですので、データを生成した際の真のパラメータ (ar = 0.7, ma = 0.7) に近い値が推定されました。
ステップ3: モデルの診断
推定したモデルが適切かどうか、残差をチェックして診断します。残差が自己相関のない「ホワイトノイズ」になっていれば、モデルは適切と判断できます。
# checkresiduals関数で残差をまとめて診断
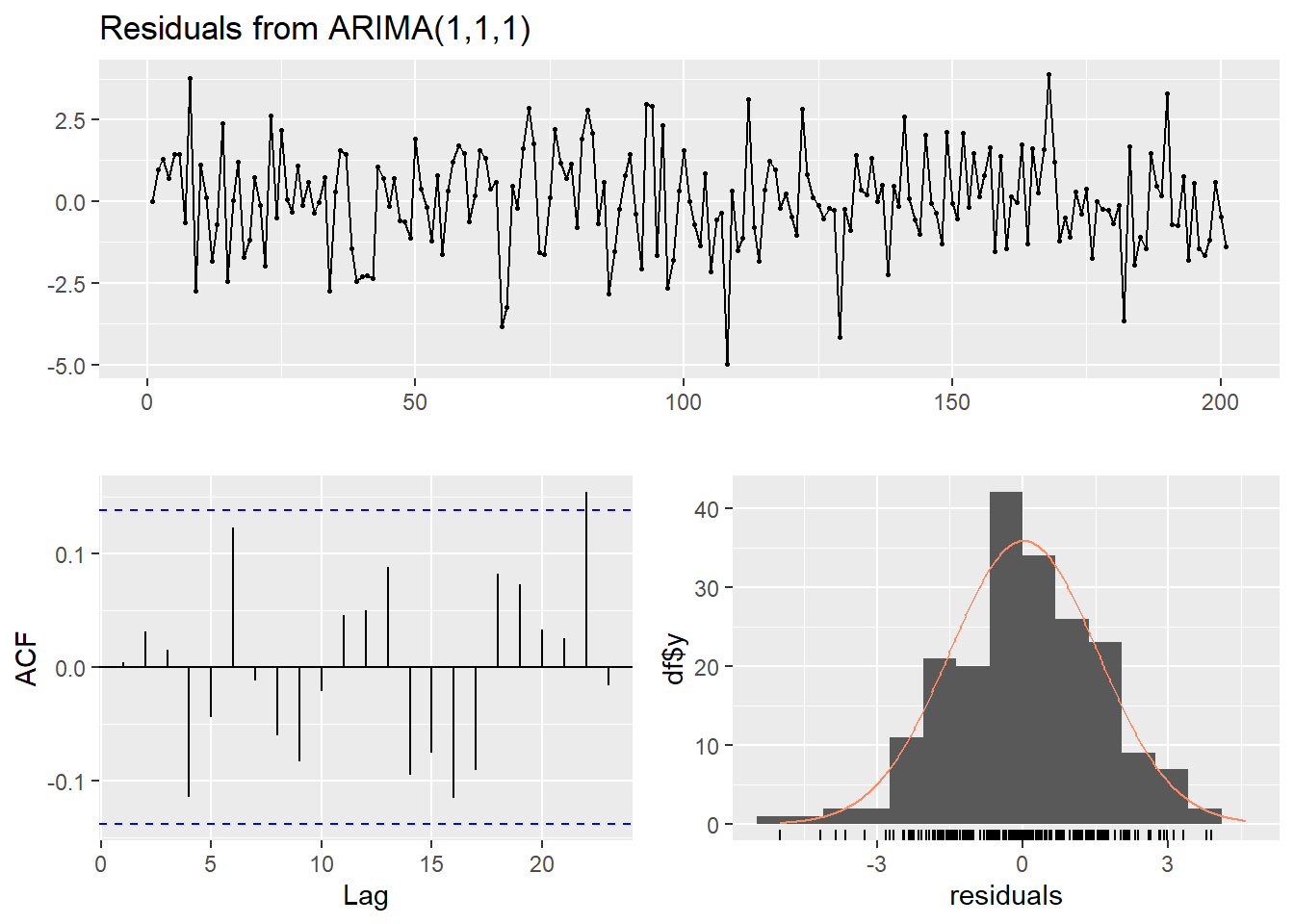
checkresiduals(model_fit)
Ljung-Box test
data: Residuals from ARIMA(1,1,1)
Q* = 8.8839, df = 8, p-value = 0.3522
Model df: 2. Total lags used: 10診断プロットの結果
- 上段の残差プロット: 特定のパターンは見られず、ランダムに変動しています。
- 左下のACFプロット: ラグ22まで有意水準(青い点線)を超えるラグは見られず、自己相関はほぼ解消されています。
- Ljung-Box検定: p値が 0.3522 ですので、H0:残差に自己相関はない とする帰無仮説は棄却されません。
- 以上のことから、残差は ホワイトノイズ であると判断します。
(補足) auto.arimaによる自動モデル選択
ボックス・ジェンキンス法の一連のプロセスを自動で行う auto.arima() の結果と比較してみます。
auto_model <- auto.arima(sim_data, trace = TRUE)
Fitting models using approximations to speed things up...
ARIMA(2,1,2) with drift : 746.4575
ARIMA(0,1,0) with drift : 1026.18
ARIMA(1,1,0) with drift : 817.0257
ARIMA(0,1,1) with drift : 826.0536
ARIMA(0,1,0) : 1024.587
ARIMA(1,1,2) with drift : 745.3578
ARIMA(0,1,2) with drift : 766.8893
ARIMA(1,1,1) with drift : 743.2637
ARIMA(2,1,1) with drift : 748.8098
ARIMA(2,1,0) with drift : 772.4386
ARIMA(1,1,1) : 741.2124
ARIMA(0,1,1) : 824.669
ARIMA(1,1,0) : 814.9662
ARIMA(2,1,1) : 746.7698
ARIMA(1,1,2) : 743.2831
ARIMA(0,1,2) : 765.2224
ARIMA(2,1,0) : 770.3894
ARIMA(2,1,2) : 744.3374
Now re-fitting the best model(s) without approximations...
ARIMA(1,1,1) : 745.0773
Best model: ARIMA(1,1,1) auto.arima()が最終的に選択したモデルは、設定したモデルでもある ARIMA(1,1,1) となりました。
ステップ4: 予測
最後に、構築したモデルを使って将来10期間分の値を予測します。
# forecast関数で将来予測
future_forecast <- forecast(model_fit, h = 10, level = c(80, 95))
# 予測結果をプロット
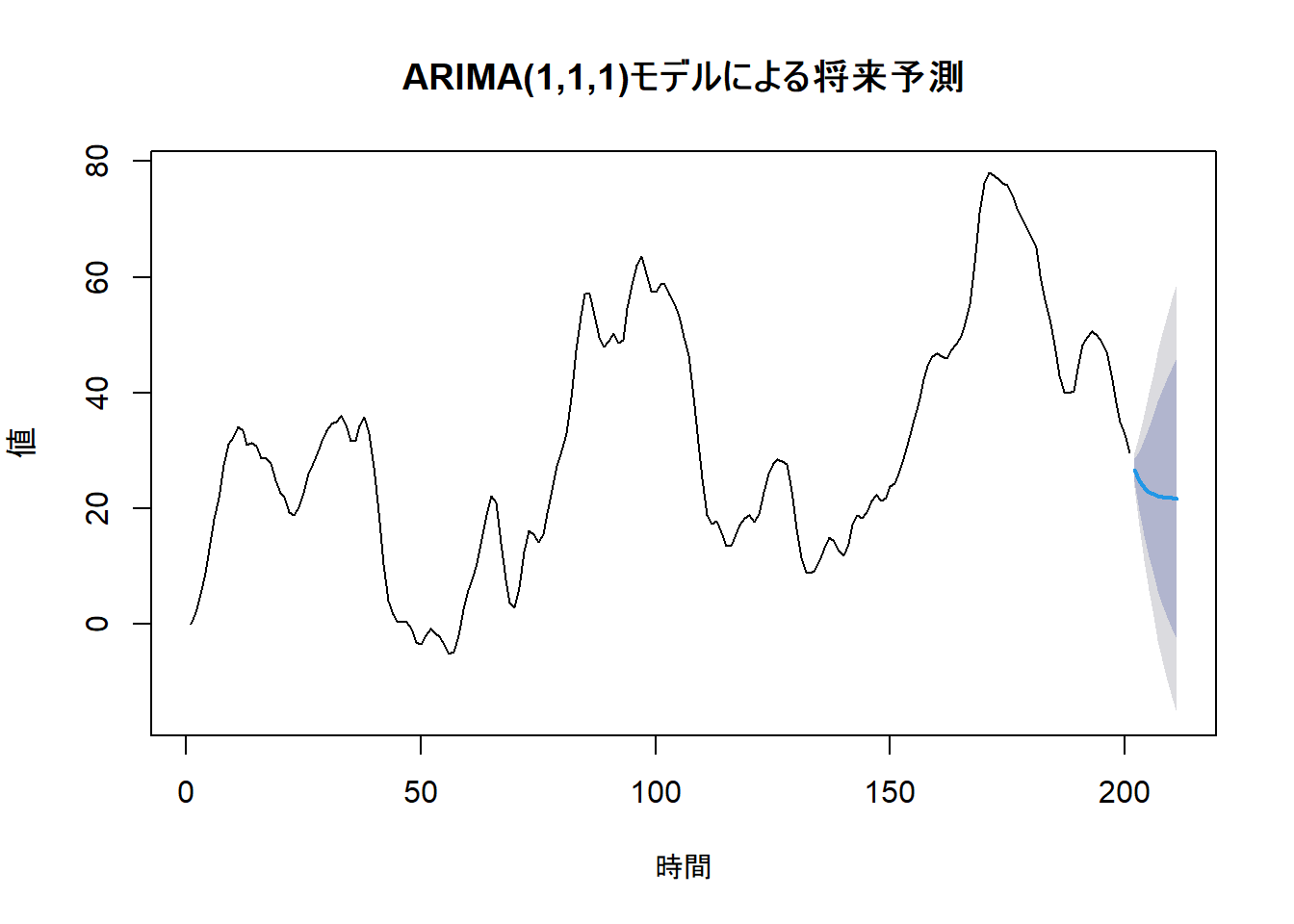
plot(future_forecast,
main = "ARIMA(1,1,1)モデルによる将来予測",
xlab = "時間",
ylab = "値"
)青い線が予測値、色のついた領域が80%(濃い灰色)および95%(薄い灰色)予測区間を示しています。
以上です。