Rの関数:HoltWinters {stats}

はじめに：HoltWinters関数について

Rのstatsパッケージに含まれるHoltWinters関数は、Holt-Winters法（指数平滑化法の一種）を用いて時系列データの平滑化と予測を行うための関数です。

Holt-Winters法は、時系列データが持つ3つの主要な要素をモデル化します。

1. レベル (Level): データの中心的な値。時点\(t\)における時系列の平均的な水準。
2. トレンド (Trend): データの長期的な増加または減少の傾向。時点\(t\)における時系列の傾き。
3. 季節性 (Seasonality): 年、四半期、月、週など、特定の周期で繰り返されるパターン。

この手法は、これらの要素を指数的に重み付けされた過去の観測値を用いて更新していくことで、時系列の動的な変化を捉えます。特に、季節性を持つ時系列データの分析と予測に有用です。

HoltWinters関数は、季節性の変動がレベルの大きさによらず一定であると仮定する加法（additive）モデルと、季節性の変動がレベルの大きさに比例すると仮定する乗法（multiplicative）モデルの両方に対応しています。

モデルの適合度は、3つの平滑化パラメータ alpha（レベル用）、beta（トレンド用）、gamma（季節性用）を調整することで最適化されます。これらのパラメータが指定されない場合、HoltWinters関数は予測誤差の二乗和（Sum of Squared Errors: SSE）を最小化するように最適な値を自動的に推定します。

HoltWinters関数の引数

HoltWinters関数の引数について、以下で説明します。

args(HoltWinters)

function (x, alpha = NULL, beta = NULL, gamma = NULL, seasonal = c("additive", 
    "multiplicative"), start.periods = 2, l.start = NULL, b.start = NULL, 
    s.start = NULL, optim.start = c(alpha = 0.3, beta = 0.1, 
        gamma = 0.1), optim.control = list()) 
NULL

• x
  • 分析対象となる時系列データです。tsクラスのオブジェクトである必要があります。tsオブジェクトは、データベクトルに加えて、開始時期や周期（frequency）などの時間情報を持ちます。
• alpha
  • レベルの平滑化パラメータです。0から1までの値を指定します。この値は、現在のレベルを更新する際に、現在の観測値にどれだけの重みを与えるかを決定します。
  • alphaが1に近いほど、直近の観測値がレベルの更新に強く影響し、ノイズの多いデータに敏感に反応します。
  • alphaが0に近いほど、過去のレベルが強く維持され、平滑化の効果が強くなります。
  • NULL（デフォルト）の場合、関数が予測誤差を最小化する最適なalphaを推定します。
• beta
  • トレンドの平滑化パラメータです。0から1までの値を指定します。この値は、現在のトレンド（傾き）を更新する際に、現在のレベルの変化にどれだけの重みを与えるかを決定します。
  • betaが1に近いほど、直近のレベルの変化がトレンドの更新に強く影響し、トレンドの変化に素早く追従します。
  • betaが0に近いほど、過去のトレンドが強く維持され、トレンドは滑らかに変化します。
  • NULL（デフォルト）の場合、最適なbetaが推定されます。
  • トレンドが存在しないモデル（単純指数平滑化）を当てはめる場合は、beta = FALSEと設定します。
• gamma
  • 季節性の平滑化パラメータです。0から1までの値を指定します。この値は、現在の季節パターンを更新する際に、現在の観測値から推定される季節要素にどれだけの重みを与えるかを決定します。
  • gammaが1に近いほど、直近のデータから推定される季節パターンが強く反映され、季節性の変化に素早く適応します。
  • gammaが0に近いほど、過去の季節パターンが強く維持されます。
  • NULL（デフォルト）の場合、最適なgammaが推定されます。
  • 季節性が存在しないモデル（Holt法）を当てはめる場合は、gamma = FALSEと設定します。
• seasonal
  • 季節性モデルの種類を指定します。
  • "additive"（加法モデル）: 季節変動の大きさが時系列のレベルに依存しない場合に使用します。例えば、毎年クリスマスの売上が100万円増加する、といったケースです。xt = Trend + Seasonal + Error
  • "multiplicative"（乗法モデル）: 季節変動の大きさが時系列のレベルに比例して変化する場合に使用します。例えば、売上が増加するにつれて、クリスマスの売上増も10%増、20%増と比率で増加するケースです。xt = Trend * Seasonal * Error
  • デフォルトでは、"additive"が選択されます。
• start.periods
  • モデルの初期値を計算するために使用する、データセットの先頭部分の周期の数を指定します。デフォルトは2です。例えば、月次データ（周期12）の場合、最初の24ヶ月（2周期分）のデータを使って、季節性の初期パターンなどを計算します。安定した初期値を得るためには、少なくとも2周期分のデータが必要です。
• l.start
  • レベルの初期値(\(l_0\))を手動で設定する場合に指定します。NULL（デフォルト）の場合、start.periodsで指定された期間のデータから自動的に計算されます（加法モデルでは最初の周期のデータの平均値が使われます）。
• b.start
  • トレンドの初期値(\(b_0\))を手動で設定する場合に指定します。NULL（デフォルト）の場合、start.periodsで指定された期間のデータから自動的に計算されます（例：最初の2周期の1周期目と2周期目それぞれの平均値の差分から傾きを計算）。
• s.start
  • 季節性の初期値のベクトルを手動で設定する場合に指定します。ベクトルの長さはデータの周期（frequency）と一致する必要があります。NULL（デフォルト）の場合、start.periodsで指定された期間のデータから自動的に計算されます。
• optim.start
  • alpha, beta, gammaの最適化（数値最適化）を行う際の初期値を指定する、名前付きベクトルです。デフォルトは c(alpha = 0.3, beta = 0.1, gamma = 0.1) です。最適化がうまく収束しない場合に、この初期値を変更することで改善することがあります。
• optim.control
  • 最適化を行う関数 optim に渡す、より詳細な制御パラメータのリストです。例えば、最適化のアルゴリズムや最大反復回数などを指定できます。

シミュレーション

以下に、サンプルデータを作成し、HoltWinters関数を使ってモデルを当てはめ、結果を確認するシミュレーションコードを示します。

1. サンプルデータの作成

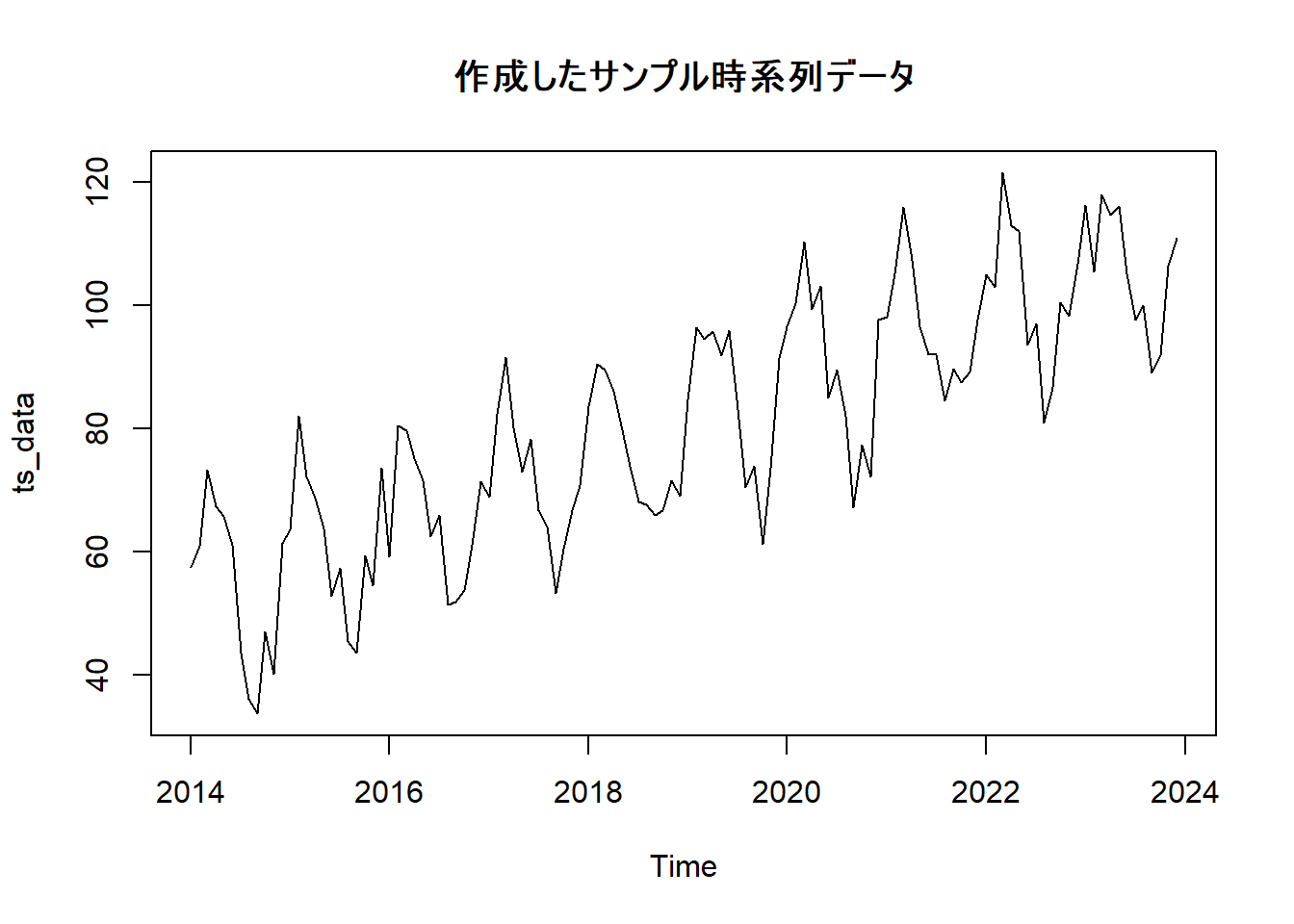
トレンドと周期12の加法的な季節性を持つ月次時系列データを作成します。

# 必要なパッケージの読み込み
library(ggplot2)
library(dplyr)
library(tidyr)
library(lubridate)

# 乱数のシードを固定
seed <- 20250926
set.seed(seed)

# データの設定
n_years <- 10 # 期間（年）
n_obs <- 12 * n_years # データ数 (120)
frequency <- 12 # 周期（月次）
start_year <- 2014 # 開始年

# 時系列の要素を定義
time <- 1:n_obs
intercept <- 50 # 切片（初期レベル）
slope <- 0.5 # 傾き（トレンド）
seasonal_amplitude <- 15 # 季節性の振幅
noise_sd <- 5 # ノイズの標準偏差

# 真のトレンドと季節性を持つデータを生成
# 真のトレンド（データの本来の右上がりの傾向）
true_trend <- intercept + slope * time
# 季節性パターン（sin波で表現）
seasonal_effect <- seasonal_amplitude * sin(2 * pi * time / frequency)
# 観測不可能なノイズ
noise <- rnorm(n_obs, mean = 0, sd = noise_sd)

# 観測データ = 真のトレンド + 季節性 + ノイズ
observed_values <- true_trend + seasonal_effect + noise

# tsオブジェクトに変換
ts_data <- ts(
  observed_values,
  start = c(start_year, 1),
  frequency = frequency
)

plot(ts_data, main = "作成したサンプル時系列データ")

# HoltWintersモデルの適用
# データは加法モデルで作成しましたので、seasonal = "additive" を指定
hw_model <- HoltWinters(ts_data, seasonal = "additive")

cat("--- モデルの推定結果 ---\n")
print(hw_model)

--- モデルの推定結果 ---
Holt-Winters exponential smoothing with trend and additive seasonal component.

Call:
HoltWinters(x = ts_data, seasonal = "additive")

Smoothing parameters:
 alpha: 0.005675687
 beta : 0.005127806
 gamma: 0.414936

Coefficients:
           [,1]
a   107.5239133
b     0.4947676
s1   10.7344739
s2    8.1431846
s3   19.5838431
s4   13.1956845
s5   11.2499120
s6   -0.5035663
s7   -3.8607663
s8   -9.9181537
s9  -14.0897412
s10  -9.8704453
s11  -4.1907957
s12   3.7991388

> HoltWinters(ts_data, seasonal = "multiplicative", beta = FALSE, gamma = FALSE)
Holt-Winters exponential smoothing without trend and without seasonal component.

Call:
HoltWinters(x = ts_data, beta = FALSE, gamma = FALSE, seasonal = "multiplicative")

Smoothing parameters:
 alpha: 0.9274643
 beta : FALSE
 gamma: FALSE

Coefficients:
     [,1]
a 110.517

3. チャートによる確認

観測データ、真のトレンド、モデルによる適合値、そしてモデルが推定したトレンドを重ねてプロットし、視覚的に確認します。

# プロット用のデータフレームを作成
# 時系列の時間情報を抽出
time_index <- time(ts_data)
time_date <- date_decimal(as.numeric(time_index))

# モデルの適合値から各成分を抽出
# fittedは1期先予測値。初期化期間（この場合は12ヶ月）の適合値は計算されない。
fitted_values <- as.numeric(hw_model$fitted[, "xhat"])

# 推定されたトレンド（非季節成分）= レベル + トレンド
estimated_trend <- as.numeric(hw_model$fitted[, "level"] + hw_model$fitted[, "trend"])

# 元データとfittedの長さの差を計算し、その数だけNAを先頭に追加する
n_na <- length(ts_data) - length(fitted_values)

df_plot <- data.frame(
  Date = time_date,
  Observed = as.numeric(ts_data),
  True_Trend = true_trend,
  Fitted = c(rep(NA, n_na), fitted_values),
  Estimated_Trend = c(rep(NA, n_na), estimated_trend)
)

# データを描画しやすいようにロングフォーマットに変換
df_plot_long <- df_plot %>%
  pivot_longer(
    cols = -Date,
    names_to = "Series",
    values_to = "Value"
  ) %>%
  # 日本語の凡例を設定
  mutate(
    Series = factor(Series,
      levels = c("Observed", "Fitted", "True_Trend", "Estimated_Trend"),
      labels = c("観測データ", "モデル適合値", "真のトレンド", "推定されたトレンド")
    )
  )

# ggplotでプロット
g <- ggplot(df_plot_long, aes(x = Date, y = Value, color = Series, linetype = Series)) +
  geom_line(data = ~ subset(.x, Series == "観測データ"), linewidth = 0.8, alpha = 0.7) +
  geom_line(data = ~ subset(.x, Series != "観測データ"), linewidth = 1) +
  scale_color_manual(
    name = "系列",
    values = c("観測データ" = "gray50", "モデル適合値" = "red", "真のトレンド" = "blue", "推定されたトレンド" = "orange")
  ) +
  scale_linetype_manual(
    name = "系列",
    values = c("観測データ" = "solid", "モデル適合値" = "solid", "真のトレンド" = "solid", "推定されたトレンド" = "solid")
  ) +
  labs(
    title = "Holt-Winters法によるトレンドと季節性の推定",
    subtitle = "シミュレーションデータによるモデルの性能評価",
    x = "日付",
    y = "値"
  ) +
  theme_bw() +
  theme(
    legend.position = "bottom"
  )

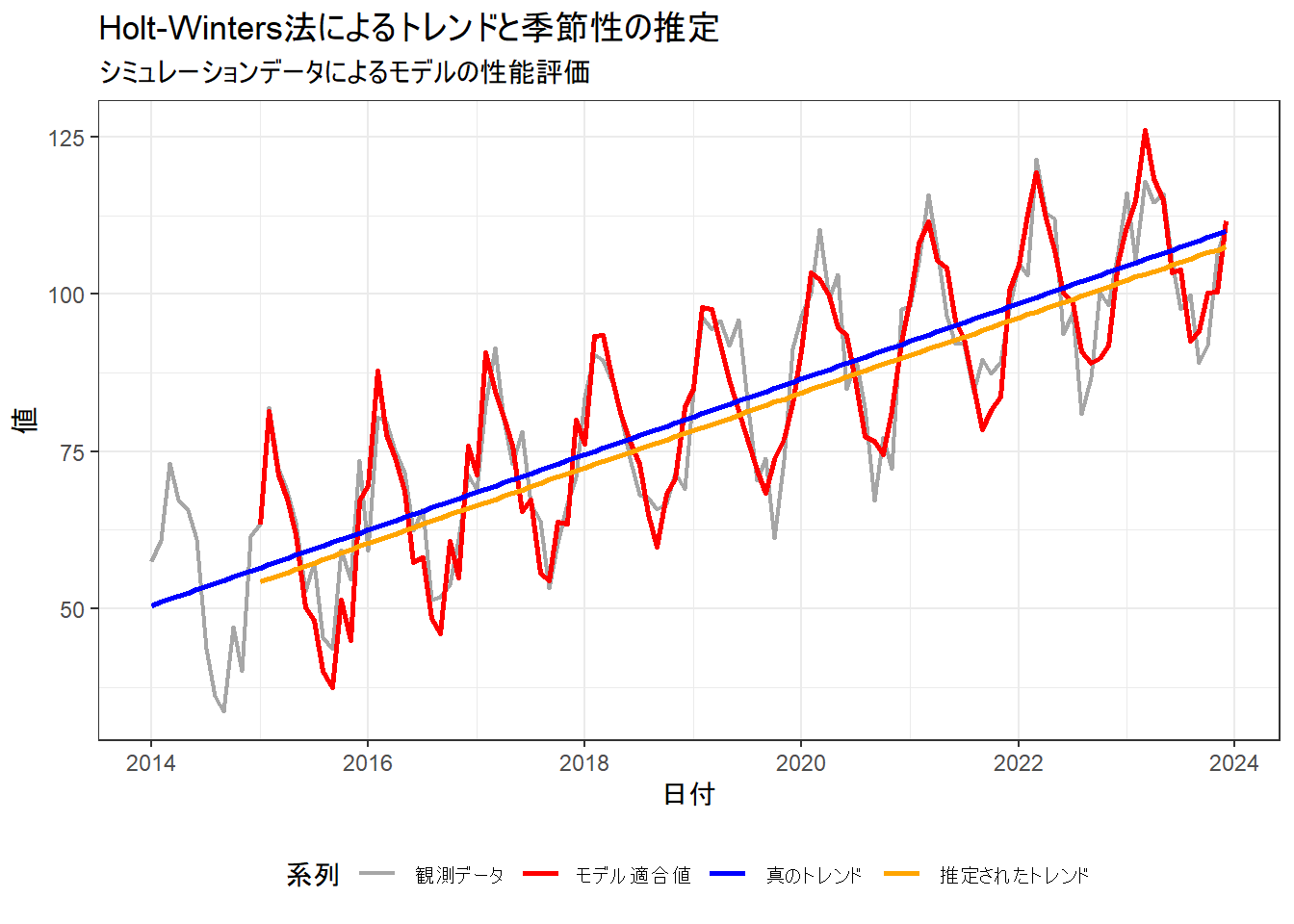
print(g)

Figure 2 から、以下のことが分かります。

1. 「モデル適合値」（赤色線）は「観測データ」（灰色線）の季節性を捉えています。
2. 「推定されたトレンド」（橙色）は、データ生成時に設定した「真のトレンド」（青線）に近い位置で平行に走っています。

以上です。