Rで加重最小二乗法(Weighted Least Squares, WLS)を試みます。
1. 「加重最小二乗法」とは
加重最小二乗法 (Weighted Least Squares, WLS) は、回帰分析の手法の一つです。通常の最小二乗法 (Ordinary Least Squares, OLS) を拡張したもので、特に「不均一分散」の問題に対処する場合に用いられます。
通常の最小二乗法 (OLS) とその仮定
OLSは、データ点と回帰直線との距離(残差)の二乗和が最も小さくなるように回帰係数を決定します。このOLSが最良の推定値(最も効率的で偏りのない推定値)を与えるためには、いくつかの仮定を満たす必要があります。その仮定の一つが「誤差の等分散性」です。
- 等分散性 (Homoscedasticity): 誤差のばらつき(分散)が、説明変数の値によらず一定であるという仮定です。
不均一分散の問題
しかし、実際のデータではこの仮定が満たされないことがよくあります。例えば、説明変数の値が大きくなるにつれて、目的変数のばらつきも大きくなるようなケースです。これを「不均一分散 (Heteroscedasticity)」と呼びます。
不均一分散が存在する場合、OLSで回帰分析を行うと以下のような問題が生じます。
- 推定の効率性の低下: 回帰係数の推定値は依然として偏りはありませんが、そのばらつきが大きくなり、「最良」の推定量ではなくなります。
- 標準誤差の誤り: 回帰係数の標準誤差が正しく計算されなくなり、係数が統計的に有意であるかどうかを判断するt検定などの結果が信頼できなくなります。
加重最小二乗法 (WLS) による解決
WLSは、この不均一分散の問題を解決します。その基本的な考え方は、「信頼性の高いデータ点(=ばらつきの小さいデータ点)をより重視する」というものです。
具体的には、各データ点に「重み」を付けて残差の二乗和を計算します。
- ばらつきが小さいデータ点には、大きな重みを与える。
- ばらつきが大きいデータ点には、小さな重みを与える。
一般的に、重みは誤差の分散の逆数(1 / 分散)に比例するように設定されます。これにより、ばらつきの大きいデータが回帰直線に与える影響を相対的に小さくし、より信頼性の高い回帰モデルを構築することができます。
2. シミュレーションのシナリオ:広告費と売上の関係
あるマーケティングアナリストが、企業の「広告宣伝費」が「売上」にどれだけ影響を与えるかを分析しようとしています。彼は様々な規模の企業(中小企業から大企業まで)100社からデータを集めました。
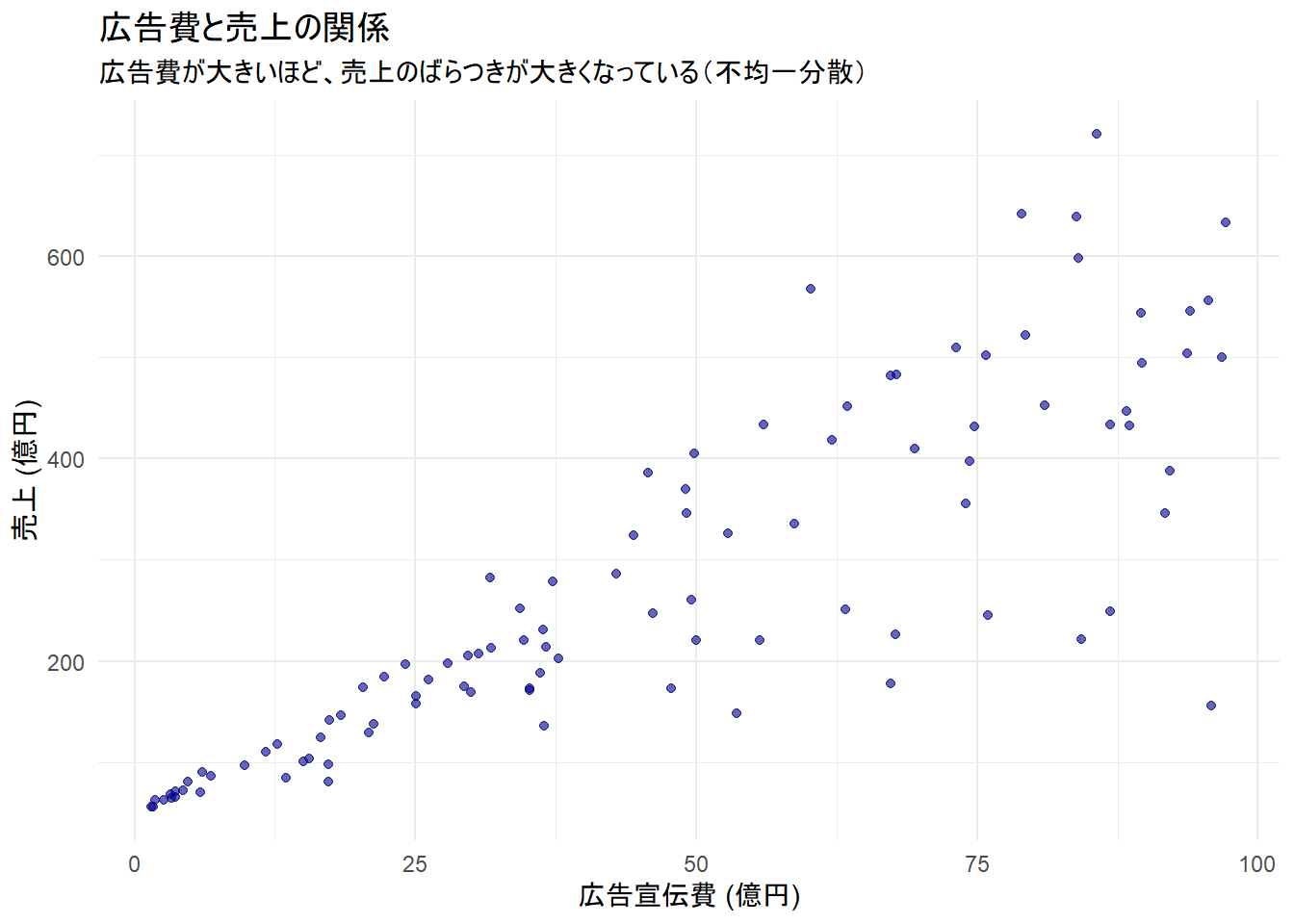
データをプロットしてみると、次のような傾向が見られました。
- 中小企業: 広告宣伝費も売上も比較的小さく、売上の変動幅も小さい。広告の効果が比較的予測しやすい。
- 大企業: 広告宣伝費も売上も非常に大きい。しかし、市場での競争、ブランド力、経済全体の動向など、広告費以外の要因も複雑に絡み合うため、同じくらいの広告費を投じても、売上の結果には大きなばらつきが見られる。
この状況は、まさに「広告宣伝費(説明変数)が大きくなるほど、売上のばらつき(誤差の分散)も大きくなる」という典型的な不均一分散の例です。
このデータに通常の最小二乗法(OLS)を適用すると、ばらつきの大きい大企業のデータにモデルが過剰に引っ張られてしまい、広告費と売上の関係を正しく評価できない可能性があります。
そこで、データのばらつき(信頼性)に応じて重みを変える「加重最小二乗法(WLS)」を用い、より精度の高い分析を行うことにしました。
3. Rによるシミュレーションコード
上記のシナリオに沿って、R言語でシミュレーションを行います。
- 不均一分散を持つ「広告費と売上」のサンプルデータを生成します。
- 生成したデータに対し、OLSとWLSの両方で回帰分析を行います。
- 両者の結果を比較し、WLSの有効性を確認します。
1. シミュレーションデータの生成
広告費と売上の関係について、不均一分散を持つデータを100社分生成します。
# 必要なライブラリを読み込み
library(ggplot2)
library(dplyr)
# 再現性のために乱数のシードを設定
seed <- 20250912
set.seed(seed)
# 企業数
n <- 100
# 真のモデル(私たちが知りたい本当の関係)を設定
# 売上 = 50 + 5 * 広告費 + 誤差
true_intercept <- 50 # 基礎売上(億円)
true_slope <- 5 # 広告費1億円あたりの売上増加分(億円)
# 説明変数 X: 広告宣伝費(億円)
# 中小企業から大企業までを表現するため、1から100の範囲でランダムに生成
ad_cost <- runif(n, min = 1, max = 100)
# 不均一分散の誤差を生成
# 広告費(ad_cost)が大きくなるほど、誤差の標準偏差が大きくなるように設定
error_sd <- 1.5 * ad_cost
error <- rnorm(n, mean = 0, sd = error_sd)
# 目的変数 Y: 売上(億円)
sales <- true_intercept + true_slope * ad_cost + error
# データフレームにまとめる
df <- data.frame(
ad_cost = ad_cost,
sales = sales
)
# 可視化
g_scatter <- ggplot(df, aes(x = ad_cost, y = sales)) +
geom_point(alpha = 0.6, color = "darkblue") +
labs(
title = "広告費と売上の関係",
x = "広告宣伝費 (億円)",
y = "売上 (億円)",
subtitle = "広告費が大きいほど、売上のばらつきが大きくなっている(不均一分散)"
) +
theme_minimal()
print(g_scatter)2. 通常の最小二乗法 (OLS) による分析
# OLSモデルを当てはめる
model_ols <- lm(sales ~ ad_cost, data = df)
cat("--- OLSによる回帰分析の結果 ---\n")
print(summary(model_ols))--- OLSによる回帰分析の結果 ---
Call:
lm(formula = sales ~ ad_cost, data = df)
Residuals:
Min 1Q Median 3Q Max
-355.20 -28.97 1.77 30.59 257.88
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 52.1779 16.8597 3.095 0.00257 **
ad_cost 4.7914 0.3065 15.630 < 2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 91.37 on 98 degrees of freedom
Multiple R-squared: 0.7137, Adjusted R-squared: 0.7108
F-statistic: 244.3 on 1 and 98 DF, p-value: < 2.2e-163. 加重最小二乗法 (WLS) による分析
# WLSのための重みを計算
# 重みは誤差の分散の逆数に比例させる。
# このシミュレーションでは、誤差分散を (1.5 * ad_cost)^2 と設定しましたので、
# 理想的な重みは 1 / ad_cost^2 となります。
# 実務では真の分散が未知のため、OLSの残差などから推定する必要があります。
weights <- 1 / ad_cost^2
# WLSモデルを当てはめる
model_wls <- lm(sales ~ ad_cost, data = df, weights = weights)
cat("--- WLSによる回帰分析の結果 ---\n")
print(summary(model_wls))--- WLSによる回帰分析の結果 ---
Call:
lm(formula = sales ~ ad_cost, data = df, weights = weights)
Weighted Residuals:
Min 1Q Median 3Q Max
-3.712 -1.012 0.141 1.133 3.779
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 50.0964 1.2560 39.88 <2e-16 ***
ad_cost 4.8189 0.1725 27.94 <2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 1.507 on 98 degrees of freedom
Multiple R-squared: 0.8884, Adjusted R-squared: 0.8873
F-statistic: 780.5 on 1 and 98 DF, p-value: < 2.2e-164. 結果の比較
cat("---------------------------------------------------\n")
cat(" 係数の比較\n")
cat("---------------------------------------------------\n")
cat(sprintf(" 切片 (Intercept) 傾き (ad_cost)\n"))
cat(sprintf("真の値 %16.3f %14.3f\n", true_intercept, true_slope))
cat(sprintf("OLS推定値 %16.3f %14.3f\n", coef(model_ols)[1], coef(model_ols)[2]))
cat(sprintf("WLS推定値 %16.3f %14.3f\n", coef(model_wls)[1], coef(model_wls)[2]))
cat("---------------------------------------------------\n")---------------------------------------------------
係数の比較
---------------------------------------------------
切片 (Intercept) 傾き (ad_cost)
真の値 50.000 5.000
OLS推定値 52.178 4.791
WLS推定値 50.096 4.819
---------------------------------------------------WLSの推定値の方が、真の値に近いことがわかります。
cat("---------------------------------------------------\n")
cat(" 傾き(ad_cost)の標準誤差の比較\n")
cat("---------------------------------------------------\n")
cat(sprintf("OLS標準誤差: %.3f\n", summary(model_ols)$coefficients[2, 2]))
cat(sprintf("WLS標準誤差: %.3f\n", summary(model_wls)$coefficients[2, 2]))
cat("---------------------------------------------------\n")---------------------------------------------------
傾き(ad_cost)の標準誤差の比較
---------------------------------------------------
OLS標準誤差: 0.307
WLS標準誤差: 0.172
---------------------------------------------------WLSの方が標準誤差が小さく、より効率的な(精度の高い)推定が行えていることを確認できます。
5. 加重最小二乗法による残差
WLSは、元の回帰モデル:
sales = β_0 + β_1 * ad_cost + error
において、誤差の分散が不均一である問題を解決するために、モデル全体に重みの平方根 (sqrt(weights)) を乗じます。
sales * sqrt(w) = β_0 * sqrt(w) + β_1 * ad_cost * sqrt(w) + error * sqrt(w)
以下で、WLSモデルによる残差を求めます。
なお、WLSの残差は residuals(model_wls, type = "pearson") でも求められますため、結果を比較します。
cat("### 1. 標準的なWLSモデルのピアソン残差\n")
# `lm`のweights引数を使ったモデルからピアソン残差を取得
res_pearson <- residuals(model_wls, type = "pearson")
cat("ピアソン残差の最初の6つ:\n")
print(head(res_pearson))
cat("\n")
cat("### 2. 手動で変換したモデルの『生の残差』\n")
# WLSを手動でOLSに変換する
# 目的変数と説明変数の両方に `sqrt(weights)` を掛ける
sales_w <- df$sales * sqrt(weights)
ad_cost_w <- df$ad_cost * sqrt(weights)
intercept_w <- 1 * sqrt(weights) # 切片項にも掛ける
# 変換後のモデルをOLSで推定する
# モデルに intercept_w を入れているため、切片なし `-1` とする
model_manual_wls <- lm(sales_w ~ intercept_w + ad_cost_w - 1)
# このモデルの「生の残差」を取得する
res_manual <- residuals(model_manual_wls)
cat("手動変換モデルの生の残差の最初の6つ:\n")
print(head(res_manual))
cat("\n")
cat("### 3. 結果の比較\n")
cat("ピアソン残差と手動変換モデルの生の残差は一致するか?\n")
print(all.equal(res_pearson, res_manual))
# 参考:手動モデルの係数が元のWLSモデルの係数と一致することも確認
cat("\n参考: WLSモデルと手動変換モデルの係数の比較\n")
cat("lm(weights=...) の係数:\n")
print(coef(model_wls))
cat("\n手動変換モデルの係数:\n")
# intercept_wの係数が切片、ad_cost_wの係数が傾きに対応
print(coef(model_manual_wls))
cat("\n")### 1. 標準的なWLSモデルのピアソン残差
ピアソン残差の最初の6つ:
1 2 3 4 5 6
2.6731824 -2.9238559 1.0755965 2.1945847 0.4764432 -0.3303282
### 2. 手動で変換したモデルの『生の残差』
手動変換モデルの生の残差の最初の6つ:
1 2 3 4 5 6
2.6731824 -2.9238559 1.0755965 2.1945847 0.4764432 -0.3303282
### 3. 結果の比較
ピアソン残差と手動変換モデルの生の残差は一致するか?
[1] TRUE
参考: WLSモデルと手動変換モデルの係数の比較
lm(weights=...) の係数:
(Intercept) ad_cost
50.096450 4.818907
手動変換モデルの係数:
intercept_w ad_cost_w
50.096450 4.818907 6. 結果の可視化(残差プロット)
# 改めて残差を算出します
df$ols_resid <- residuals(model_ols)
df$ols_fitted <- fitted(model_ols)
df$wls_resid <- residuals(model_wls, type = "pearson")
df$wls_fitted <- fitted(model_wls)
# OLSの残差プロット
g_resid_ols <- ggplot(df, aes(x = ols_fitted, y = ols_resid)) +
geom_point(color = "cyan4") +
geom_hline(yintercept = 0, linetype = "dashed", color = "red") +
labs(
title = "OLSの残差プロット",
x = "予測値",
y = "残差"
) +
theme_minimal()
# WLSの残差プロット
g_resid_wls <- ggplot(df, aes(x = wls_fitted, y = wls_resid)) +
geom_point(color = "orange") +
geom_hline(yintercept = 0, linetype = "dashed", color = "red") +
labs(
title = "WLSの残差プロット",
x = "予測値",
y = "重み付け済み残差"
) +
theme_minimal()
library(patchwork)
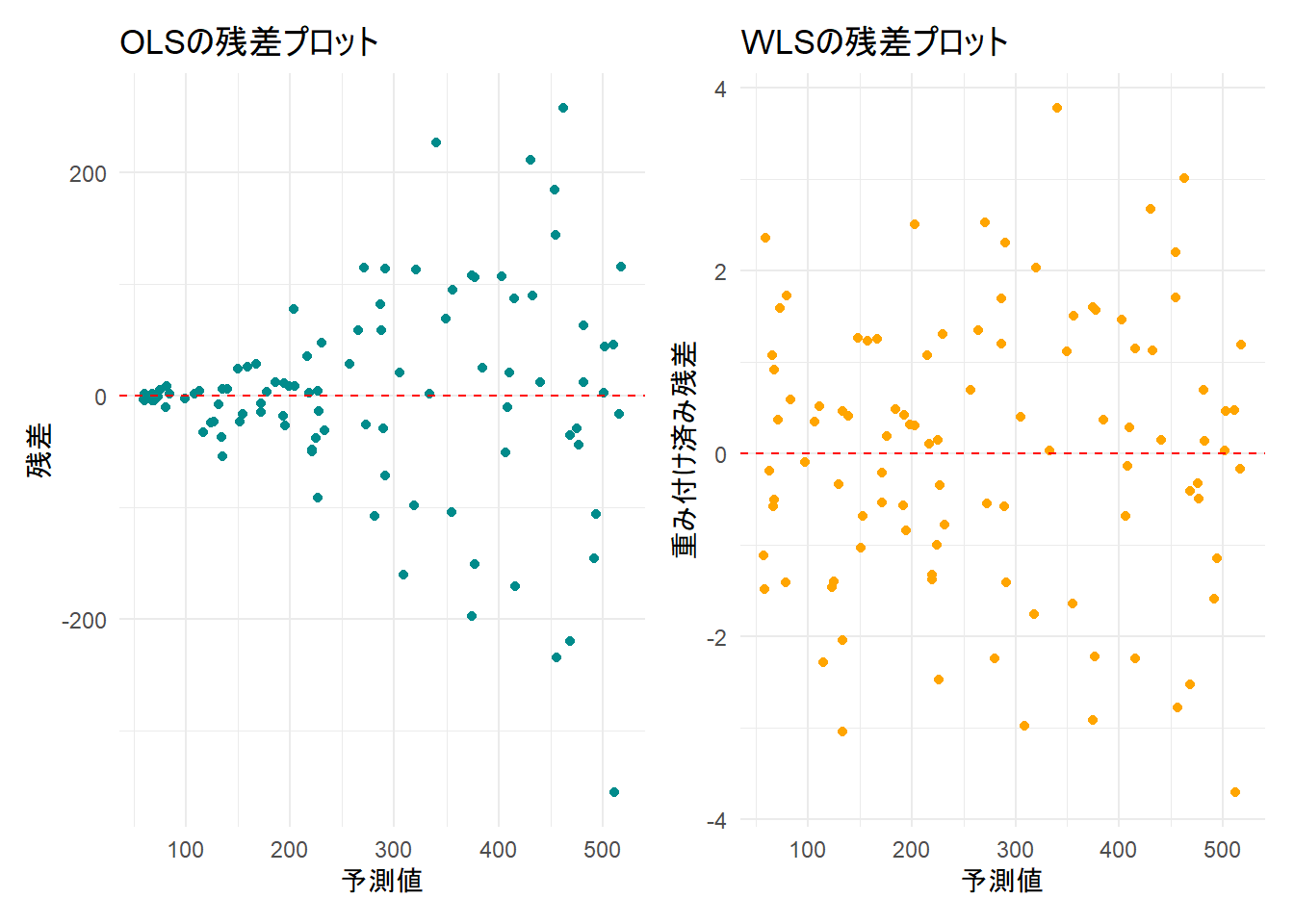
g_resid_ols + g_resid_wlsFigure 2 のOLSの残差プロット(左)では、予測値が大きくなるにつれて残差のばらつきが広がる「メガホン型」になっており、不均一分散の存在が明確です。
一方、WLSの残差プロット(右)では、そのような残差のばらつきの広がりは見られないことを確認できます。
以上です。