Rで 構造方程式モデリング を試みます。
1. 構造方程式モデリング(Structural Equation Modeling: SEM)とは
構造方程式モデリング(以下、SEM)は、複数の変数間の複雑な因果関係を統計的に検証するための分析手法です。特に、アンケート調査などで直接測定することが難しい心理的な概念(例:「幸福度」、「学習意欲」、「ブランドイメージ」など)を扱えるために利用されます。
SEMは、主に2つの要素から構成されます。
- 測定モデル (Measurement Model)
- 潜在変数 (Latent Variable): 直接測定できない、抽象的な概念です(例:仕事の満足度)。
- 観測変数 (Observed Variable): アンケートの質問項目など、直接測定・観察できる具体的なデータです(例:「今の仕事に満足していますか?」という質問への5段階評価の回答)。
- 測定モデルは、「複数の観測変数(具体的な質問)を使って、その背後にある潜在変数(抽象的な概念)をどの程度うまく測定できているか」を検証する部分です。これは因子分析に近い考え方です。
- 構造モデル (Structural Model)
- これは、潜在変数間の因果関係(パス)を検証する部分です。
- 例えば、「『仕事のやりがい』が高いほど、『仕事満足度』も高くなるだろう」といった仮説をモデル化し、データによってその仮説が支持されるかどうかを統計的に検証します。
SEMの利点
- 複雑な因果関係の検証: 「A → B → C」のような媒介効果や、「XとYがともにZに影響する」といった複数の関係を同時に分析できます。
- 測定誤差の考慮: アンケートの回答には必ず誤差が含まれますが、SEMはその誤差を統計的に分離して分析するため、より正確な関係性を捉えることができます。
- 仮説の検証: 研究者が理論に基づいて立てた仮説(モデル)が、実際のデータとどの程度一致しているか(適合度)を評価できます。
つまり、SEMは「抽象的な概念同士の因果関係を、具体的なデータを使って検証するためのツール」です。
2. シミュレーションのためのシナリオ
今回は、多くの人にとって身近な「職場の環境が従業員の満足度に与える影響」というテーマでシミュレーションを行います。
【ストーリー】
ある企業の人事部が、従業員のエンゲージメント向上のために「何が仕事の満足度を高めるのか」を調査することにしました。 これまでの経験から、人事部は「『仕事のやりがい』と『職場の良好な人間関係』が、従業員の『仕事満足度』にプラスの影響を与えるのではないか」という仮説を立てました。
この仮説を検証するために、以下の3つの潜在変数を設定し、それぞれに関連するアンケート調査を実施したとします。
【モデルの構成要素】
- 潜在変数1:仕事のやりがい (やりがい)
- 観測変数 x1: 「現在の仕事内容に興味・関心を持っている」
- 観測変数 x2: 「自分のスキルや能力を仕事で活かせている」
- 観測変数 x3: 「仕事を通じて自己の成長を実感できる」
- 潜在変数2:職場の人間関係 (人間関係)
- 観測変数 x4: 「上司との関係は良好だ」
- 観測変数 x5: 「同僚との関係は良好だ」
- 観測変数 x6: 「チームとしての一体感や協力体制がある」
- 潜在変数3(結果変数):仕事満足度 (満足度)
- 観測変数 y1: 「総合的にみて、現在の仕事に満足している」
- 観測変数 y2: 「今後もこの会社で働き続けたいと思う」
- 観測変数 y3: 「友人や知人に自分の会社を勧めたいと思う」
【検証したい仮説(構造モデル)】
- 仮説1: 「仕事のやりがい」は「仕事満足度」に正の影響を与える。
- 仮説2: 「職場の人間関係」は「仕事満足度」に正の影響を与える。
このシナリオに基づき、300人の従業員から得られたアンケート回答のシミュレーションデータを作成し、SEMで仮説を検証します。
3. Rによるシミュレーションコード
以下に、上記のシナリオに沿ったSEMのシミュレーションを実行するRコードを示します。 このコードは、以下のステップで構成されています。
- 準備: 必要なパッケージを読み込みます。
- データ生成: シナリオに沿った「真のモデル」を仮定し、そのモデルからサンプルデータを生成します。
- モデル定義:
lavaanパッケージの構文を使い、分析したいモデルを記述します。 - モデル推定: 生成したデータを使って、定義したモデルのパラメータを推定します。
- 結果の解釈: 分析結果(パス係数や適合度指標)を表示し、解説します。
- 可視化: 分析結果をパス図として描画します。
# 1. 準備:必要なパッケージの読み込み
# ------------------------------------------------
library(lavaan)
library(MASS)
library(semPlot)
# 2. データ生成:シナリオに基づいたシミュレーションデータの作成
# ------------------------------------------------
# シミュレーションの再現性を確保するために乱数シードを固定
seed <- 20250901
set.seed(seed)
# サンプルサイズを設定
N <- 300
# 潜在変数間の関係(構造モデル)を定義
# やりがい -> 満足度 のパス係数を 0.4
# 人間関係 -> 満足度 のパス係数を 0.5
beta_matrix <- matrix(c(
0.0, 0.0, 0.0,
0.0, 0.0, 0.0,
0.4, 0.5, 0.0
), nrow = 3, byrow = TRUE)
colnames(beta_matrix) <- rownames(beta_matrix) <- c("やりがい", "人間関係", "満足度")
# 潜在変数の(構造モデルで説明されない部分の)共分散行列を定義
# 対角成分は分散、非対角成分は共分散
psi_matrix <- matrix(c(
1.0, 0.3, 0.0, # やりがいと人間関係には少し相関(0.3)があると仮定
0.3, 1.0, 0.0,
0.0, 0.0, 1.0 # 満足度の残差分散は後で計算
), nrow = 3, byrow = TRUE)
colnames(psi_matrix) <- rownames(psi_matrix) <- c("やりがい", "人間関係", "満足度")
# 潜在変数の共分散行列を計算
I <- diag(nrow(beta_matrix))
sigma_eta <- solve(I - beta_matrix) %*% psi_matrix %*% t(solve(I - beta_matrix))
# 満足度の残差分散を調整
# R^2 = 1 - (残差分散 / 全分散) となるように設定
# ここではR^2が約0.5になるように調整
sigma_eta[3, 3] <- 1 - (0.4^2 * sigma_eta[1, 1] + 0.5^2 * sigma_eta[2, 2] + 2 * 0.4 * 0.5 * sigma_eta[1, 2])
# 観測変数と潜在変数の関係(測定モデル)を定義
# 各観測変数への因子負荷量を設定
lambda_matrix <- matrix(c(
# x1, x2, x3 (やりがい)
0.8, 0.0, 0.0,
0.7, 0.0, 0.0,
0.6, 0.0, 0.0,
# x4, x5, x6 (人間関係)
0.0, 0.8, 0.0,
0.0, 0.7, 0.0,
0.0, 0.9, 0.0,
# y1, y2, y3 (満足度)
0.0, 0.0, 0.8,
0.0, 0.0, 0.9,
0.0, 0.0, 0.7
), nrow = 9, byrow = TRUE)
# 測定誤差の分散を定義
theta_vector <- rep(0.3, 9) # 全ての観測変数で誤差分散を0.3と仮定
theta_matrix <- diag(theta_vector)
# 全観測変数の共分散行列を計算
sigma_observed <- lambda_matrix %*% sigma_eta %*% t(lambda_matrix) + theta_matrix
# 計算した共分散行列を持つ多変量正規分布に従うデータを生成
var_names <- c(paste0("x", 1:6), paste0("y", 1:3))
sim_data <- as.data.frame(mvrnorm(n = N, mu = rep(0, 9), Sigma = sigma_observed))
colnames(sim_data) <- var_names
cat("--- シミュレーションデータの一部を確認 ---\n")
print(head(sim_data))--- シミュレーションデータの一部を確認 ---
x1 x2 x3 x4 x5 x6 y1 y2 y3
1 1.2980106 1.9785949 1.6987471 -0.62113961 0.293073803 -1.11515630 0.3757585 0.6212145 -0.1520366
2 1.3920255 0.2032353 0.6219108 1.05870952 0.941297590 1.24575963 0.3256298 0.7530936 0.8744929
3 0.2837263 0.3245040 0.3676462 1.31560768 0.006543706 -0.06772359 0.2745055 0.2704316 1.3484915
4 1.1823239 1.0555362 0.2554547 1.32815840 0.822047236 -0.15793790 -0.1045643 0.1419149 0.1074600
5 1.0684016 0.8314418 1.0641390 1.17634988 1.552145389 0.89267946 0.8137198 1.3515829 -0.1489496
6 -1.0061788 0.1539703 -0.6233924 0.05810882 0.594113870 -0.35932296 0.4063561 -0.6699949 0.8342281# 3. モデル定義:lavaan構文で分析モデルを記述
# ------------------------------------------------
# =~ : 測定モデル(左辺の潜在変数は、右辺の観測変数群によって測定される)
# ~ : 構造モデル(左辺の変数は、右辺の変数群から影響を受ける)
model_syntax <- "
# 測定モデル
YARIGAI =~ x1 + x2 + x3
NINKAN =~ x4 + x5 + x6
MANZOKU =~ y1 + y2 + y3
# 構造モデル
MANZOKU ~ YARIGAI + NINKAN
"
# 4. モデル推定:sem()関数で分析を実行
# ------------------------------------------------
fit <- sem(model_syntax, data = sim_data)
# 5. 結果の解釈:summary()関数で結果を表示
# ------------------------------------------------
cat("--- 構造方程式モデリングの分析結果 ---\n")
summary(fit, fit.measures = TRUE, standardized = TRUE, rsquare = TRUE)--- 構造方程式モデリングの分析結果 ---
lavaan 0.6-19 ended normally after 36 iterations
Estimator ML
Optimization method NLMINB
Number of model parameters 21
Number of observations 300
Model Test User Model:
Test statistic 19.690
Degrees of freedom 24
P-value (Chi-square) 0.714
Model Test Baseline Model:
Test statistic 1346.589
Degrees of freedom 36
P-value 0.000
User Model versus Baseline Model:
Comparative Fit Index (CFI) 1.000
Tucker-Lewis Index (TLI) 1.005
Loglikelihood and Information Criteria:
Loglikelihood user model (H0) -2773.611
Loglikelihood unrestricted model (H1) -2763.766
Akaike (AIC) 5589.222
Bayesian (BIC) 5667.001
Sample-size adjusted Bayesian (SABIC) 5600.402
Root Mean Square Error of Approximation:
RMSEA 0.000
90 Percent confidence interval - lower 0.000
90 Percent confidence interval - upper 0.036
P-value H_0: RMSEA <= 0.050 0.993
P-value H_0: RMSEA >= 0.080 0.000
Standardized Root Mean Square Residual:
SRMR 0.025
Parameter Estimates:
Standard errors Standard
Information Expected
Information saturated (h1) model Structured
Latent Variables:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
YARIGAI =~
x1 1.000 0.753 0.831
x2 0.987 0.067 14.836 0.000 0.744 0.805
x3 0.833 0.063 13.287 0.000 0.628 0.731
NINKAN =~
x4 1.000 0.772 0.807
x5 0.818 0.060 13.720 0.000 0.632 0.745
x6 1.133 0.070 16.267 0.000 0.875 0.862
MANZOKU =~
y1 1.000 0.492 0.667
y2 1.227 0.100 12.270 0.000 0.604 0.749
y3 0.956 0.093 10.295 0.000 0.471 0.616
Regressions:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
MANZOKU ~
YARIGAI 0.401 0.038 10.678 0.000 0.614 0.614
NINKAN 0.466 0.041 11.510 0.000 0.731 0.731
Covariances:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
YARIGAI ~~
NINKAN 0.160 0.041 3.846 0.000 0.274 0.274
Variances:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
.x1 0.255 0.032 7.964 0.000 0.255 0.310
.x2 0.300 0.034 8.685 0.000 0.300 0.351
.x3 0.343 0.034 10.077 0.000 0.343 0.465
.x4 0.318 0.034 9.291 0.000 0.318 0.348
.x5 0.319 0.031 10.310 0.000 0.319 0.444
.x6 0.265 0.035 7.674 0.000 0.265 0.257
.y1 0.302 0.026 11.558 0.000 0.302 0.555
.y2 0.285 0.027 10.634 0.000 0.285 0.438
.y3 0.362 0.031 11.854 0.000 0.362 0.620
YARIGAI 0.568 0.068 8.304 0.000 1.000 1.000
NINKAN 0.596 0.073 8.113 0.000 1.000 1.000
.MANZOKU -0.038 0.010 -3.722 0.000 -0.158 -0.158
R-Square:
Estimate
x1 0.690
x2 0.649
x3 0.535
x4 0.652
x5 0.556
x6 0.743
y1 0.445
y2 0.562
y3 0.380
MANZOKU NA1. モデル全体の評価(モデル適合度)
まず、仮説モデルが、収集したデータ全体とどれくらいよく一致しているか(=適合しているか)を確認します。これは、モデル全体の成績表のようなものです。
Model Test User Model:
Test statistic 19.690
Degrees of freedom 24
P-value (Chi-square) 0.714
User Model versus Baseline Model:
Comparative Fit Index (CFI) 1.000
Tucker-Lewis Index (TLI) 1.005
Root Mean Square Error of Approximation:
RMSEA 0.000
Standardized Root Mean Square Residual:
SRMR 0.025- カイ二乗検定 (Chi-square Test):
P-valueが0.714となっています。カイ二乗検定では「モデルとデータに差がない(=モデルはデータに適合している)」という仮説を検定します。P値が有意水準(ここでは5%とします)を超えていますので、仮説は棄却されません。 - 適合度指標 (Fit Indices): カイ二乗検定はサンプルサイズが大きいと有意になりやすい性質があるため、以下の指標も合わせて評価します。
- CFI / TLI: これらは1に近いほど良い指標です。基準は0.95以上が望ましいとされます。今回はそれぞれ1.000と1.005であり、良い適合度であると示唆されます。
- RMSEA: これは0に近いほど良い指標です。基準は0.05以下で良好、0.08以下で許容範囲とされます。今回は0.000であり、良好な適合度です。
- SRMR: これも0に近いほど良い指標です。基準は0.08以下が望ましいとされます。今回は0.025であり、基準を満たしています。
- 結論: 上記のすべての指標が良好な値を示していることから、「仕事のやりがいと職場の人間関係が仕事満足度を高める」というモデルは、データと適合していると結論できます。
2. 個別の関係性の評価(パラメータ推定値)
次に、モデルの内部を見て、具体的にどの関係が強いのか、仮説は支持されたのかを詳細に確認します。ここでは特に「Std.all」という列の標準化係数に注目します。これは影響の強さを-1から+1の範囲で示しており、異なる変数間の影響力を比較するのに便利です。
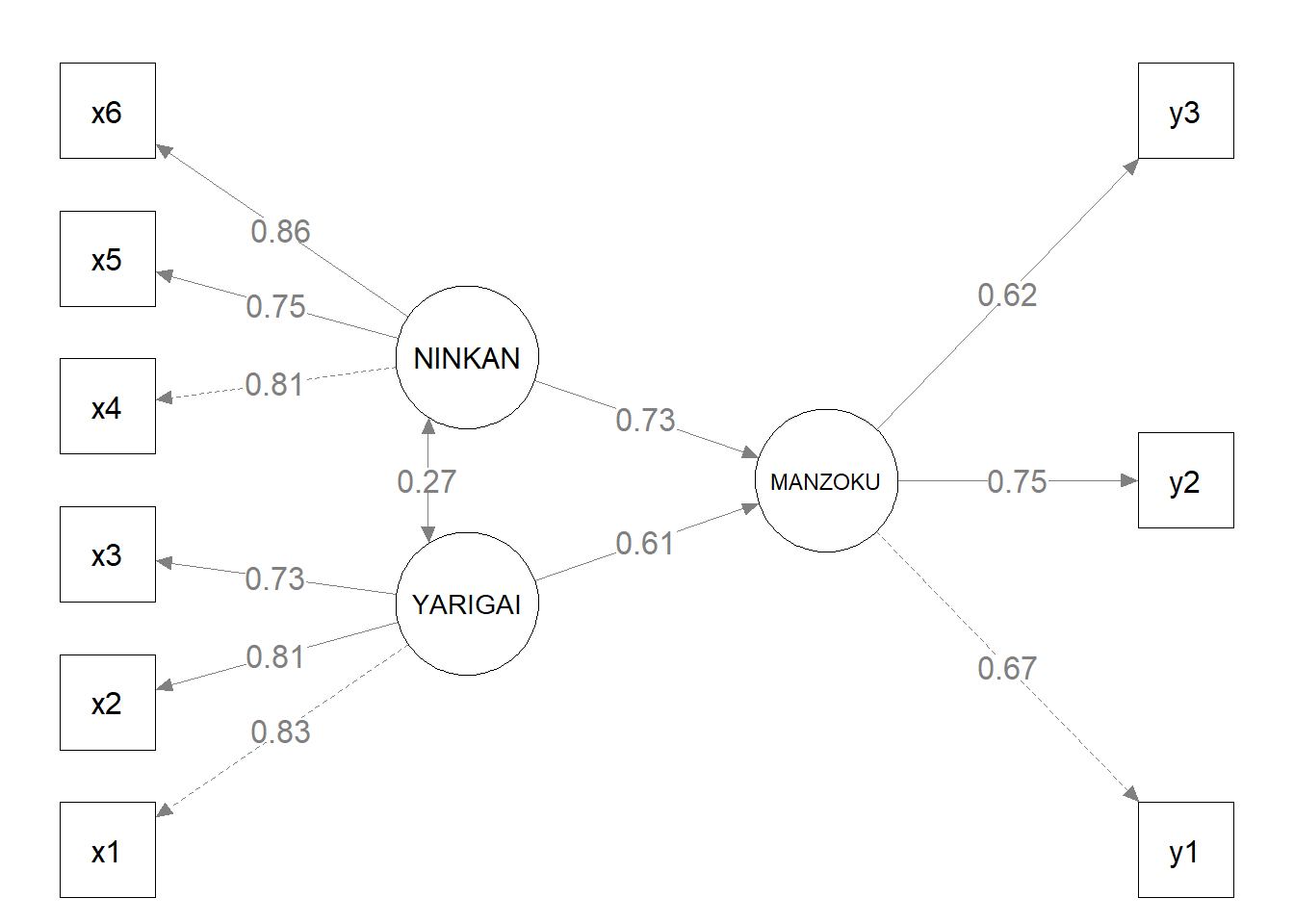
(1) 測定モデルの評価(Latent Variables)
各潜在変数(概念)が、アンケート項目(観測変数)によってうまく測定できているかを確認します。
Latent Variables:
Estimate ... Std.all
YARIGAI =~
x1 1.000 0.831
x2 0.987 0.805
x3 0.833 0.731
NINKAN =~
x4 1.000 0.807
x5 0.818 0.745
x6 1.133 0.862
MANZOKU =~
y1 1.000 0.667
y2 1.227 0.749
y3 0.956 0.616-
Std.allの値(標準化因子負荷量)が、それぞれの項目とその背後にある概念との関連の強さを示します。一般的に0.5以上あれば、その項目は概念をよく反映しているとされます。 - 仕事のやりがい (YARIGAI): 3つの項目(x1, x2, x3)の負荷量はいずれも0.7以上であり、これらの質問項目で「仕事のやりがい」を適切に測定できていると言えます。
- 職場の人間関係 (NINKAN) と 仕事満足度 (MANZOKU) も同様に、すべての項目の負荷量が高く、測定は適切である判断できます。
(2) 構造モデルの評価(Regressions)
ここでは、仮説が支持されたかどうかを検証します。
Regressions:
Estimate ... P(>|z|) ... Std.all
MANZOKU ~
YARIGAI 0.401 0.000 0.614
NINKAN 0.466 0.000 0.731- MANZOKU ~ YARIGAI: 「仕事のやりがい」から「仕事満足度」へのパスです。
-
P(>|z|)(p値)は0.000であり、有意水準を下回っているため、この関係は統計的に有意です。 -
Std.all(標準化パス係数)は0.614です。これは、「仕事のやりがい」が高まると、「仕事満足度」も高まるという正の関係があることを意味します。仮説は支持されました。
-
- MANZOKU ~ NINKAN: 「職場の人間関係」から「仕事満足度」へのパスです。
- p値は0.000であり、この関係も有意です。
- 標準化パス係数は0.731と、こちらも正の関係を示しています。「職場の人間関係」が良好であるほど、「仕事満足度」が高まるという仮説も支持されました。
- 影響力の比較: 標準化係数の大きさを比較すると、人間関係(0.731)の方がやりがい(0.614)よりも少し値が大きいです。このことから、今回のデータにおいては、仕事満足度に対して「仕事のやりがい」よりも「職場の人間関係」の方がやや影響力が大きい可能性が示唆されます。
3. 総合的な結論
今回の構造方程式モデリングの結果をまとめると、以下のようになります。
- モデルの妥当性: 「仕事のやりがい」と「職場の人間関係」が「仕事満足度」に影響を与えるというモデルは、データに適合しており、妥当なモデルであると言えます。
- 仮説の支持: 当初立てた2つの仮説、①「やりがいは満足度を高める」、②「人間関係は満足度を高める」は、いずれも有意に支持されました。
- 結論と示唆: 従業員の仕事満足度を向上させるためには、「仕事のやりがいを感じられるような業務設計」と「良好な職場の人間関係を促進する施策」の両方が重要であることがデータから示されました。特に、今回の分析からは「職場の人間関係」が満足度に与える影響が、より大きい可能性も示唆されています。
続いて、関数 parameterEstimates により、分析結果をより詳細に確認します。
# パラメータ推定値の解釈
param_estimates <- parameterEstimates(fit, standardized = TRUE)
param_estimates lhs op rhs est se z pvalue ci.lower ci.upper std.lv std.all
1 YARIGAI =~ x1 1.000 0.000 NA NA 1.000 1.000 0.753 0.831
2 YARIGAI =~ x2 0.987 0.067 14.836 0 0.857 1.117 0.744 0.805
3 YARIGAI =~ x3 0.833 0.063 13.287 0 0.710 0.956 0.628 0.731
4 NINKAN =~ x4 1.000 0.000 NA NA 1.000 1.000 0.772 0.807
5 NINKAN =~ x5 0.818 0.060 13.720 0 0.701 0.935 0.632 0.745
6 NINKAN =~ x6 1.133 0.070 16.267 0 0.997 1.270 0.875 0.862
7 MANZOKU =~ y1 1.000 0.000 NA NA 1.000 1.000 0.492 0.667
8 MANZOKU =~ y2 1.227 0.100 12.270 0 1.031 1.423 0.604 0.749
9 MANZOKU =~ y3 0.956 0.093 10.295 0 0.774 1.138 0.471 0.616
10 MANZOKU ~ YARIGAI 0.401 0.038 10.678 0 0.327 0.475 0.614 0.614
11 MANZOKU ~ NINKAN 0.466 0.041 11.510 0 0.387 0.546 0.731 0.731
12 x1 ~~ x1 0.255 0.032 7.964 0 0.192 0.318 0.255 0.310
13 x2 ~~ x2 0.300 0.034 8.685 0 0.232 0.367 0.300 0.351
14 x3 ~~ x3 0.343 0.034 10.077 0 0.276 0.410 0.343 0.465
15 x4 ~~ x4 0.318 0.034 9.291 0 0.251 0.386 0.318 0.348
16 x5 ~~ x5 0.319 0.031 10.310 0 0.258 0.380 0.319 0.444
17 x6 ~~ x6 0.265 0.035 7.674 0 0.198 0.333 0.265 0.257
18 y1 ~~ y1 0.302 0.026 11.558 0 0.251 0.353 0.302 0.555
19 y2 ~~ y2 0.285 0.027 10.634 0 0.232 0.337 0.285 0.438
20 y3 ~~ y3 0.362 0.031 11.854 0 0.302 0.422 0.362 0.620
21 YARIGAI ~~ YARIGAI 0.568 0.068 8.304 0 0.434 0.702 1.000 1.000
22 NINKAN ~~ NINKAN 0.596 0.073 8.113 0 0.452 0.740 1.000 1.000
23 MANZOKU ~~ MANZOKU -0.038 0.010 -3.722 0 -0.058 -0.018 -0.158 -0.158
24 YARIGAI ~~ NINKAN 0.160 0.041 3.846 0 0.078 0.241 0.274 0.2744. パラメータ推定値の解釈
上記の表は、構造方程式モデリング(SEM)で推定されたすべてのパラメータ(パス係数、分散、共分散など)をリストアップしたものです。
まず、表の各列の意味を簡単に説明します。
-
lhs: 左辺 (Left-Hand Side) の変数 -
op: 演算子。関係性の種類を示します。-
=~: 測定モデル。潜在変数が観測変数によって測定される関係。 -
~: 回帰(構造モデル)。左辺の変数が右辺の変数から影響を受ける関係。 -
~~: 分散・共分散。変数のばらつきや、変数間の相関。
-
-
rhs: 右辺 (Right-Hand Side) の変数 -
est: 非標準化係数。元のデータの尺度での推定値。 -
se: 標準誤差。推定値のばらつきの大きさ。 -
z: z値。est / seで計算され、係数が0と有意に異なるか検定するために使われます。 -
pvalue: p値。この関係が統計的に有意かどうかを示します。 -
ci.lower/ci.upper: 95%信頼区間の下限と上限。この区間に0を含まない場合、その係数は統計的に有意であると解釈できます。 -
std.all: 標準化係数。変数のばらつきを揃えた(標準化した)後の係数で、-1から+1の値をとり、影響の強さを比較する際の指標です。
それでは、結果を3つのパートに分けて見ていきましょう。
1. 測定モデルの評価(1行目〜9行目)
演算子 =~ の部分です。各潜在変数が、対応するアンケート項目でどの程度うまく測定できているかを示します。
lhs op rhs ... std.all
1 YARIGAI =~ x1 ... 0.831
2 YARIGAI =~ x2 ... 0.805
3 YARIGAI =~ x3 ... 0.731
4 NINKAN =~ x4 ... 0.807-
std.all列の値は標準化因子負荷量と呼ばれ、各項目とそれが測定しようとしている概念との関連の強さを示します。 - 例えば1行目は、「仕事のやりがい(YARIGAI)」とアンケート項目「x1(仕事への興味・関心)」の関連の強さが0.831であることを意味します。
- すべての項目の
std.allが0.5以上を示しており、pvalueもすべて0です(estが1.0と、基準変数であるx1、x4、y1は除きます)。これは、3つの潜在変数(やりがい、人間関係、満足度)が、それぞれ意図したアンケート項目群によって適切に測定できていることを示しています。
2. 構造モデルの評価(10行目〜11行目)
演算子 ~ の部分です。ここが、検証したい仮説に対応する部分です。
lhs op rhs ... pvalue ... std.all
10 MANZOKU ~ YARIGAI ... 0 0.614
11 MANZOKU ~ NINKAN ... 0 0.731- 10行目 (YARIGAI → MANZOKU):
-
pvalueが0であり(95%信頼区間[0.327, 0.475]は0を含んでいない)、この関係は有意です。 -
std.all(標準化パス係数)は0.614です。これは、「仕事のやりがい」が「仕事満足度」に対して、正の影響を与えていることを示します。
-
- 11行目 (NINKAN → MANZOKU):
- こちらも
pvalueが0ですので(信頼区間[0.387, 0.546]は0を含んでいない)、有意な関係です。 -
std.allは0.731であり、「職場の人間関係」が「仕事満足度」に対して、正の影響を与えていることを示します。
- こちらも
- 当初の仮説であった「やりがい → 満足度」、「人間関係 → 満足度」は、両方ともデータによって支持されました。標準化係数を比較すると、人間関係(0.731)の方がやりがい(0.614)よりも影響力が大きいことがわかります。
3. 分散と共分散の評価(12行目〜24行目)
演算子 ~~ の部分です。モデル内の各変数のばらつき(分散)や、変数間の相関(共分散)を示しています。
lhs op rhs est ... std.all
...
12 x1 ~~ x1 0.255 ... 0.310
...
24 YARIGAI ~~ NINKAN 0.160 ... 0.274- 12~20行目(誤差分散)
-
x1 ~~ x1のように同じ観測変数が並んでいるのは、測定誤差の分散を表します。例えばstd.allが0.310ということは、観測変数x1のばらつきのうち、約31%が潜在変数「YARIGAI」では説明できない誤差(個人差や回答のゆらぎなど)であることを意味します。
-
- 24行目(潜在変数の共分散)
-
YARIGAI ~~ NINKANは、「仕事のやりがい」と「職場の人間関係」の間の相関関係を示します。 -
pvalueが0.000と有意であり、std.allが0.274となっています。これは、「仕事のやりがい」と「職場の人間関係」の間には、統計的に意味のある正の相関があることを示しています。つまり、やりがいを感じている人ほど、人間関係も良好である傾向がある、ということです。
-
# 6. 可視化:semPaths()関数でパス図を描画
# ------------------------------------------------
semPaths(
object = fit,
whatLabels = "std",
layout = "tree",
rotation = 2,
edge.label.cex = 1.2,
residuals = FALSE,
sizeMan = 8,
sizeLat = 12,
style = "ram",
nCharNodes = 0,
mar = c(2, 2, 3, 2)
)- 四角は観測変数(アンケート項目)、楕円は潜在変数(概念)です。
以上です。