Rの関数から density {stats} を確認します。
カーネル密度推定とは?
カーネル密度推定は、観測されたデータから、その背後にある真の分布を滑らかな曲線で推定するためのノンパラメトリック手法です。
データの分布を把握したいときに多く利用される、ヒストグラムはデータをいくつかの区間(ビン)に区切り、各区間に含まれるデータの数を棒グラフで表したものです。
カーネル密度推定は、このヒストグラムの「上位互換」のような手法と考えると分かりやすいでしょう。
カーネル密度推定の基本的な考え方
カーネル密度推定は、以下の3つのステップで滑らかな曲線を描きます。
ステップ1:各データ点の上に「小さな山」を置く
まず、観測されたデータ点一つひとつに注目します。そして、それぞれのデータ点を中心として、カーネル関数と呼ばれる「小さな山(釣鐘状のカーブなど)」を置きます。
x軸上にデータ点があり、それぞれの真上に小さな釣鐘状のカーブが描かれているイメージです。
多く利用されるのは、平均が0の正規分布(ガウス分布)の形をしたガウスカーネルです。ちょうど、データ点がある場所を頂点にした釣鐘状のカーブをイメージしてください。
ステップ2:すべての「山」を足し合わせる
次に、ステップ1で置いたすべての小さな山(カーネル関数)を、単純に足し合わせます。データが密集している場所では、たくさんの山が重なり合いますので、結果として大きな山ができます。逆に、データがまばらな場所では、山が低くなります。
ガウスカーネルの場合は、小さな釣鐘状のカーブがすべて合計され、一つの滑らかな曲線になっているイメージです。
ステップ3:正規化する
最後に、足し合わせた曲線の全体の面積が「1」になるように、全体の高さを調整します(データ数で割るなど)。これにより、確率密度関数として扱うことができるようになります。
この最終的に出来上がった滑らかな曲線が、カーネル密度推定によって得られたデータの分布です。
最も重要なパラメータ:「バンド幅(bandwidth)」
カーネル密度推定で最も重要であるのがバンド幅というパラメータです。これは、ステップ1で置いた「小さな山」の幅(太さ)を決定します。
- バンド幅が小さい場合:
- 山が細く、鋭くなります。
- 曲線はギザギザになり、個々のデータ点の影響を強く受けます。
- データの細かい特徴を捉えすぎ、ノイズまで拾ってしまう「過剰適合」の状態になりがちです。
- バンド幅が大きい場合:
- 山が太く、なだらかになります。
- 曲線は非常に滑らかになります。
- データの細かな構造(例えば、複数のピーク)が隠れてしまい、分布を単純化しすぎる「過小適合」の状態になりがちです。
ヒストグラムにおける「ビンの幅」と同様に、このバンド幅を適切に選ぶことが、カーネル密度推定をうまく使う上で重要です。
関数density {stats}の確認
args(density.default)function (x, bw = "nrd0", adjust = 1, kernel = c("gaussian",
"epanechnikov", "rectangular", "triangular", "biweight",
"cosine", "optcosine"), weights = NULL, window = kernel,
width, give.Rkern = FALSE, subdensity = FALSE, warnWbw = var(weights) >
0, n = 512, from, to, cut = 3, ext = 4, old.coords = FALSE,
na.rm = FALSE, ...)
NULL| 引数名 | デフォルト値 | 説明 |
|---|---|---|
x | – | 入力データ。密度を推定したい数値ベクトルを指定します。 |
bw | “nrd0” | バンド幅(bandwidth)。カーネルの「幅」を制御する最も重要なパラメータです。数値を直接指定するほか、文字列で自動選択アルゴリズムを指定できます(例: “nrd0”はSilvermanの経験則)。 |
adjust | 1 | バンド幅の調整係数。bwで決まったバンド幅にこの値を掛け合わせます。adjustを大きくすると曲線はより滑らかに、小さくするとよりギザギザになります。 |
kernel | “gaussian” | カーネル関数の種類。カーネルの「山の形」を決めます。デフォルトはガウスカーネル(正規分布)で、他にも“epanechnikov”, “rectangular”など複数の種類から選択できます。 |
weights | NULL | 各データ点への重み。xの各点に異なる重要度を与えたい場合に、xと同じ長さのベクトルで指定します。デフォルトは全データ点が同じ重みを持ちます。 |
n | 512 | 評価点の数。密度を計算する等間隔のグリッド(点)の数です。この値を大きくすると、より滑らかで解像度の高い曲線が得られますが、計算コストが増加します。 |
from, to | (自動計算) | 密度の計算範囲。x軸のどこからどこまでを計算するかを指定します。未指定の場合は、データの最小値・最大値から自動的に設定されます。 |
cut | 3 | fromとtoを自動計算する際の拡張係数。from = min(x) - cut * bw のように、データの範囲をバンド幅のcut倍だけ外側に広げます。ガウスカーネルの場合、3倍のバンド幅の外側はほぼ0になるため、デフォルトは3です。 |
na.rm | FALSE | 欠損値の扱い。TRUEにすると、xに含まれる欠損値(NA)を計算前に自動的に除去します。FALSE(デフォルト)の場合、NAが含まれているとエラーになります。 |
カーネル関数とは?
カーネル関数とは、カーネル密度推定において「各データ点の上に置く、小さな山の形」を定義するものです。どのカーネルを選ぶかによって、最終的に得られる密度曲線の滑らかさや形状が微妙に変わります。
ただし、実用上はカーネルの種類の選択よりも、バンド幅 (bw) の選択の方がはるかに結果に大きな影響を与えます。
カーネル関数のシミュレーション
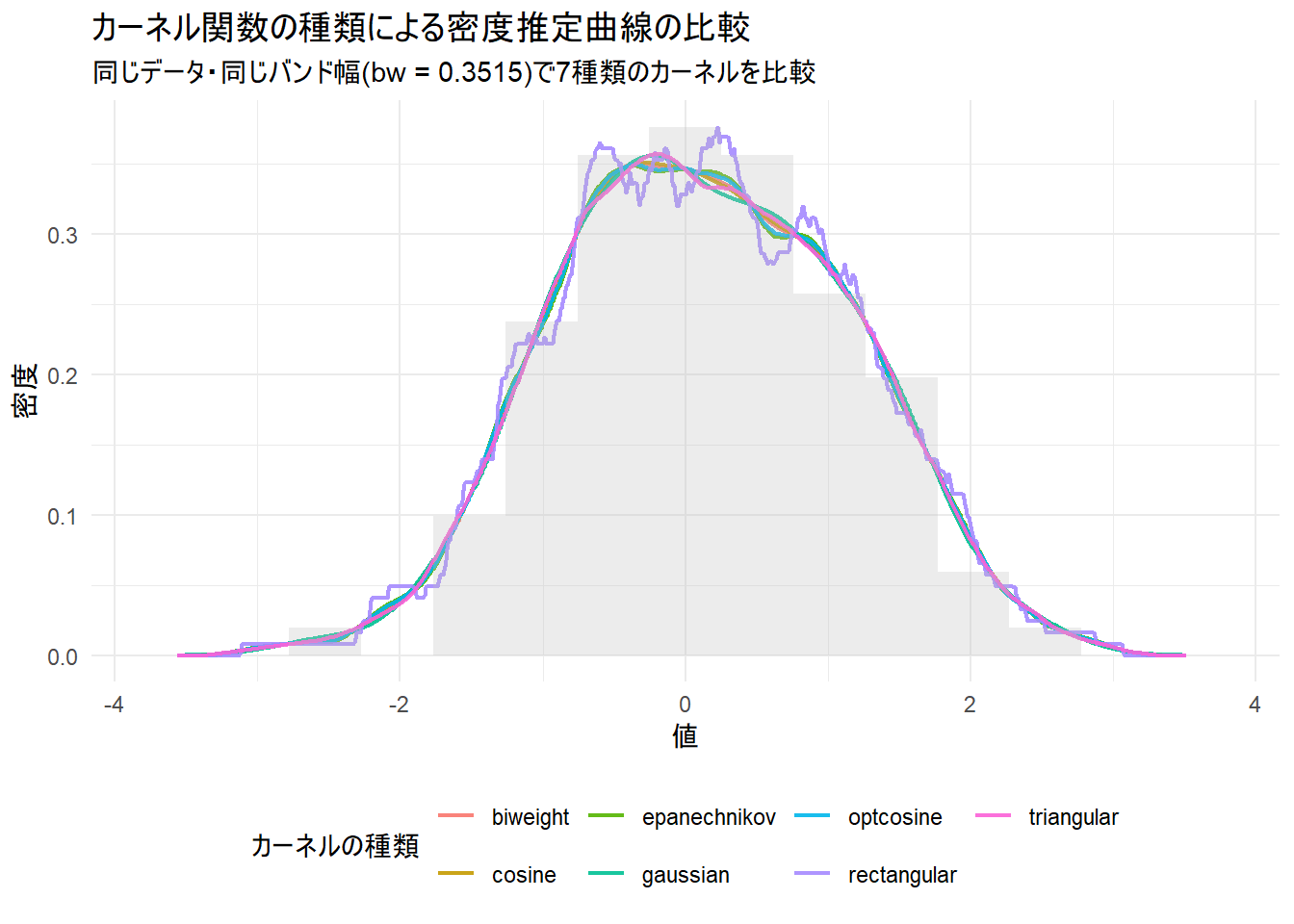
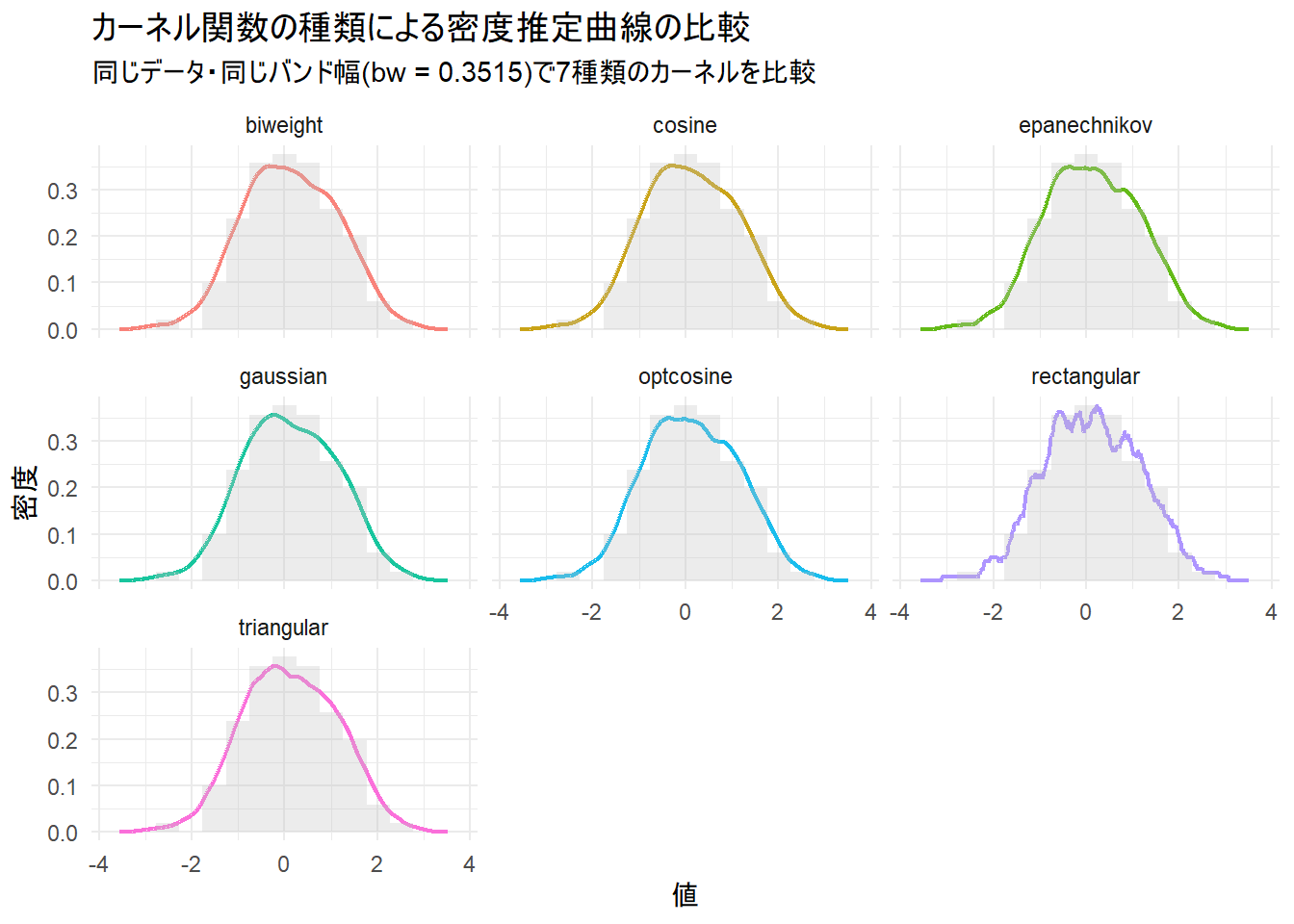
このシミュレーションでは、同じデータと同じバンド幅(bw)を使い、kernel引数だけを変更した場合に、カーネル密度推定の曲線がどのように変化するかを視覚的に比較します。
サンプルデータは、標準正規分布から生成した100個のデータ点を使用します。
# 必要なライブラリを読み込みます
library(ggplot2)
library(purrr)
library(dplyr)
# --- 1. データの準備 ---
# 再現性を確保するために乱数シードを設定します
seed <- 20250902
set.seed(seed)
# 標準正規分布に従う100個の乱数を生成します
sim_data <- rnorm(100, mean = 0, sd = 1)
# --- 2. 各カーネルで密度推定を実行 ---
# 比較するカーネルの種類のリストを作成します
kernel_types <- c(
"gaussian", "epanechnikov", "rectangular", "triangular",
"biweight", "cosine", "optcosine"
)
# 公平な比較のため、全てのカーネルで同じバンド幅を使用します
# ここではRのデフォルトのアルゴリズム "nrd0" でバンド幅を計算します
common_bw <- bw.nrd0(sim_data)
# purrr::map_dfr を使い、各カーネルでdensity()を実行し、結果を一つのデータフレームにまとめます
density_df <- map_dfr(kernel_types, ~ {
# density関数で推定を実行
d <- density(sim_data, kernel = .x, bw = common_bw, n = 1024)
# ggplotで扱いやすいように、x座標、y座標、カーネルの種類を持つデータフレームに変換
data.frame(
x = d$x,
y = d$y,
kernel_type = .x
)
})
# --- 3. ggplot2で結果をプロット ---
# カーネルの種類ごとに色分けして、密度曲線を重ねて描画します
g <- ggplot(density_df, aes(x = x, y = y, color = kernel_type)) +
geom_line(linewidth = 0.8, alpha = 0.9) +
# 元のデータの分布が分かりやすいように、ヒストグラムを背景に薄く描画します
geom_histogram(
data = data.frame(x = sim_data),
aes(x = x, y = after_stat(density)),
inherit.aes = FALSE,
bins = 15,
fill = "gray",
alpha = 0.3
) +
labs(
title = "カーネル関数の種類による密度推定曲線の比較",
subtitle = paste0("同じデータ・同じバンド幅(bw = ", round(common_bw, 4), ")で7種類のカーネルを比較"),
x = "値",
y = "密度",
color = "カーネルの種類"
) +
theme_minimal() +
theme(legend.position = "bottom")
g
g + facet_wrap(. ~ kernel_type) + theme(legend.position = "none") バンド幅(bw)のシミュレーション
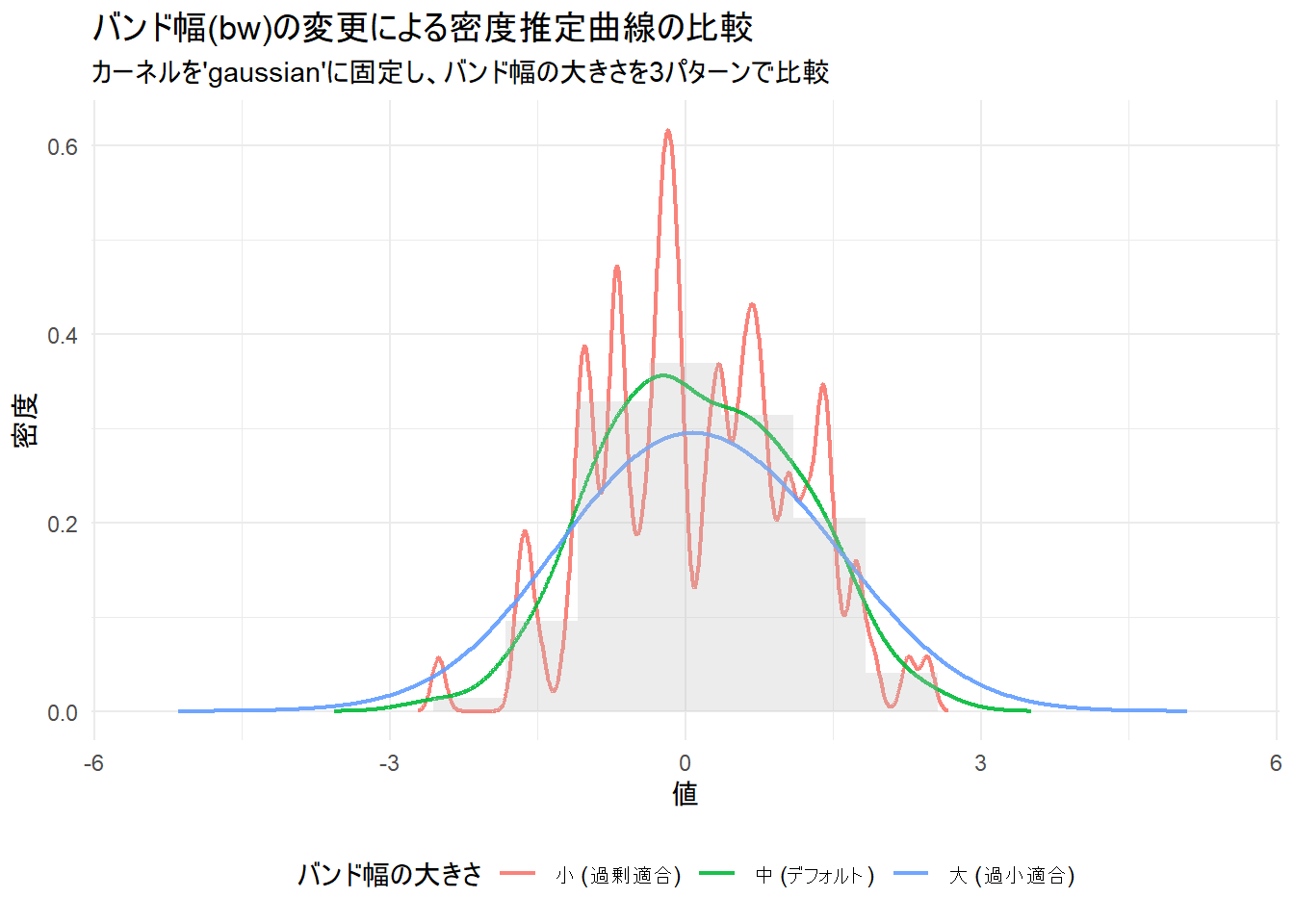
カーネル密度推定において最も重要なパラメータであるバンド幅(bw)が、推定される密度曲線にどのような影響を及ぼすかを視覚的に理解します。バンド幅を「小さすぎる場合」、「適切な場合」、「大きすぎる場合」の3つのシナリオで比較します。
# --- 1. データの準備 ---
set.seed(seed)
sim_data <- rnorm(100, mean = 0, sd = 1)
# --- 2. 比較するバンド幅を設定 ---
# Rのデフォルトアルゴリズム("nrd0")で計算されるバンド幅を基準とします
bw_default <- bw.nrd0(sim_data)
# 比較のために3種類のバンド幅を用意します
bw_list <- list(
"小 (過剰適合)" = bw_default * 0.2,
"中 (デフォルト)" = bw_default,
"大 (過小適合)" = bw_default * 2.5
)
cat("比較に使用するバンド幅の値:\n")
# 各バンド幅の具体的な値を表示します
walk2(names(bw_list), bw_list, ~ cat(paste0(.x, ": bw = ", round(.y, 4), "\n")))
# --- 3. 各バンド幅で密度推定を実行 ---
# purrr::map_dfrを使い、各バンド幅でdensity()を実行し、結果を一つのデータフレームにまとめます
density_df <- map_dfr(names(bw_list), ~ {
# density関数を実行。kernelは"gaussian"に固定
d <- density(sim_data, bw = bw_list[[.x]], kernel = "gaussian", n = 1024)
data.frame(
x = d$x,
y = d$y,
bw_label = .x # バンド幅のラベル
)
})
# 凡例の順序を意図通りにするため、factor型に変換します
density_df$bw_label <- factor(density_df$bw_label, levels = names(bw_list))
# --- 4. ggplot2で結果をプロット ---
# バンド幅のラベルごとに色分けして、密度曲線を重ねて描画します
ggplot(density_df, aes(x = x, y = y, color = bw_label)) +
geom_line(linewidth = 0.8, alpha = 0.9) +
# 元のデータの分布が分かりやすいように、ヒストグラムを背景に薄く描画します
geom_histogram(
data = data.frame(x = sim_data),
aes(x = x, y = after_stat(density)),
inherit.aes = FALSE,
bins = 15,
fill = "gray",
alpha = 0.3
) +
labs(
title = "バンド幅(bw)の変更による密度推定曲線の比較",
subtitle = "カーネルを'gaussian'に固定し、バンド幅の大きさを3パターンで比較",
x = "値",
y = "密度",
color = "バンド幅の大きさ"
) +
theme_minimal() +
theme(legend.position = "bottom")比較に使用するバンド幅の値:
小 (過剰適合): bw = 0.0703
中 (デフォルト): bw = 0.3515
大 (過小適合): bw = 0.8788以上です。