Rの関数から adf.test {tseries} を確認します。
adf.test関数について
adf.testは、拡張ディッキー–フラー検定(Augmented Dickey-Fuller Test) を実行するための関数です。この検定の目的は、時系列データが単位根(unit root) を持つかどうかを統計的に判断することです。
時系列データに単位根が存在する場合、そのデータは非定常(non-stationary)であるとされます。
非定常な時系列は、時間とともに平均や分散が変化する、いわゆるランダムウォークのような性質を持ちます。
一方で、単位根が存在しない場合は定常(stationary)である可能性があり、その時系列は長期的に見て一定の平均値の周りを変動する性質を持ちます。
データが定常であることを前提としている時系列分析手法を採用する場合は、分析の前に単位根検定によりデータの定常性を確認することが重要な工程になります。
adf.test における仮説は以下の通りです。
- 帰無仮説 (H₀): 単位根が存在する(時系列は非定常である)。
- 対立仮説 (H₁): 単位根が存在しない(時系列は定常、または発散過程である)。
検定結果のp値が、あらかじめ設定した有意水準(例えば0.05)よりも小さい場合、帰無仮説は棄却され、「データは定常である」と結論付けられます。
adf.test関数の引数について
library(tseries)
args(adf.test)function (x, alternative = c("stationary", "explosive"), k = trunc((length(x) -
1)^(1/3)))
NULLx
検定の対象となる数値ベクトル、または時系列オブジェクトを指定します。分析したい時系列データをこの引数に渡します。
alternative
対立仮説の種類を指定する引数です。以下の2つから選択します。
"stationary"(デフォルト): 対立仮説を「時系列は定常である」と設定します。p値が設定した有意水準より小さい場合に、データは定常であると判断されます。"explosive": 対立仮説を「時系列は発散過程である」と設定します。発散過程とは、時間とともに値が指数関数的に発散していくような時系列を指します。こちらもp値が有意水準より小さい場合に、データは発散過程であると判断されます。
k
検定の回帰式に含めるラグ(lag) の次数を指定します。拡張ディッキー–フラー検定では、時系列の持つ自己相関を考慮するために、自身の過去の値との差分(ラグ)を説明変数に加えます。適切なラグ次数 k を選択することは、検定の信頼性を担保する上で重要です。
デフォルトでは、trunc((length(x) - 1)^(1/3)) というSchwertの提案による経験則に基づいて、データの長さに応じたラグ次数が自動的に計算されます。
シミュレーション
adf.test関数の挙動を確認するために、シミュレーションを実行します。
ここでは意図的に「非定常なデータ」と「定常なデータ」を作成し、それぞれにadf.testを適用して結果を比較します。
# 再現性を確保するために乱数のシードを設定します
seed <- 20251009
set.seed(seed)
# データポイントの数を定義します
n <- 250
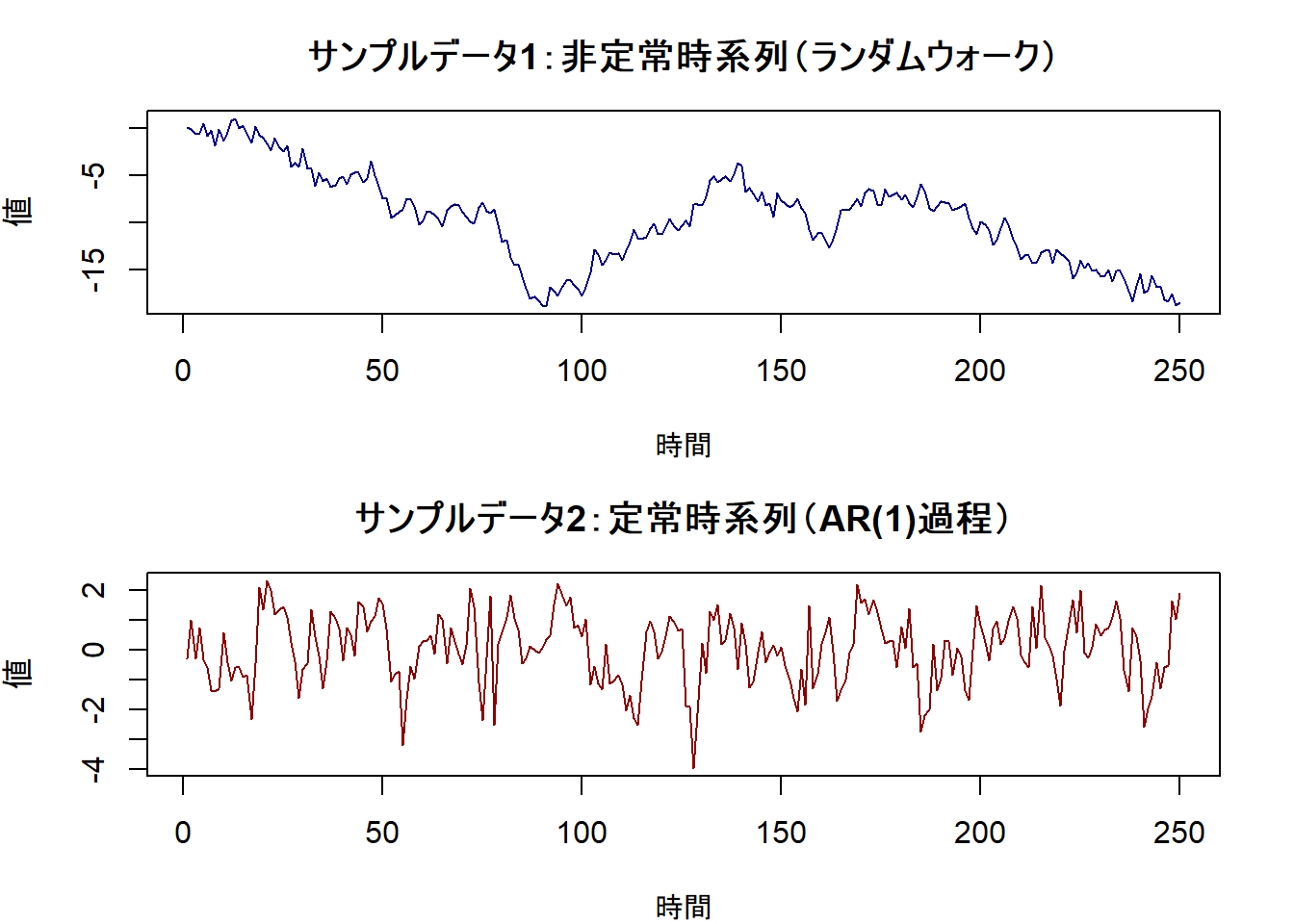
# 1. 非定常な時系列データ(ランダムウォーク)を作成します
# 単位根を持つ時系列の代表例です
# 前期の値に正規乱数を足し合わせていくことで生成されます
non_stationary_data <- cumsum(rnorm(n))
# 2. 定常な時系列データ(AR(1)過程)を作成します
# 自己回帰係数|φ|<1のAR(1)モデルは、定常過程の代表例です
stationary_data <- arima.sim(model = list(ar = 0.6), n = n)
# 描画デバイスの設定
# 1つのウィンドウに縦に2つのプロットを並べます
par(mfrow = c(2, 1), mar = c(4, 4, 3, 2))
# 非定常データをプロットします
plot(non_stationary_data,
type = "l", col = "darkblue",
main = "サンプルデータ1:非定常時系列(ランダムウォーク)",
xlab = "時間", ylab = "値"
)
# 定常データをプロットします
plot(stationary_data,
type = "l", col = "darkred",
main = "サンプルデータ2:定常時系列(AR(1)過程)",
xlab = "時間", ylab = "値"
)cat("--- ケース1:非定常データに対する検定 ---\n")
# adf.testの帰無仮説は「単位根が存在する(非定常である)」です。
# 非定常データですので、p値は大きくなり、帰無仮説は棄却されないと予測されます。
adf_result1 <- adf.test(non_stationary_data)
print(adf_result1)
cat("--- ケース2:定常データに対する検定 ---\n")
# 定常データですので、p値は小さくなり、
# 帰無仮説が棄却され、対立仮説「定常である」が採択されると予測されます。
adf_result2 <- adf.test(stationary_data)
print(adf_result2)--- ケース1:非定常データに対する検定 ---
Augmented Dickey-Fuller Test
data: non_stationary_data
Dickey-Fuller = -1.9378, Lag order = 6, p-value = 0.602
alternative hypothesis: stationary
--- ケース2:定常データに対する検定 ---
Augmented Dickey-Fuller Test
data: stationary_data
Dickey-Fuller = -5.8389, Lag order = 6, p-value = 0.01
alternative hypothesis: stationary- ケース1の非定常データに対する検定の結果、p値は
0.602と有意水準を超えました。よって、帰無仮説「単位根が存在する」は棄却できず、データが非定常であることを示唆しています。 - ケース2の定常データに対する検定の結果、p値は
0.01と有意水準を下回りました。よって、帰無仮説「単位根が存在する」は棄却され、データが定常であることを示唆しています。
alternative引数による対立仮説の違い
1. alternative = "stationary" (デフォルト)
- 帰無仮説 (H₀): 単位根が存在する (ρ = 1)。
- 対立仮説 (H₁): 時系列は定常である (ρ < 1)。
この設定では、検定は「ρが1よりも小さいかどうか」を検証します。ρが1より小さい場合、時系列は過去の値の影響が時間とともに減衰していくため、平均に回帰する性質(定常性)を持ちます。ですので、p値が小さく帰無仮説が棄却された場合、「データは定常である」と結論付けます。
2. alternative = "explosive"
- 帰無仮説 (H₀): 単位根が存在する (ρ = 1)。
- 対立仮説 (H₁): 時系列は発散過程である (ρ > 1)。
こちらの設定では、検定は「ρが1よりも大きいかどうか」を検証します。ρが1より大きい場合、時系列は過去の値の影響が時間とともに増大していくため、値が発散していく性質を持ちます。ですので、p値が小さく帰無仮説が棄却された場合、「データは発散過程である」と結論付けます。
3. まとめ
要するに、adf.testは常に「このデータは単位根過程(ランダムウォーク)ですか?」という問いを基準点(帰無仮説)にしています。alternative引数は、「もし単位根過程でないとしたら、その代わりにどのような性質を想定しますか?(平均回帰的ですか、それとも発散していきますか?)」という、対抗馬となる仮説を指定する役割を果たします。
4. シミュレーションによる確認
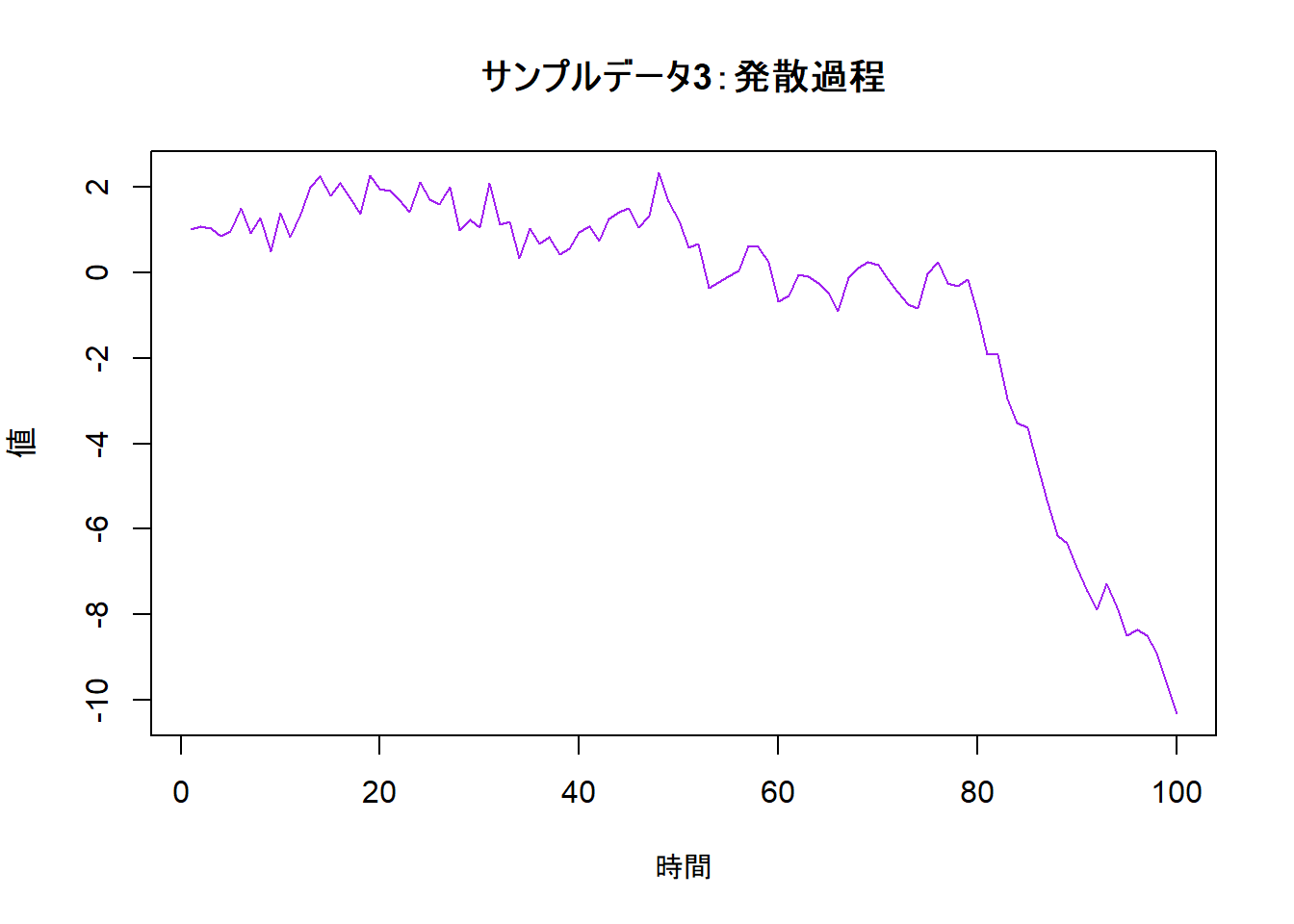
"explosive"なサンプルデータを作成し、alternative引数を変えて検定を実行してみましょう。
# 再現性を確保するために乱数のシードを設定します
set.seed(seed)
# 発散過程のサンプルデータ作成
n <- 100
# 係数ρ > 1 となる自己回帰モデルを考えます
explosive_data <- numeric(n)
explosive_data[1] <- 1
# y[t] = 1.05 * y[t-1] + error
for (i in 2:n) {
explosive_data[i] <- 1.05 * explosive_data[i - 1] + rnorm(1, 0, 0.5)
}
# データをプロットして確認します
plot(explosive_data,
type = "l", col = "purple",
main = "サンプルデータ3:発散過程",
xlab = "時間", ylab = "値"
)cat("--- ケース1:alternative = 'stationary' で検定 ---\n")
# 対立仮説が「定常である」ですので、p値は大きくなり、
# 帰無仮説「単位根が存在する」は棄却されないと予測されます。
adf_result3_1 <- adf.test(explosive_data, alternative = "stationary")
print(adf_result3_1)
cat("--- ケース2:alternative = 'explosive' で検定 ---\n")
# 対立仮説が「発散過程である」ですので、p値は小さくなり、
# 帰無仮説「単位根が存在する」が棄却されると予測されます。
adf_result3_2 <- adf.test(explosive_data, alternative = "explosive")
print(adf_result3_2)--- ケース1:alternative = 'stationary' で検定 ---
Augmented Dickey-Fuller Test
data: explosive_data
Dickey-Fuller = 0.2186, Lag order = 4, p-value = 0.99
alternative hypothesis: stationary
--- ケース2:alternative = 'explosive' で検定 ---
Augmented Dickey-Fuller Test
data: explosive_data
Dickey-Fuller = 0.2186, Lag order = 4, p-value = 0.01
alternative hypothesis: explosive- ケース1の発散過程に対して alternative = ‘stationary’ で検定した場合、p値が0.99となり、帰無仮説は棄却されません。よって、「非定常ではない」とは言えず、「定常である」という結論には至りません。
- ケース2の発散過程に対して alternative = ‘explosive’で検定した場合、p値が0.01と有意水準を下回りましたので、帰無仮説を棄却します。よって、対立仮説である「データは発散過程である」ことを示唆しています。
発散過程と単位根過程の違い
発散過程と単位根過程は、どちらも非定常な時系列ですが、その振る舞いの性質にな違いがあります。
最も簡潔に表現すると、その違いは「過去からの影響をどの程度受け継ぎ、増幅させるか」にあります。
この違いを確認するために、両者の基礎となる単純な自己回帰モデル(AR(1)モデル) を見てみましょう。
yₜ = ρ * yₜ₋₁ + εₜ
この式は、「現在の値 (yₜ) は、直前の値 (yₜ₋₁) に係数 ρ (ロー) を掛けたものに、予測できないランダムな変動 (εₜ, ホワイトノイズ) を足して決まる」ことを示しています。発散過程と単位根過程の違いは、この係数 ρ の値によって定義されます。
単位根過程 (Unit Root Process): ρ = 1
- モデル式:
yₜ = yₜ₋₁ + εₜ - 振る舞い: この式はランダムウォークとして知られています。「次の位置は、現在の位置にランダムな一歩を加えたもの」という意味です。
- 過去からの影響: 過去の値
yₜ₋₁の影響をそのまま100%受け継ぎます。過去に受けたランダムな変動(ショック)は、減衰することなく未来永劫にわたって影響し続けます。つまり「ショックが恒久的(permanent)である」ことになります。 - 平均への回帰: 決まった平均値に戻ろうとする性質(平均回帰性)がありません。一度離れた場所から元の水準に戻る見込みは小さく、どこまでもランダムにさまよい続けます。
発散過程 (Explosive Process): ρ > 1
- モデル式:
yₜ = ρ * yₜ₋₁ + εₜ(ただしρ > 1) - 振る舞い: 「次の値は、現在の値を1倍以上に増幅させたものに、ランダムな変動を加えたもの」という意味になります。
- 過去からの影響: 過去の値の影響を100%以上に増幅させて受け継ぎます。過去に受けたショックは、時間とともにその影響が指数関数的に増大していきます。
- 平均への回帰: 平均に回帰するどころか、特定の方向(正または負)へ指数関数的に発散していきます。
対比のための参考:定常過程 (Stationary Process): |ρ| < 1
- モデル式:
yₜ = ρ * yₜ₋₁ + εₜ(ただし|ρ| < 1) - 振る舞い: 「次の値は、現在の値を1倍未満に減衰させたものに、ランダムな変動を加えたもの」です。
- 過去からの影響: 過去の値の影響は、時間とともに減衰していきます。過去に受けたショックの影響は一時的(transitory)であり、いずれ消滅します。
- 平均への回帰: 長期的な平均値の周りを変動する性質(平均回帰性)を持ちます。
まとめ
| 特性 | 単位根過程 (ρ = 1) | 発散過程 (ρ > 1) | 定常過程 ( |
|---|---|---|---|
| 別名 | ランダムウォーク | – | 平均回帰過程 |
| 過去の影響 | 減衰しない (100%維持) | 増大・増幅する | 減衰する |
| ショックの影響 | 恒久的 (Permanent) | 増幅的 (Amplifying) | 一時的 (Transitory) |
| 平均回帰性 | なし | なし(発散する) | あり |
| 振る舞い | ランダムに変動し続ける | 指数関数的に発散する | 平均の周りを変動する |
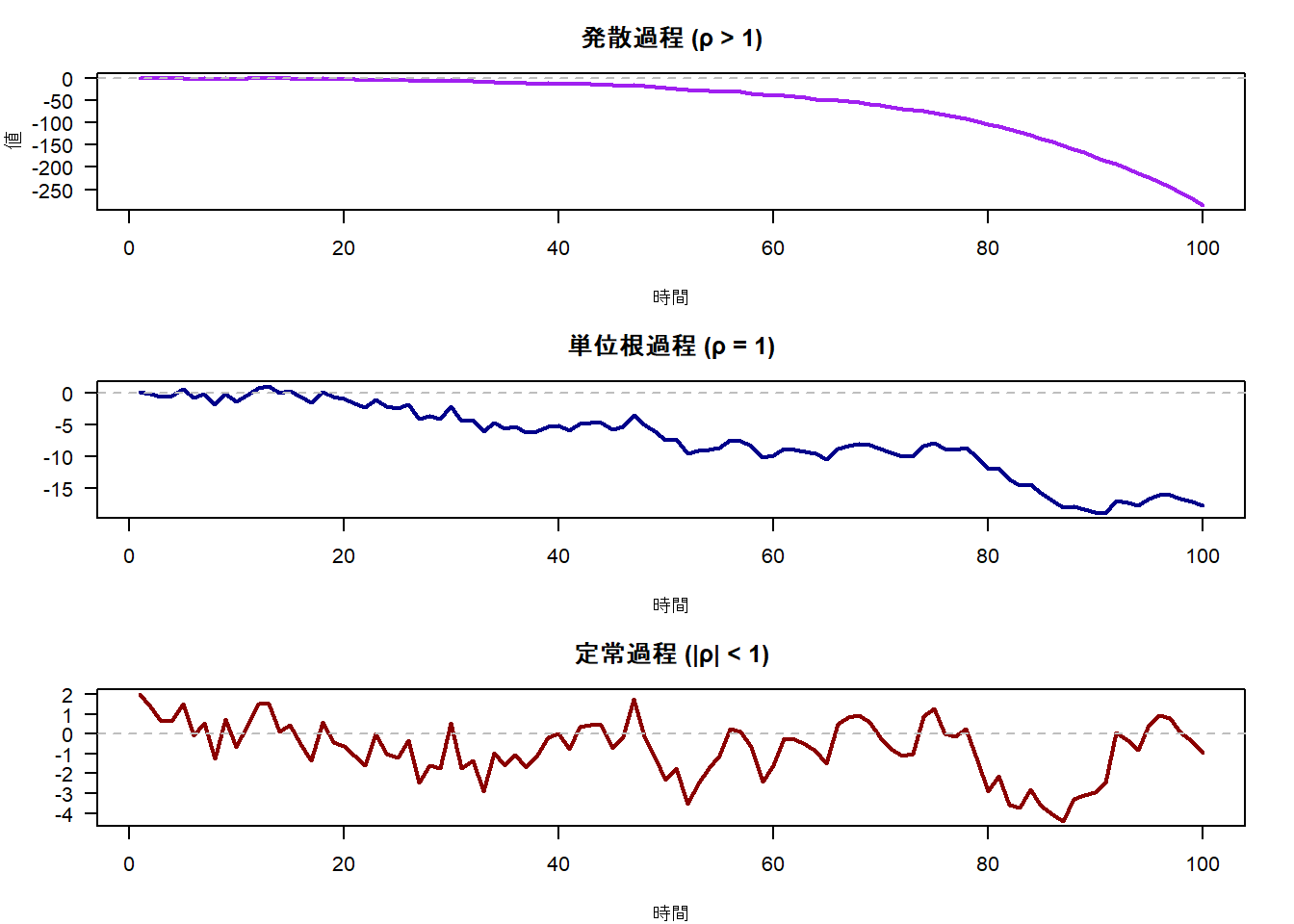
視覚的な比較
3つの過程をシミュレーションで比較します。
# 再現性を確保するために乱数のシードを設定します
set.seed(seed)
n <- 100 # データポイントの数
shocks <- rnorm(n, 0, 1) # 共通のランダムな変動(ショック)
# 1. 発散過程のデータを生成します (ρ = 1.05)
explosive_data <- numeric(n)
explosive_data[1] <- shocks[1]
for (i in 2:n) {
explosive_data[i] <- 1.05 * explosive_data[i - 1] + shocks[i]
}
# 2. 単位根過程のデータを生成します (ρ = 1.0)
unit_root_data <- cumsum(shocks)
# 3. 定常過程のデータを生成します (ρ = 0.8)
stationary_data <- arima.sim(model = list(ar = 0.8), n = n, innov = shocks)
# --- グラフ描画 ---
# 描画デバイスを3行1列に分割します
par(mfrow = c(3, 1), mar = c(4, 4, 3, 2))
# プロット1: 発散過程
plot(explosive_data,
type = "l", col = "purple", lwd = 2,
main = "発散過程 (ρ > 1)",
xlab = "時間", ylab = "値",
las = 1
)
# 水平な基準線を追加します
abline(h = 0, col = "gray", lty = 2)
# プロット2: 単位根過程
plot(unit_root_data,
type = "l", col = "darkblue", lwd = 2,
main = "単位根過程 (ρ = 1)",
xlab = "時間", ylab = "", # 2番目以降のY軸ラベルは省略可
las = 1
)
abline(h = 0, col = "gray", lty = 2)
# プロット3: 定常過程
plot(stationary_data,
type = "l", col = "darkred", lwd = 2,
main = "定常過程 (|ρ| < 1)",
xlab = "時間", ylab = "", # Y軸ラベルを省略
las = 1
)
abline(h = 0, col = "gray", lty = 2)左から順に「発散過程」「単位根過程」「定常過程」のグラフを並べています。
- 左(発散過程): 時間の経過とともに、値が(指数関数的に)変化していく様子がわかります。
- 中央(単位根過程): 明確なトレンドはないものの、一度離れた水準に戻ることなくランダムに変動を続けています。平均に回帰する様子は見られません。
- 右(定常過程): 値がゼロ(平均値)の周りを安定して変動していることがわかります。大きなショックがあっても、いずれ平均値の方向に戻ろうとする力(平均回帰性)が働いているのが確認できます。
以上です。