Rの関数:breakpoints {strucchange}

Rの関数から breakpoints {strucchange} を確認します。

`breakpoints`関数について

breakpoints関数は、線形回帰モデルにおける1つまたは複数の未知の構造変化点（ブレークポイント）を推定するための関数です。構造変化点とは、データ系列の背後にある統計的性質が変化する時点を指します。

本関数は、指定された数の変化点によってデータを複数のセグメントに分割し、各セグメント内で計算される残差平方和（RSS）の合計を最小化するような変化点の位置を動的計画法を用いて特定します。

`breakpoints`関数の引数について

breakpoints.formulaメソッドの引数は以下の通りです。

library(strucchange)
args(getS3method("breakpoints", "formula"))

function (formula, h = 0.15, breaks = NULL, data = list(), hpc = c("none", 
    "foreach"), ...) 
NULL

formula:
モデルの構造を定義するformulaオブジェクトです。応答変数 ~ 説明変数1 + 説明変数2 のように記述します。例えば、y ~ x は、yをxで説明する線形回帰モデルを意味します。
h:
各セグメントに含まれるべき最小の観測数を指定するパラメータです。以下のいずれかの方法で指定します。
- 0から1の間の小数: 全観測数に対する割合で指定します。例えば、h = 0.15（デフォルト）は、全観測数の15%を最小セグメント長とすることを意味します。
- 整数: 最小の観測数を直接指定します。
この引数は、意味のある回帰分析を行うために、各セグメントが十分なデータ点を持つように保証する上で重要です。小さすぎるセグメントが生成されることを防ぎます。
breaks:
推定する変化点の数を整数で指定します。この引数がNULL（デフォルト）の場合、hの値に基づいて可能な最大の変化点の数が自動的に計算されます。明示的にbreaks = 2と指定すれば、2つの変化点を探索します。
data:
formulaで使用される変数が含まれるデータフレームやリストなどを指定します。
hpc:
計算を高速化するためのハイパフォーマンスコンピューティング（HPC）の利用方法を指定します。
- "none"（デフォルト）: 並列計算を行いません。
- "foreach": foreachパッケージを利用して並列計算を行います。このオプションを使用するには、foreachパッケージと、doParallelのような並列処理用バックエンドパッケージがインストールされている必要があります。データサイズが大きい場合に計算時間を短縮するのに有効です。
...:
内部で再帰残差を計算するために呼び出されるrecresid関数へ渡される、その他の引数を指定します。

シミュレーション

breakpoints関数を確認するためのシミュレーションを行います。

ここでは、2つの構造変化点を持つサンプルデータを作成し、breakpoints関数が正しく変化点を検出できるかを確認します。

1. サンプルデータの作成

3つの異なる期間（レジーム）で回帰直線の傾きが変化するようなデータを作成します。具体的には、80番目と140番目のデータ点で傾きが変わるように設定します。

# 構造変化分析のためのパッケージを読み込みます
library(strucchange)

# 再現性を確保するために乱数のシードを固定します
seed <- 20251022
set.seed(seed)

# シミュレーション用サンプルデータの作成
# データ全体の観測数を設定します
n <- 200

# 構造変化が発生する真の変化点を設定します
true_bp1 <- 80
true_bp2 <- 140
cat(paste("設定した真の変化点1:", true_bp1, "\n"))
cat(paste("設定した真の変化点2:", true_bp2, "\n\n"))


# 説明変数xを作成します
x <- 1:n

# 正規分布に従う誤差項を生成します
# この誤差項がデータのばらつきを生み出します
error <- rnorm(n, mean = 0, sd = 1)

# 応答変数yを格納するための空の数値ベクトルを用意します
y <- numeric(n)

# 3つの異なるレジームを持つデータを生成します
# レジーム1 (観測点 1 から true_bp1 まで)
# 切片が10、傾きが0.5の期間です
y[1:true_bp1] <- 10 + 0.5 * x[1:true_bp1] + error[1:true_bp1]

# レジーム2 (観測点 true_bp1 + 1 から true_bp2 まで)
# 傾きが-1.5に変化する期間です
# 連続性を保つため、前の期間の終点から計算を開始します
start_val_regime2 <- 10 + 0.5 * true_bp1
y[(true_bp1 + 1):true_bp2] <- start_val_regime2 - 1.5 * (x[(true_bp1 + 1):true_bp2] - true_bp1) + error[(true_bp1 + 1):true_bp2]

# レジーム3 (観測点 true_bp2 + 1 から n まで)
# 傾きが1.0に再度変化する期間です
start_val_regime3 <- start_val_regime2 - 1.5 * (true_bp2 - true_bp1)
y[(true_bp2 + 1):n] <- start_val_regime3 + 1.0 * (x[(true_bp2 + 1):n] - true_bp2) + error[(true_bp2 + 1):n]

# 作成したデータをデータフレームにまとめます
sim_data <- data.frame(x = x, y = y)

cat("--- サンプルデータの一部を確認 ---\n")
print(str(sim_data))

設定した真の変化点1: 80 
設定した真の変化点2: 140 

--- サンプルデータの一部を確認 ---
'data.frame':   200 obs. of  2 variables:
 $ x: int  1 2 3 4 5 6 7 8 9 10 ...
 $ y: num  11.4 11.1 11 12.1 12.7 ...
NULL

2. 作成したデータの可視化

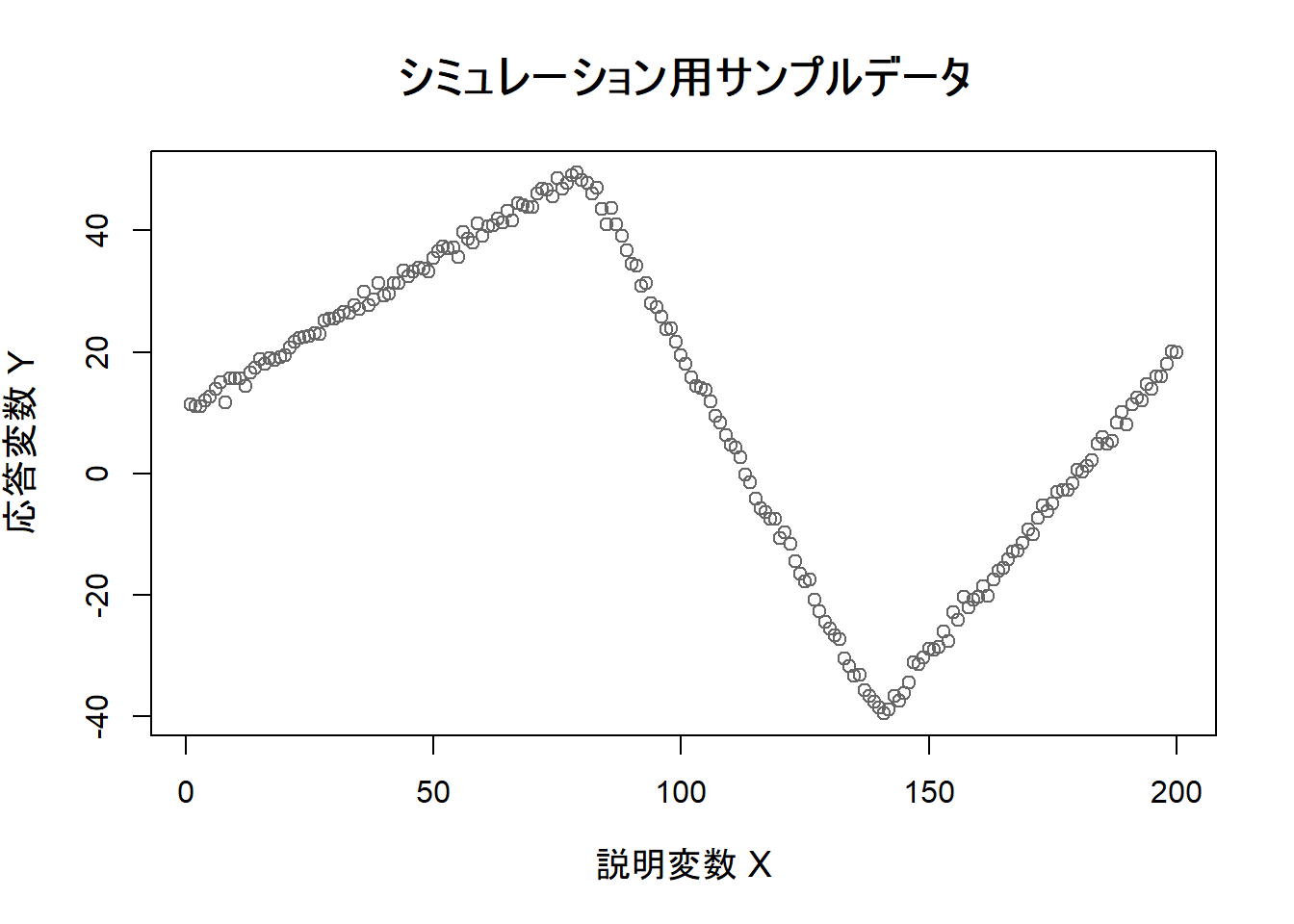
作成したデータを、散布図を描いて確認します。

# データをプロットして視覚的に確認します
plot(sim_data$x, sim_data$y,
  main = "シミュレーション用サンプルデータ",
  xlab = "説明変数 X",
  ylab = "応答変数 Y",
  pch = 1, col = "gray40",
  cex.main = 1.5, cex.lab = 1.2
)

xが80付近と140付近で、データの傾きが変化していることを見て取れます。

3. `breakpoints`関数の適用と結果の確認

作成したデータに対し、breakpoints関数を適用して構造変化点を推定します。

データ作成時に2つの変化点を設けましたので、breaks = 2と指定します。

hは、各セグメントが少なくとも観測数の10%（20点）を持つようにh = 0.1と設定します。

summary()関数を用いることで、推定された変化点の位置や、セグメントごとの回帰係数など、詳細な結果を確認できます。

# breakpoints関数による構造変化点の推定
# y ~ x という線形モデルを仮定し、2つの変化点を探索します
# h = 0.1 は、各セグメントが最低でも200 * 0.1 = 20 の観測点を持つことを意味します
bp_model <- breakpoints(y ~ x, data = sim_data, breaks = 2, h = 0.1)

# 結果の要約を表示します
cat("--- summary(bp_model)の確認 ---\n")
summary(bp_model)

--- summary(bp_model)の確認 ---

     Optimal (m+1)-segment partition: 

Call:
breakpoints.formula(formula = y ~ x, h = 0.1, breaks = 2, data = sim_data)

Breakpoints at observation number:
              
m = 1      112
m = 2   80 139

Corresponding to breakdates:
                 
m = 1       0.56 
m = 2   0.4 0.695

Fit:
                           
m   0       1       2      
RSS 82890.8 30039.1   173.1
BIC  1788.9  1601.8   586.4

「最適な変化点の位置」と「モデルの適合度」の2つの情報が示されています。

1. 最適な変化点の位置

Breakpoints at observation number:
              
m = 1      112
m = 2   80 139

Corresponding to breakdates:
                 
m = 1       0.56 
m = 2   0.4 0.695

このパートは、指定された変化点の数（m）ごとに、残差平方和（RSS）を最小化する最適な変化点の位置を示しています。

breakpoints関数を実行する際にbreaks = 2と指定したため、変化点が1つの場合（m = 1）と2つの場合（m = 2）の両方の結果が計算されています。

m = 1: もし、このデータに構造変化点が1つだけあると仮定した場合、最適な変化点の位置は112番目の観測点であることを示しています。
m = 2: もし、構造変化点が2つあると仮定した場合、最適な変化点の組み合わせは80番目と139番目の観測点であることを示しています。
Corresponding to breakdates: 上記の観測番号を、データ全体の長さ（このシミュレーションでは200）に対する割合（0から1の範囲）で示したものです。例えば、m = 2の場合、80番目は全体の40% (80/200)、139番目は全体の69.5% (139/200) の時点に相当します。

2. モデルの適合度

Fit:
                           
m   0       1       2      
RSS 82890.8 30039.1   173.1
BIC  1788.9  1601.8   586.4

このパートは、変化点の数（m）に応じた各モデルの適合度を評価するための統計指標を示しています。

m:
モデルに含まれる変化点の数を表します。
- m = 0: 変化点が無い、つまりデータ全体を1つの回帰直線で説明するモデル。
- m = 1: 変化点が1つのモデル。
- m = 2: 変化点が2つのモデル。
RSS (Residual Sum of Squares – 残差平方和):
モデルの予測値と実際の観測値の差（残差）の二乗和です。この値が小さいほど、モデルがデータによく当てはまっていることを意味します。
結果を見ると、変化点の数を増やすにつれて、RSSは 82890.8 → 30039.1 → 173.1 と減少しています。
BIC (Bayesian Information Criterion – ベイズ情報量規準):
同じくモデルの適合度を評価する指標です。RSSはモデルを複雑にする（変化点の数を増やす）ほど小さくなる傾向がありますが、複雑すぎるモデルは未知のデータに対する予測性能が低い「過学習」という問題を引き起こす可能性があります。
BICは、モデルの当てはまりの良さ（RSS）とモデルの複雑さ（パラメータ数）のバランスを考慮した指標です。このBICの値が最も小さいモデルが、統計的に最も良いモデルであると判断します。
今回の結果では、BICは 1788.9 → 1601.8 → 586.4 と減少しており、m = 2のモデルで最小値となっています。

結論

summaryの結果、特にBICの値に基づくと、「2つの変化点を持つモデル（m = 2）」が、変化点のないモデルや1つだけのモデルよりも統計的に優れていると結論付けられます。

さらに、その最適な変化点の位置は80番目と139番目であると推定されました。

今回のシミュレーションでは、80番目と140番目に構造変化を設定しましたので、breakpoints関数がデータの背後にある構造を捉えられたことが、この結果から確認できます。

4. 結果の可視化

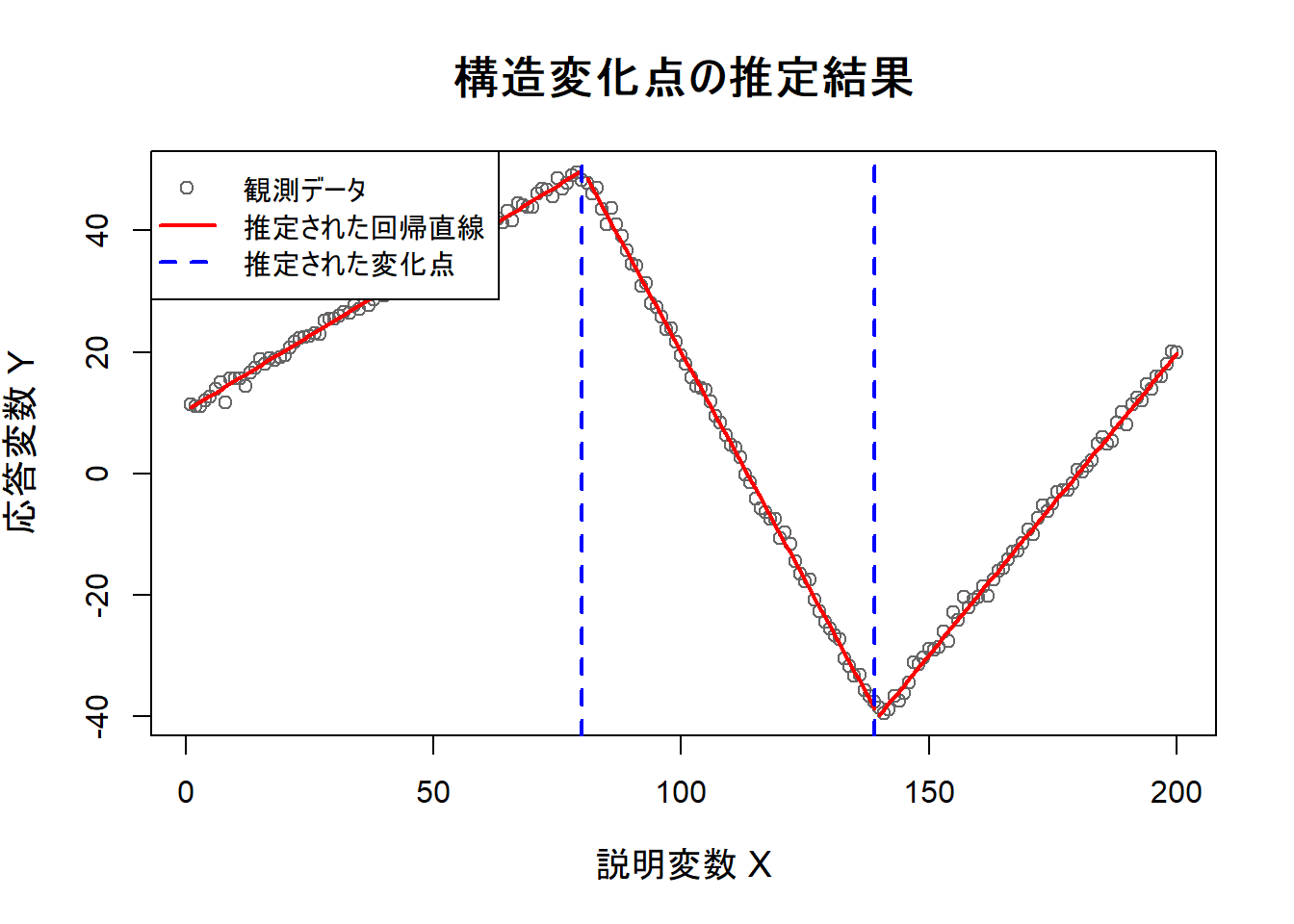
分析結果を可視化します。元のデータに、breakpoints関数によって推定されたセグメントごとの回帰直線と、変化点の位置を重ねてプロットします。

# 分析結果の可視化
# 1. 元のデータの散布図をプロットします
plot(sim_data$x, sim_data$y,
  main = "構造変化点の推定結果",
  xlab = "説明変数 X",
  ylab = "応答変数 Y",
  pch = 1, col = "gray40",
  cex.main = 1.5, cex.lab = 1.2
)

# 2. 推定されたセグメントごとの回帰直線を描画します
# 全ての観測点に対する推定値を取得します
fm <- fitted(bp_model, breaks = 2)
# 推定された変化点の位置を取得します
bpts <- bp_model$breakpoints
# データ全体の観測数を取得します
n <- nrow(sim_data)

# 変化点を基準にセグメントの区切りを定義します (データの開始点, 変化点, データの終了点)
all_bpts <- c(0, bpts, n)

# ループ処理を用いて、各セグメントの回帰直線を個別に描画します
for (i in 1:(length(all_bpts) - 1)) {
  # 現在のセグメントのインデックスを定義します
  segment_indices <- (all_bpts[i] + 1):all_bpts[i + 1]

  # 当該セグメントのxとyの推定値を用いて線を引きます
  lines(sim_data$x[segment_indices], fm[segment_indices], col = "red", lwd = 2)
}


# 3. 推定された変化点の位置に、青い破線の垂直線を引きます
abline(v = bp_model$breakpoints, col = "blue", lty = 2, lwd = 2)

# 4. 凡例を追加して、プロットの要素を説明します
legend("topleft",
  legend = c("観測データ", "推定された回帰直線", "推定された変化点"),
  col = c("gray40", "red", "blue"),
  lty = c(NA, 1, 2),
  pch = c(1, NA, NA),
  lwd = c(NA, 2, 2),
  bg = "white"
)

5. 信頼区間の確認

confint()関数を使用すると、推定された変化点の信頼区間を計算できます。

# 変化点の信頼区間の計算
# confint関数を用いて、95%信頼区間を計算します
ci_bp <- confint(bp_model, breaks = 2)

cat("--- confint(bp_model, breaks = 2)の出力 ---\n")
print(ci_bp)

--- confint(bp_model, breaks = 2)の出力 ---

     Confidence intervals for breakpoints
     of optimal 3-segment partition: 

Call:
confint.breakpointsfull(object = bp_model, breaks = 2)

Breakpoints at observation number:
  2.5 % breakpoints 97.5 %
1    79          80     81
2   138         139    140

Corresponding to breakdates:
  2.5 % breakpoints 97.5 %
1 0.395       0.400  0.405
2 0.690       0.695  0.700

1. 見出しと呼び出し情報

     Confidence intervals for breakpoints
     of optimal 3-segment partition: 

Call:
confint.breakpointsfull(object = bp_model, breaks = 2)

Confidence intervals for breakpoints of optimal 3-segment partition:
これから表示されるのが「最適な3セグメント分割における変化点の信頼区間」であることを示しています。2つの変化点（breaks = 2）を推定するということは、データを3つの異なる区間（セグメント）に分割することを意味します。
Call:
この結果を生成するために実行された関数呼び出しの詳細です。

2. 観測番号による信頼区間

Breakpoints at observation number:
  2.5 % breakpoints 97.5 %
1    79          80     81
2   138         139    140

2つの推定された変化点それぞれについて、95%信頼区間を観測番号で示しています。

breakpoints列:
summaryでも確認された、最適と推定された変化点の位置（80と139）です。
2.5 %列と97.5 %列:
それぞれ、95%信頼区間の下限値と上限値を示します。
行 1:
1番目の変化点についての結果です。
- 推定値は 80番目の観測点です。
- その95%信頼区間は 79番目から81番目まで です。これは、「もし同じ条件で何度もデータを取得し分析を繰り返した場合、真の変化点は95%の確率で79番目から81番目の間に含まれる」と解釈できます。
行 2: 2番目の変化点についての結果です。
- 推定値は 139番目の観測点です。
- その95%信頼区間は 138番目から140番目まで です。

この結果から、設定した両方の変化点(80番目と140番目)ともに95%信頼区間に含まれていることを確認できます。

3. データ全体における割合での信頼区間

Corresponding to breakdates:
  2.5 % breakpoints 97.5 %
1 0.395       0.400  0.405
2 0.690       0.695  0.700

こちらは、上記の観測番号をデータ全体の長さ（200）に対する割合（0から1の範囲）に換算して表示したものです。解釈は観測番号の場合と同じです。

1番目の変化点（推定値 0.40）の信頼区間は [0.395, 0.405] です。
2番目の変化点（推定値 0.695）の信頼区間は [0.690, 0.700] です。

以上です。

breakpoints関数について

breakpoints関数の引数について