Rの関数から dlmModReg {dlm} を確認します。
本ポストはこちらの続きです。

dlmModReg 関数
dlmModRegは、動的線形モデル(Dynamic Linear Model, DLM)の枠組みで、線形回帰モデルを構築するためのヘルパー関数です。
通常の線形回帰モデルでは、応答変数 y と説明変数 X の関係は、時間を通じて一定の回帰係数 β によってモデル化されます。
y_t = X_t * β + v_t
一方、dlmModRegを用いると、回帰係数 β が時間と共に変化する時変係数モデルを設定できます。このモデルでは、係数 β_t は各時点でランダムウォークに従って変動すると仮定されます。
- 観測方程式:
y_t = X_t * β_t + v_t,v_t ~ N(0, V) - 状態方程式:
β_t = β_{t-1} + w_t,w_t ~ N(0, W)
この関数は、説明変数 X、観測ノイズの分散 V、システムノイズの共分散行列 W などを指定することで、上記の構造を持つdlmオブジェクトを生成します。
特に、Wの値を調整することで、各回帰係数が時間でどの程度変動するかを制御できます。Wの対角成分が0であれば、その係数は時間不変(静的)となります。
dlmModReg 関数の引数
dlmModReg関数の引数について確認します。
library(dlm)
args(dlmModReg)function (X, addInt = TRUE, dV = 1, dW = rep(0, NCOL(X) + addInt),
m0 = rep(0, length(dW)), C0 = 1e+07 * diag(nrow = length(dW)))
NULLX: 説明変数を指定します。数値ベクトル、行列、またはts(時系列)オブジェクトを指定できます。t行目が時点tにおける説明変数の値(ベクトル)に対応します。addInt = TRUE: モデルに切片(インターセプト)項を追加するかどうかを指定する論理値です。デフォルトはTRUEですので、自動的に時変の切片項がモデルに追加されます。この場合、状態ベクトルの最初の要素が切片項の係数に対応します。dV = 1: 観測ノイズv_tの分散Vを指定するスカラー値です。デフォルトは1です。dW = rep(0, NCOL(X) + addInt): システムノイズw_tの共分散行列Wの対角成分を指定するベクトルです。各要素は、対応する回帰係数の時間的変動の大きさを表します。- ベクトルの長さは、係数の総数(説明変数の数
NCOL(X)+ 切片項の有無addInt)と一致させる必要があります。 -
dWのi番目の要素を0に設定すると、i番目の回帰係数は時間を通じて変化しない、静的な係数となります。 - デフォルトでは全ての要素が0ですので、通常の静的な線形回帰モデルが設定されます。
- ベクトルの長さは、係数の総数(説明変数の数
m0 = rep(0, length(dW)): 状態ベクトル(回帰係数ベクトルβ)の初期値β_0に関する事前分布の平均ベクトルを指定します。デフォルトでは、全ての係数の初期値の平均は0に設定されます。C0 = 1e+07 * diag(nrow = length(dW)): 状態ベクトルの初期値β_0に関する事前分布の共分散行列を指定します。デフォルトでは、10^7 と、非常に大きな分散を持つ対角行列が設定されます。これは、初期状態に関する情報がほとんどないことを示す「無情報事前分布」として機能します。
シミュレーション
ここからは、実際にdlmModRegを使って時変係数モデルのシミュレーションを行います。
1. サンプルデータの作成
まず、シミュレーションのためのサンプルデータを作成します。ここでは、時間と共に変動する切片項と、1つの説明変数の係数を持つモデルを考えます。
- 観測期間: 200時点
- 説明変数
x:sinカーブ - 時変係数:
-
β_{0,t}(切片): ランダムウォーク -
β_{1,t}(xの係数): ランダムウォーク
-
- 観測値
y:y_t = β_{0,t} + β_{1,t} * x_t + v_t
# 必要なパッケージをロードします
library(ggplot2)
library(dplyr)
library(tidyr)
# 再現性のために乱数シードを設定します
seed <- 20251001
set.seed(seed)
# シミュレーションの設定
time_len <- 1000
v_var_true <- 0.8 # 観測ノイズの真の分散
dw0_true <- 0.1 # 切片係数の変動の大きさ(システムノイズの分散)
dw1_true <- 0.2 # xの係数の変動の大きさ(システムノイズの分散)
# 説明変数 X を作成します (sinカーブ)
x_t <- sin(2 * pi * (1:time_len) / 50)
# 真の時変係数を作成します
# 切片項 (beta_0,t) はランダムウォークに従います
b0_true <- cumsum(rnorm(time_len, mean = 0, sd = sqrt(dw0_true)))
# xの係数 (beta_1,t) もランダムウォークに従います
b1_true <- cumsum(rnorm(time_len, mean = 0, sd = sqrt(dw1_true)))
# b1_true の平均を調整して、変動を分かりやすくします
b1_true <- b1_true - mean(b1_true) + 2
# 観測ノイズ v_t を作成します
v_t <- rnorm(time_len, mean = 0, sd = sqrt(v_var_true))
# 観測値 y_t を生成します
y_t <- b0_true + b1_true * x_t + v_t
# 作成したデータをデータフレームにまとめます
sim_data <- data.frame(
time = 1:time_len,
y = y_t,
x = x_t,
b0_true = b0_true,
b1_true = b1_true
)
# 生成した観測値と真の係数を確認します
cat("--- サンプルデータの一部を確認 ---\n")
print(head(sim_data))
# データをプロットして確認します
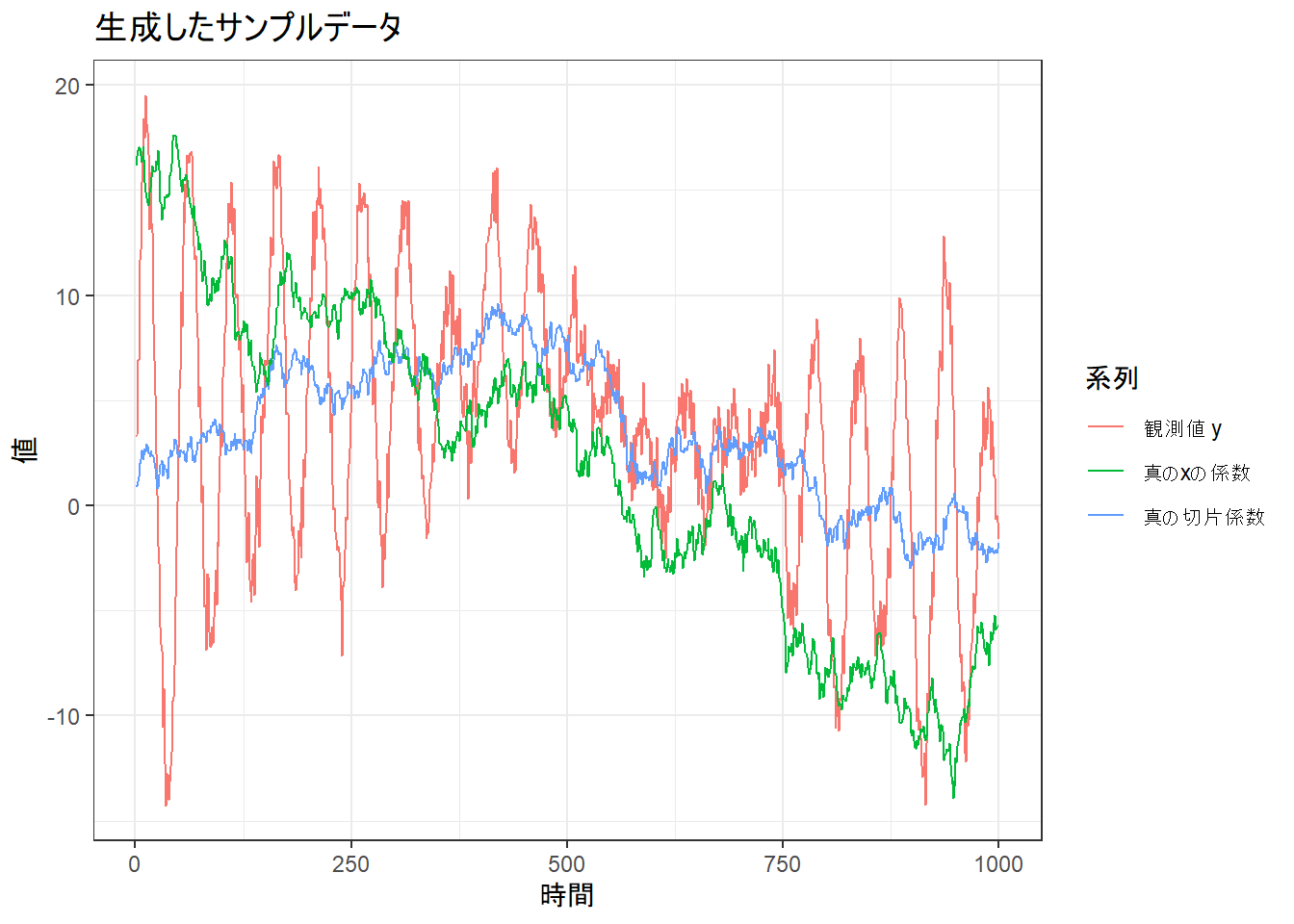
p_data <- ggplot(sim_data, aes(x = time)) +
geom_line(aes(y = y, color = "観測値 y")) +
geom_line(aes(y = b0_true, color = "真の切片係数")) +
geom_line(aes(y = b1_true, color = "真のxの係数")) +
labs(
title = "生成したサンプルデータ",
x = "時間",
y = "値",
color = "系列"
) +
theme_bw()
print(p_data)--- サンプルデータの一部を確認 ---
time y x b0_true b1_true
1 1 3.301301 0.1253332 0.9051667 16.17976
2 2 3.409633 0.2486899 0.9122749 16.60521
3 3 6.915383 0.3681246 1.1352395 16.89513
4 4 6.904902 0.4817537 1.3779340 17.03957
5 5 11.688579 0.5877853 2.0267528 17.04344
6 6 12.179919 0.6845471 2.1848028 16.639622. dlmModRegを用いたモデルの推定
次に、作成したサンプルデータ(y_t と x_t)を使って、dlmModRegでモデルを構築し、未知のパラメータ(観測ノイズ分散dVとシステムノイズ分散dW)を最尤法で推定します。その後、推定されたモデルを使って、フィルタリングとスムージングを行い、時変係数を推定します。
# 1. モデルの構造を定義する関数 (build function) を作成します
# この関数は、推定したいパラメータ(par)を引数に取り、dlmオブジェクトを返します
# 分散は正の値である必要があるため、対数を取った値を推定し、exp()で元に戻します
build_model <- function(par) {
dlmModReg(
X = x_t,
addInt = TRUE, # 切片項を追加します
dV = exp(par[1]), # 観測ノイズの分散
dW = exp(par[2:3]) # 状態ノイズの分散(切片項、xの係数)
)
}
# 2. 最尤推定 (MLE) でパラメータを推定します
# parmにはパラメータの初期値を設定します
mle_fit <- dlmMLE(y = y_t, parm = rep(0, 3), build = build_model)
# 推定結果を確認します
cat("推定の収束状況 (0は正常終了):", mle_fit$conv, "\n")
cat("推定された対数尤度:", -mle_fit$value, "\n\n")
# 推定されたパラメータ
dV_est <- exp(mle_fit$par[1])
dW_est <- exp(mle_fit$par[2:3])
cat("推定された観測ノイズの分散 (dV):", dV_est, "(真の値:", v_var_true, ")\n")
cat("推定されたシステムノイズの分散 (dW for b0):", dW_est[1], "(真の値:", dw0_true, ")\n")
cat("推定されたシステムノイズの分散 (dW for b1):", dW_est[2], "(真の値:", dw1_true, ")\n\n")
# 3. 推定されたパラメータを使って最終的なモデルを構築します
final_model <- build_model(mle_fit$par)
# 4. スムージングを実行して、時変係数を推定します
# dlmSmoothは、全期間のデータを使って各時点の状態を推定します
smoothed_res <- dlmSmooth(y = y_t, mod = final_model)
# 5. 結果を整形します
# スムージングされた状態(係数)の平均値を取得します
# dropFirst=TRUEは、t=0の初期状態を除外するためのオプションです
smooth_means <- dropFirst(smoothed_res$s)
colnames(smooth_means) <- c("b0_est", "b1_est")
# スムージングされた状態の分散共分散行列から、各係数の標準偏差を計算します
smooth_vars <- dlmSvd2var(smoothed_res$U.S, smoothed_res$D.S)
# sapplyの結果(p x T+1)を転置(T+1 x p)し、t=0の初期状態を除外します
# これにより、seは smooth_means と同じ T x p (200 x 2) の行列になります
se <- dropFirst(t(sqrt(sapply(smooth_vars, diag))))
# ======================
# 95%信頼区間を計算します
ci_upper <- smooth_means + 1.96 * se
ci_lower <- smooth_means - 1.96 * se
colnames(ci_upper) <- c("b0_upper", "b1_upper")
colnames(ci_lower) <- c("b0_lower", "b1_lower")
# 全ての推定結果と真の値を一つのデータフレームにまとめます
results_df <- data.frame(
time = 1:time_len,
b0_true = b0_true,
b1_true = b1_true,
b0_est = smooth_means[, "b0_est"],
b1_est = smooth_means[, "b1_est"],
b0_lower = ci_lower[, "b0_lower"],
b0_upper = ci_upper[, "b0_upper"],
b1_lower = ci_lower[, "b1_lower"],
b1_upper = ci_upper[, "b1_upper"]
)
# 6. 結果を可視化します
# 切片係数の比較
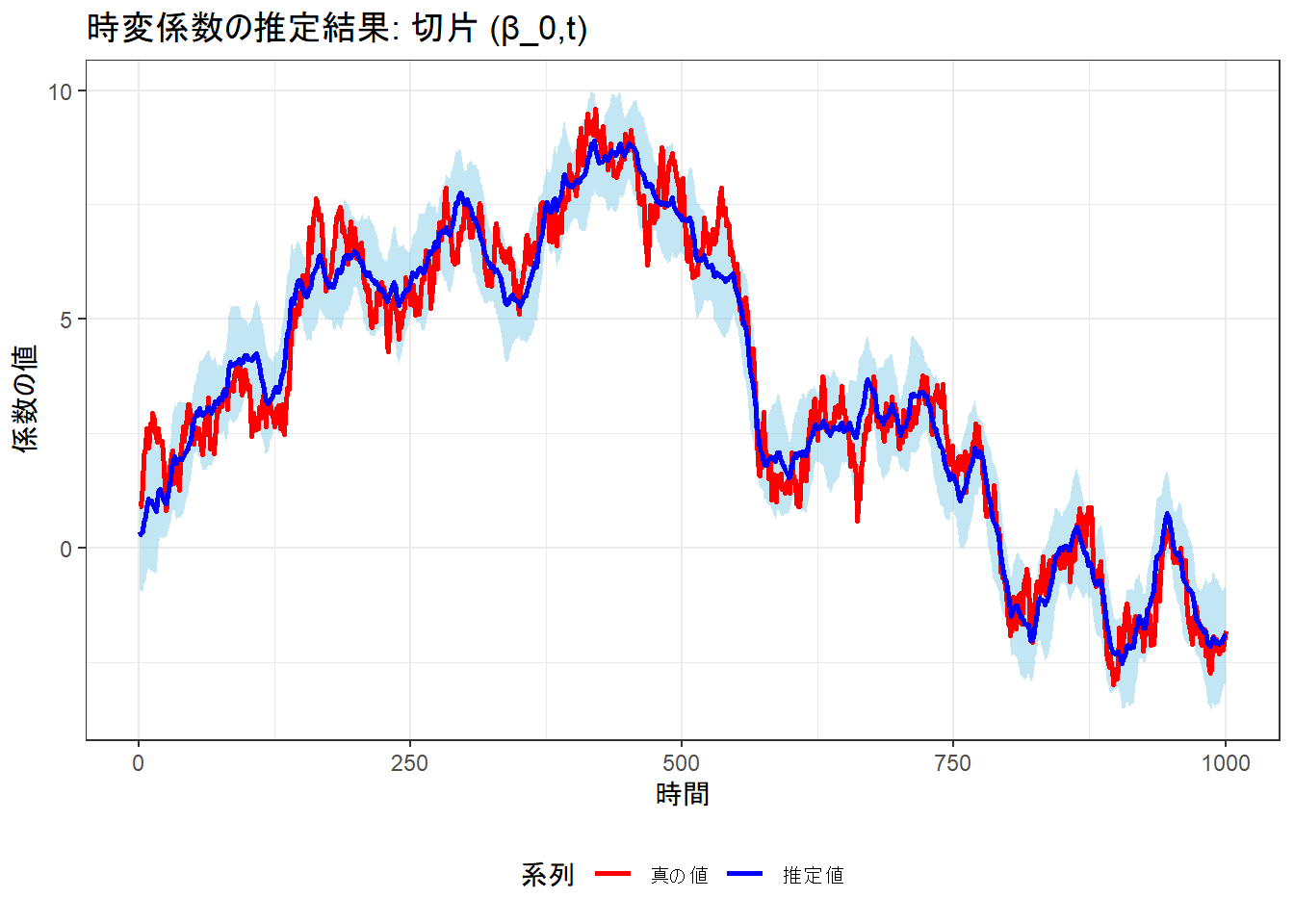
p_b0 <- ggplot(results_df, aes(x = time)) +
geom_ribbon(aes(ymin = b0_lower, ymax = b0_upper), fill = "skyblue", alpha = 0.5) +
geom_line(aes(y = b0_true, color = "真の値"), size = 1) +
geom_line(aes(y = b0_est, color = "推定値"), size = 1) +
scale_color_manual(values = c("真の値" = "red", "推定値" = "blue")) +
labs(
title = "時変係数の推定結果: 切片 (β_0,t)",
x = "時間",
y = "係数の値",
color = "系列"
) +
theme_bw() +
theme(legend.position = "bottom")
# xの係数の比較
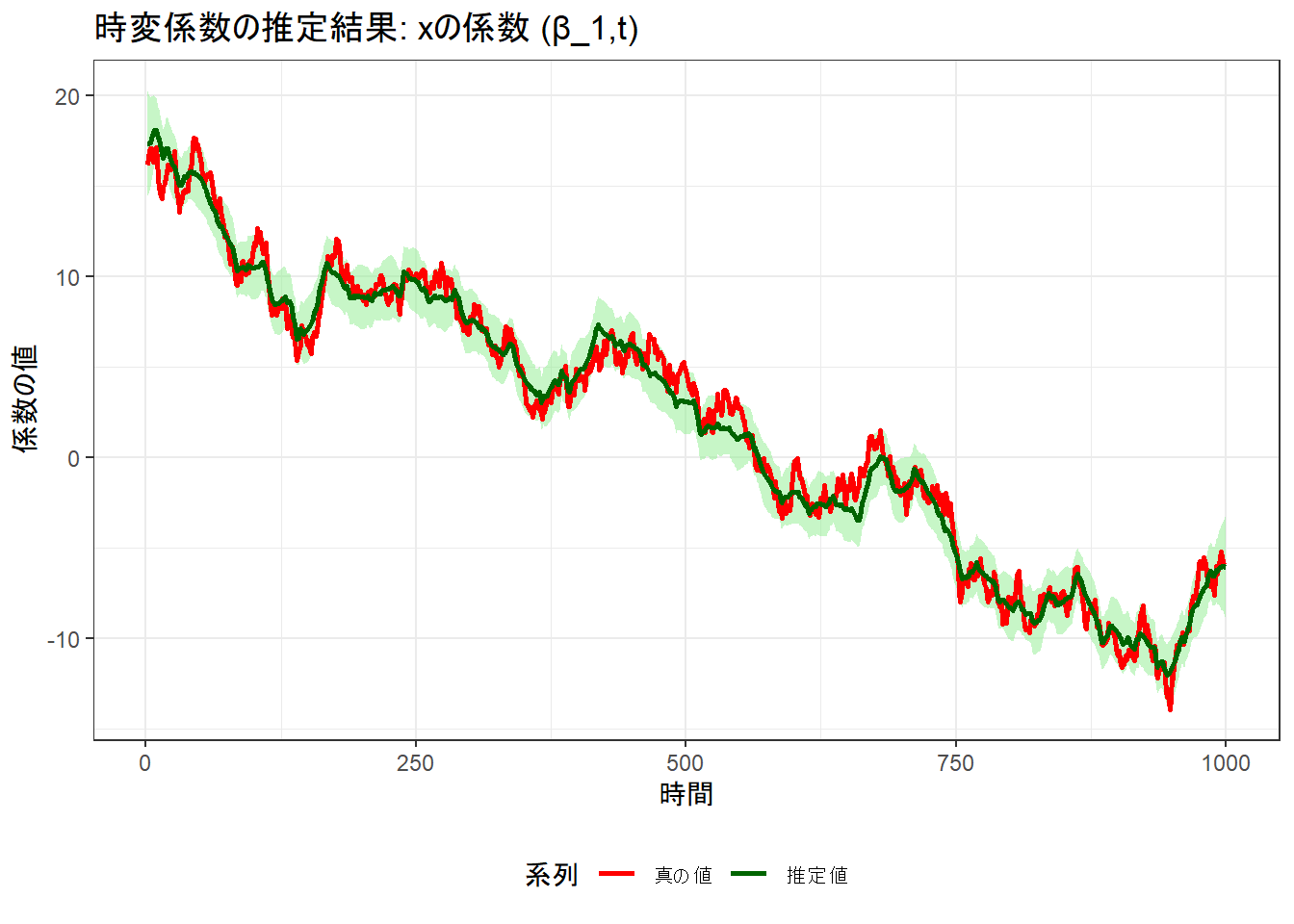
p_b1 <- ggplot(results_df, aes(x = time)) +
geom_ribbon(aes(ymin = b1_lower, ymax = b1_upper), fill = "lightgreen", alpha = 0.5) +
geom_line(aes(y = b1_true, color = "真の値"), size = 1) +
geom_line(aes(y = b1_est, color = "推定値"), size = 1) +
scale_color_manual(values = c("真の値" = "red", "推定値" = "darkgreen")) +
labs(
title = "時変係数の推定結果: xの係数 (β_1,t)",
x = "時間",
y = "係数の値",
color = "系列"
) +
theme_bw() +
theme(legend.position = "bottom")
# プロットを表示します
print(p_b0)
print(p_b1)推定の収束状況 (0は正常終了): 0
推定された対数尤度: -667.4645
推定された観測ノイズの分散 (dV): 0.8237561 (真の値: 0.8 )
推定されたシステムノイズの分散 (dW for b0): 0.0783322 (真の値: 0.1 )
推定されたシステムノイズの分散 (dW for b1): 0.1742766 (真の値: 0.2 )シミュレーション結果の解釈
観測値と予測値の比較
観測値 y と、推定されたモデルから得られる観測値の予測値(適合値)を比較します。
モデルによる観測値の推定値(適合値)は、スムージングによって得られた各時点の時変係数の推定値 β_t を使って、観測方程式 y_t = β_{0,t} + β_{1,t} * x_t に代入することで計算できます。
# 7. 観測値とモデルによる推定値の比較
# スムージングされた係数を用いて、観測値の推定値(適合値)を計算します
# y_hat_t = beta_0_est + beta_1_est * x_t
y_fitted <- smooth_means[, "b0_est"] + smooth_means[, "b1_est"] * x_t
# 残差(観測値 - 適合値)を計算します
residuals <- sim_data$y - y_fitted
# 比較のために、観測値、適合値、残差をデータフレームにまとめます
comparison_df <- data.frame(
time = sim_data$time,
observed = sim_data$y,
fitted = y_fitted,
residuals = residuals
)
cat("--- 観測値と適合値の一部を確認 ---\n")
print(head(comparison_df))
# 観測値と適合値をプロットして比較します
p_fit <- ggplot(comparison_df, aes(x = time)) +
geom_point(aes(y = observed, color = "観測値"), alpha = 0.6, size = 2) +
geom_line(aes(y = fitted, color = "適合値"), size = 1) +
scale_color_manual(values = c("観測値" = "gray50", "適合値" = "red")) +
labs(
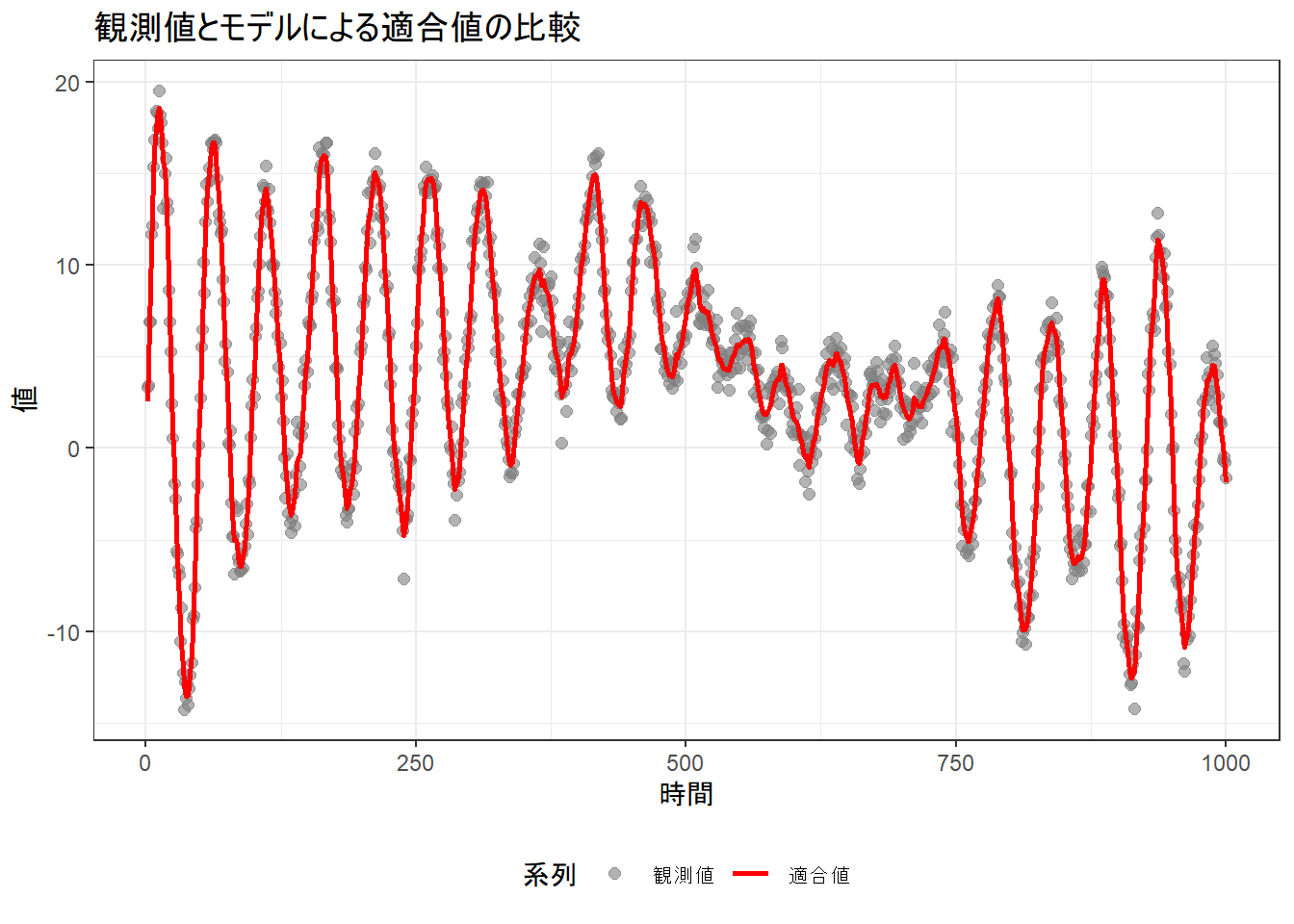
title = "観測値とモデルによる適合値の比較",
x = "時間",
y = "値",
color = "系列"
) +
theme_bw() +
theme(legend.position = "bottom")
# 残差をプロットして、モデルの当てはまり具合を確認します
p_residuals <- ggplot(comparison_df, aes(x = time, y = residuals)) +
geom_point(alpha = 0.7, color = "dodgerblue") +
geom_hline(yintercept = 0, linetype = "dashed", color = "red") +
labs(
title = "残差のプロット",
x = "時間",
y = "残差 (観測値 - 適合値)"
) +
theme_bw()
# プロットを表示します
print(p_fit)
print(p_residuals)--- 観測値と適合値の一部を確認 ---
time observed fitted residuals
1 1 3.301301 2.543878 0.7574233
2 2 3.409633 4.606852 -1.1972187
3 3 6.915383 6.734023 0.1813591
4 4 6.904902 8.746297 -1.8413956
5 5 11.688579 10.918115 0.7704643
6 6 12.179919 12.831681 -0.6517616- 観測値と適合値の比較プロット Figure 4 :
- 灰色の点が実際の観測値
yで、赤い線がモデルによって推定された適合値です。 - 赤い線が灰色の点の中心を追従していることがわかります。
- 灰色の点が実際の観測値
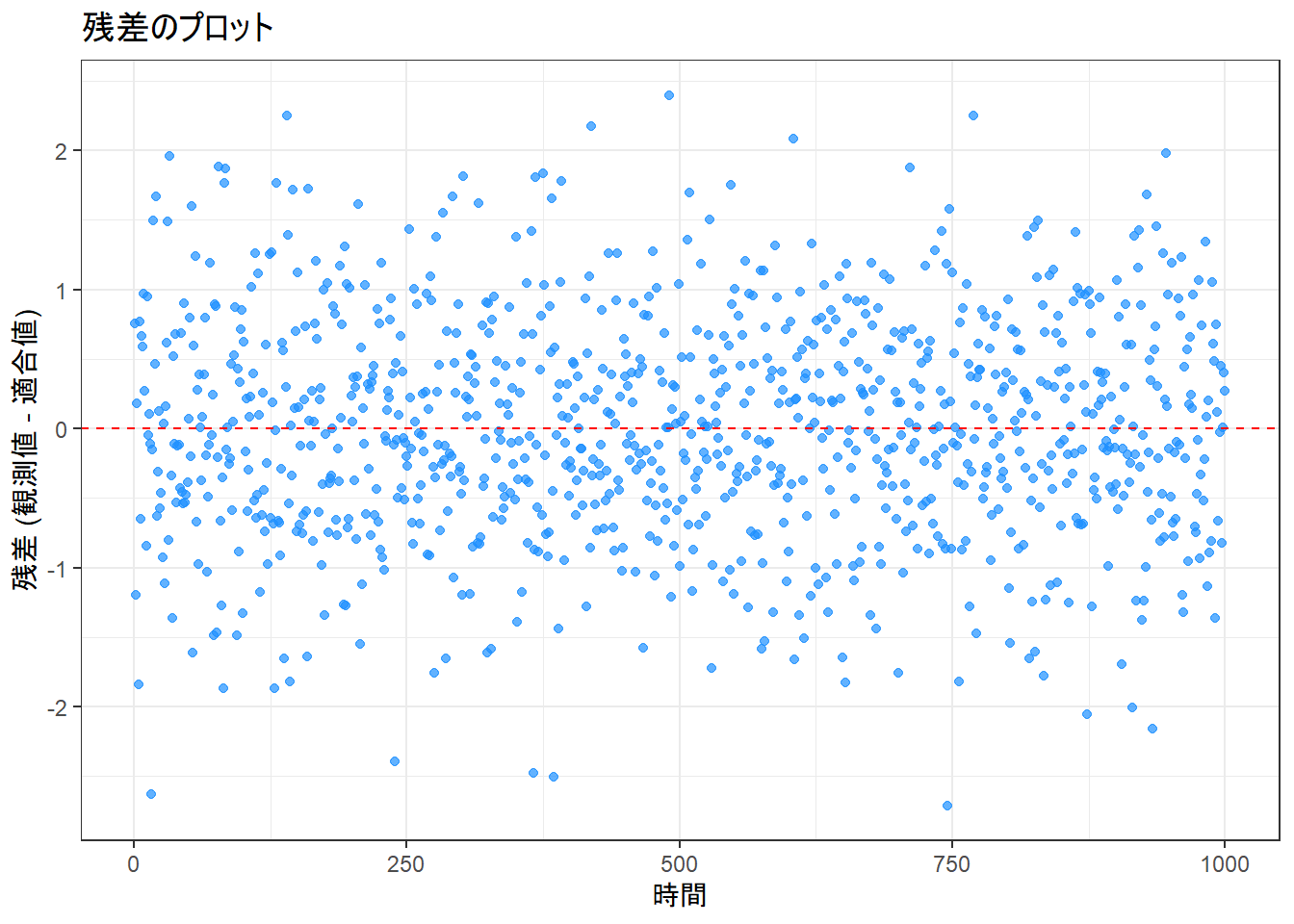
- 残差のプロット Figure 5 :
- 残差は「観測値 – 適合値」であり、モデルで説明しきれなかった部分(ノイズ成分)に相当します。
- このプロットでは、残差が特定の傾向(例えば、時間と共に増加/減少する、周期的なパターンを持つなど)を持たず、赤い破線で示された0の周りでランダムに分布しているように見えます。
以上です。